비선형 자료 구조
자료 사이의 전후 관계가 1:1 이 아닌 구조
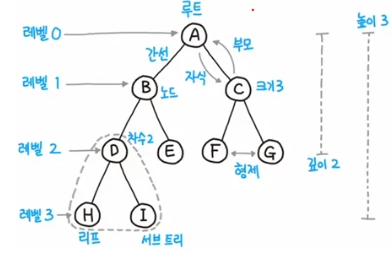
Tree
회로
cycle가 없는 연결된 그래프
이진 트리
모든 노드의 차수
자식노드 개수가 2 이하로만 있는 이루어진 트리
- 종류
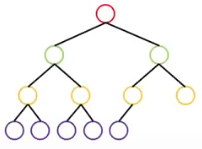
- 완전 이진 트리
마지막 레벨을 제외한 모든 레벨에서 노드가 꽉차 있는 이진 트리
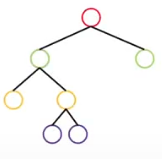
- 정 이진 트리
모든 노드의 차수가 0 또는 2인 이진 트리
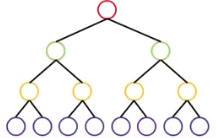
- 포화 이진 트리
모든 내부의 차수가 0 또는 2인 이진트리
그림 출저 : https://seen-ma.tistory.com
+ 완전 이진 트리
배열 구현이 간편함.
- 루트 노드의 인덱스 = 0
레벨이 낮은 노드부터 왼쪽 노드부터 인덱스 부여부모 노드의 인덱스가 n 일 때,
1 ) 왼쪽 자식 노드의 인덱스 : 2n + 1
2 ) 오른쪽 자식 노드의 인덱스 : 2(n + 1)
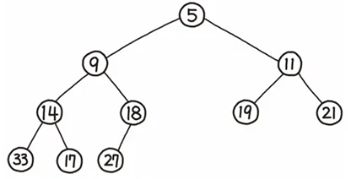
이진 트리 구조 순회
- 전위 순회
- 루트 -> 왼쪽 부분 트리 -> 오른쪽 부분 트리 순
- 루트로 부터 값을 누적 시킬 때 주로 사용
- 5 9 14 33 17 18 27 11 19 21
- 중위 순회
- 왼쪽 부분 트리 -> 현재 노드 -> 오른쪽 부분 트리 순
- 수식 트리 구조 , 상태 판단을 하는 경우 주로 사용
- 33 14 17 9 18 27 5 11 19 21
- 후위 순회
- 왼쪽 부분 하위 트리 -> 오른쪽 하위 트리 -> 현재 노드 순
- 말단 노드 삭제 , 말단 노트로 부터 값을 누적하는 경우 주로 사용
- 33 17 14 27 18 9 19 21 11 5
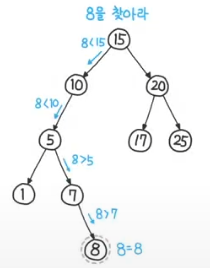
이진 탐색 트리
다음의 규칙을 만족하는 이진 트리
- 모든 노드는 비교할 수 있는 키 값을 가지며 , 값들은 전순서가 있다.
- 모든 노드의 왼쪽 자손 노드들은 부모 노드보다 작은 키를 가지는 노드만 존재한다.
- 모든 노드의 오른쪽 자손 노드들은 부모 노드보다 큰 키를 가지는 노드만 존재한다.
- 이진 탐색 트리의 부분 트리는 항상 이진 탐색 트리 구조이다.
- 구현
- 노트 탐색·삽입
루트 노드부터 시작하여 자손 노드가 없을 때 까지 데이터 비교- 노드 제거
- 자손 노드가 없을 경우 : 노드 삭제
- 자손 노드가 하나만 있는 경우
현재 노드의 부모 노드와 자손 노드를 연결한 뒤 노드 삭제
즉, 하위 부분 트리를 한 레벨씩 올림.
- 자손 노드가 두 개 있는 경우
우측 자손 트리에서 최솟값을 가지는 말단 노드를 찾아
해당 말단 노드의 데이터와 삭제할 노드의 데이터를 교체 이후 해당 말단 노드 삭제
- 시간 복잡도
- 트리가 균형 상태일시 탐색·삽입·삭제 시간 O(log n)
- 최악일 시 O(n)
이진 힙 트리
다음의 규칙을 만족하는 이진 트리
- 부모 노드의 값이 자식 노드의 값보다 항상 크다
max heap- 부모 노드의 값이 자식 노드의 값보다 항상 작다
min heap
- 구현
- 노드 탐색
루트 노드만 탐색
일반적인 트리 순회 · 노드 탐색은 고려하지 않음.- 노드 삽입
완전 이진 트리를 유지하도록 마지막 레벨의 가장 우측 노드 자리에 삽입한 뒤
재귀적으로 부모 노드와 비교하여 힙 속성을 만족하도록 노드간 데이터 교체- 노드 제거
마지막 레벨의 가장 우측 노드와 루트 노드의 데이터를 교체한 다음,
힙 속성을 만족할 때까지 재귀적으로 자식 노드와 데이터를 비교하여 교체
- 시간 복잡도
노드의 삽입/제거의 시간 복잡도는 O(log n)이다.
시간 복잡도가 트리의 높이에만 의존
완전 이진 트리 구조를 항상 유지해야 한다.
priority queue 를 구현 하는데 사용한다.
+ STL priority queue
우선 순위가 높·낮은 순으로 요소를 인출하는 큐 구조
- STL priority_queue<_Ty, _Container, _Pr>
- Container = vector<_Ty>
기본- _Pr = less<_Ty>
우선 순위를 비교하기 위해 비교 연산자가 존재한다.
< : max heap 구조가 나타난다.
> : min heap 구조가 나타난다.
AVL Tree
대표적 자가 균형 이진 탐색 트리
- 모든 노드에서 왼쪽 자손 트리의 높이와 오른쪽 자손 트리의 높이 차이가 1이하인 트리구조
- 이상적인 상황, 최악의상황 모두 노트 탐색/삽입/제거의 시간 복잡도가 O(log n)
- 노드 삽입/제거 시에 부분 트리를 회전함으로써 균형 유지
각 노드 별 balance factor 계산
균형이 잘 잡힌 트리이지만 다른 자가 균형 이진 트리에 비해 삽입/제거가 느리다.
Red-Black Tree
다음 조건을 만족하는 대표적 자가 균형 이진 트리
- 모든 노드는 레드 아니면 블랙이다.
- 모든 NIL 리프 노드는 블랙이다.
- 레드 노드의 자식 노드는 언제나 블랙이다.
블랙 노드만이 레드 노드의 부모가 될 수 있다.
따라서 루트 노드는 반드시 블랙이다.- 임의의 한 노드에서 널 리프 노드까지 도달하는 모든 경로에는
널 리프 노드를 제외하고 항상 같은 수의 블랙 노드가 있다.
- 균형을 유지하기 위한 규칙들을 만족하기 위해 노드/삽입 제거시 부분 트리를 회전
노드 삽입·삭제 case 에 따른 회전 규칙이 매우 다양하다.- 구현이 매우 까다롭지만 일반적인 경우에서 높은 성능을 보인다.
- STL 의 set , map 클래스가 red-black tree 에 기반하여 구현 되어 있다
- 균형이 적절하게 잡히므로 다른 자가 균형 이진 트리에 비해 삽입·제거가 빠르다.
- 시간 복잡도
- 균형 유지 O(1)
- 노드 탑색·삽입·삭제 O(log n)
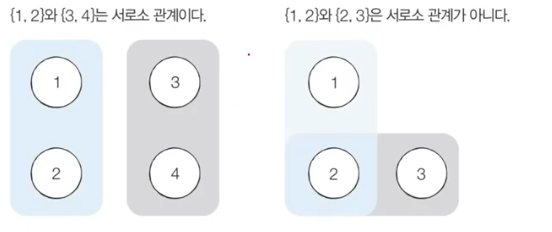
서로소 집합 구조
상호 배타적으로 이루어진 집합을 효율적으로 표현하기 위한 구조
- union 연산 : 서로 다른 두개의 집합을 하나의 집합으로 병합하는 연산
항상 작은 트리를 큰 트리 루트에 붙이는 형태로 유니온 연산을 구현한다.최적화- Find 연산 : 하나의 원소가 어떤 집합에 속해 있는지 판단.
O(1)
루트 노드를 찾을 때 까지 방문한 노드들의 부모 노드를 루트 노드로 갱신한다.최적화, 경로 압축
- 구현
template<typename T> class DisjointSet { public : struct Set { T Data; Set* Parent; }; static void Union(Set* a, Set* b) { if (a == b) return; Set* pa = Find(a); Set* pb = Find(b); if (pa == pb) return; pb->Parent = a; } static void Find(Set* a) { if (a == a->Parent) return a; return a->Parent = Find(a->Parent); // 경로 압축 } }
그래프
정점과 각 정점을 연결하는 변으로 구성되는 자료구조
- 각각의 변
간선은 가중치를 가질 수 있다.- 트리와는 다르게 시작 정점의 위치가 고정적이지 않을 수 있다.
- 변으로 연결된 정점들 사이에 순환이 가능하다.
- 행렬 또는 연결 리스트로 구현 가능하다.