문제

너비가 1인 기둥들의 양의 정수인 높이들이 주어질 때, 비가 온 후 기둥들 사이에 담길 물의 양을 계산하시오.

Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Example 2:

Input: height = [4,2,0,3,2,5]
Output: 9

---

풀이

많이 어려웠고, 도저히 생각이 안나서 책을 참고했다.
두 가지 풀이에 대해 이해한 것을 바탕으로 설명해 보도록 하겠다

1. Two-Pointer를 이용한 풀이.

이 문제를 풀기 위해서는 아래와 같은 변수들이 필요하다.

• left: 왼쪽에서부터 움직이고 있는 변수.
• right: 오른쪽에서부터 움직이고 있는 변수.
• max_height.left: left가 지나오면서 가장 높인 기둥의 높이.
• max_height.right: right가 지나가면서 가장 높은 기둥의 높이.

이 문제는 코드를 보면서 설명하는 것이 이해가 더 잘 갈 것이다.

from collections import namedtuple

class Solution:
    def trap(self, height: List[int]) -> int:
        
        #예외 처리
        if not height:
            return 0

        #변수 초기화
        volume = 0
        left, right = 0, len(height) - 1
        max_height = namedtuple('max_height', 'left right')
        max_height.left, max_height.right = height[left], height[right]
		
        #가장 높은 기둥에 도달할 때까지 while문을 반복.
        while left < right:
            
            #왼쪽과 오른쪽의 최고 높이 갱신
            max_height.left = max(max_height.left, height[left])
            max_height.right = max(max_height.right, height[right])
            
            #한 번에 한 쪽씩만 움직이면서 물 더하기.
            if max_height.left <= max_height.right:
                volume += max_height.left - height[left]
                left += 1
            else:
                volume += max_height.right - height[right]
                right -= 1

        return volume

일단, 핵심은 while문 안이다. while문의 종료 조건은 left == right이다.
즉, 반복문의 매 회마다 max_height.left와 max_height.right의 값을 갱신한 후,
두 값을 비교하여 한쪽만 volume을 계산해 나간다.

이렇게 하면, max_height.left와 max_height.right중 어느 한 쪽이라도 낮은 쪽의 빗물은 volume에 더해지면서 이동할 것이므로, 결국 두 포인터 모두 기둥 중 가장 높은 기둥에서 만나게 된다.

2. Stack을 이용한 풀이.

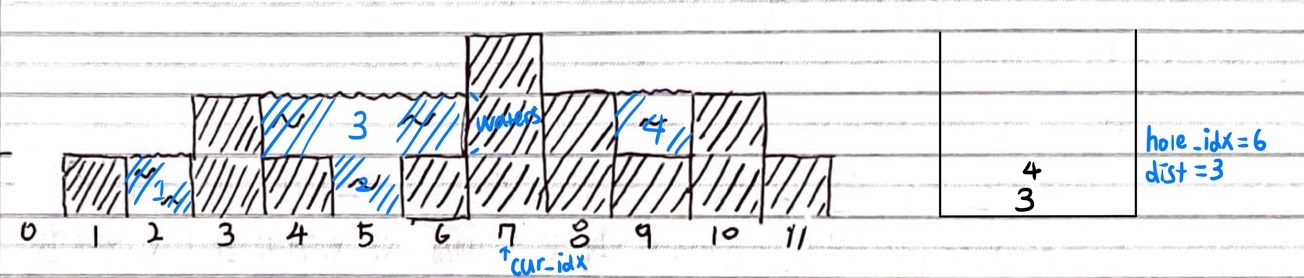
이번엔 Stack을 이용한 풀이이다. 이번 풀이는 하나의 포인터만 사용한다.

class Solution:
    def trap(self, height: List[int]) -> int:
        idx_stack = []
        volume = 0
        
        # 한 방향으로 진행한다.
        for cur_idx in range(len(height)):
            
            # stack이 비어있지 않고, 현재의 기둥 높이가 이전 기둥의 높이보다 높은 경우.
            while idx_stack and height[cur_idx] > height[idx_stack[-1]]:
                hole_idx = idx_stack.pop()

                if not idx_stack:
                    break

                dist = cur_idx - idx_stack[-1] - 1
                waters = min(height[cur_idx], height[idx_stack[-1]]) - height[hole_idx]

                volume += dist * waters

            idx_stack.append(cur_idx)

        return volume