[알고리즘] 시간 복잡도

알고리즘 문제를 풀다보면 해답을 찾는 것도 중요하지만좀 더 효율적으로 문제를 해결하는 방법에 대해 고민하게 된다.

이럴 때 필요한 것이 시간 복잡도를 고려하는 것이다.

시간 복잡도를 고려한다는 것은 '입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는가?'라는 뜻이다.

그리고 이 시간 복잡도는 주로 빅-오 표기법을 사용해 나타낸다.

Big-O 표기법

시간 복잡도를 표기하는 방법

• Big-O(빅-오) => 상한 점근
• Big-Ω(빅-오메가) => 하한 점근
• Big-𝜃(빅-세타) => 그 둘의 평균
• 위 세 가지 표기법은 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법이다.

가장 자주 사용되는 표기법

• 빅오 표기법은 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있다.
• "최소한 특정 시간 이상이 걸린다" 혹은 "이 정도 시간이 걸린다"를 고려한는 것보다 "이 정도 시간까지 걸릴 수 있다"를 고려해야 그에 맞는 대응이 가능하다.

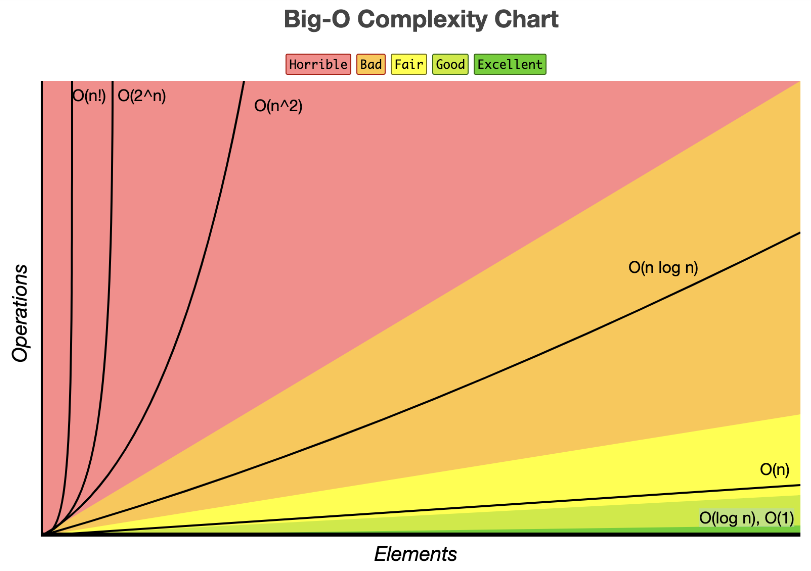
Big-O 표기법의 종류

1. O(1)
2. O(n)
3. O(log n)
4. O(n^2)
5. O(2^n)

O(1)

O(1)은 일정한 복잡도(constant complexity)라고 하며, 입력값이 증가하더라고 시간이 늘어나지 않는다.

• 다시 말해 입력값의 크기와 관계 없이, 즉시 출력 값을 얻어낼 수 있다는 말이다.

O(1)의 시간 복잡도를 가진 알고리즘

public int O_1_algorithm(int[] arr, int index) {
  return arr[index];
}

int[] arr = new int[]{1,2,3,4,5};
int index = 1;
int results = O_1_algorithm(arr, index);
System.out.println(results); // 2

O(n)

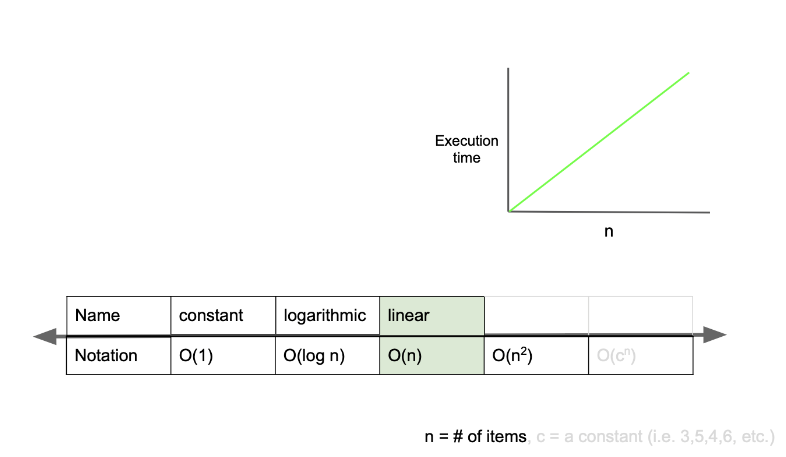
O(n)은 선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.

O(n)의 시간 복잡도를 가진 알고리즘

public void O_n_algorithm(int n) {
	for (int i = 0; i < n; i++) {
	// do something for 1 second
	}
}

public void another_O_n_algorithm(int n) {
	for (int i = 0; i < n * 2; i++) {
	// do something for 1 second
	}
}

another_O_n_algorithm에서 입력 값이 1 증가할 때마다 코드의 실행 시간은 2초씩 증가한다. 하지만 표기법은 O(2n)이 아닌 O(n)으로 동일하다. 그 이유는 입력 값이 커질 수록 계수의 의미가 점점 퇴색되기 때문에, 같은 비율로 증가하고 있다면 O(n)으로 표기한다.

O(log n)

O(log n)은 로그 복잡도(logarithmic complexity)라고 부르며, Big-O 표기법 중 O(1) 다음으로 빠른 시간 복잡도를 가진다.

자료구조의 BST(Binary Search Tree)가 탐색 하면 할수록 경우의 수가 계속 절반으로 줄어들기 때문에 O(log n)의 시간 복잡도를 가진 알고리즘이라고 할 수 있다.

O(n^2)

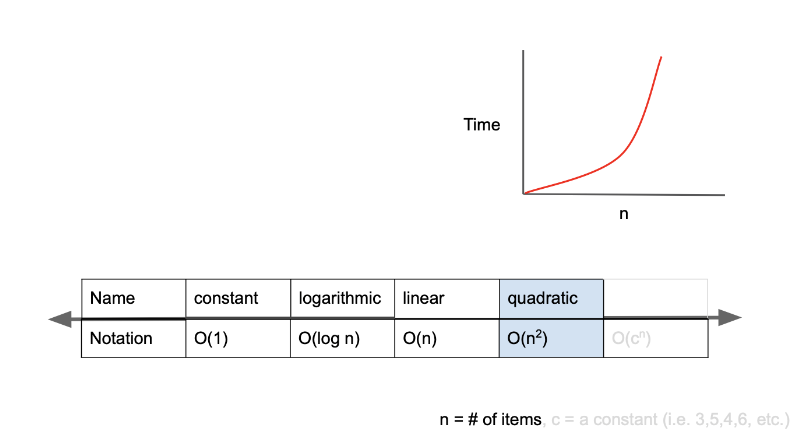
O(n^2)은 2차 복잡도(quadratic complexity)라고 부르며, 입려값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.

O(n^2)의 시간 복잡도를 가진 알고리즘

public void O_quadratic_algorithm(int n) {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			// do something for 1 second
		}
	}
}

public void another_O_quadratic_algorithm(int n) {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
        	for (int k = 0; k < n; k++) {
            	// do something for 1 second 
			}
		}
	}
}

O(n)과 마찬가지로 O(n^2)도 모두 O(n^2)로 표기한다.

O(2^n)

O(2^n)은 기하급수적 복잡도(exponential complexity)라고 부르며, Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.

O(2^n)의 시간 복잡도를 가진 알고리즘

public int fibonacci(int n) {
	if (n <= 1) {
    	return 1;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

재귀로 구현하는 피보나치 수열은 O(2^n)의 시간 복잡도를 가진 대표적인 알고리즘이다.