
Neural Network의 목적
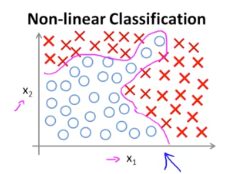
우리는 두개 혹은 그 이상의 결과값을 분류(Classification)하기 위해 Logistic Regression을 사용하였습니다.
그런데 만약 위와 같이 'non-linear'한 Decision Boundary가 필요한 경우 가설함수가 복잡해져 기존의 Logistic Regression으로는 연산이 어려웠지만 Neural Network로 이를 해결할 수 있었습니다.
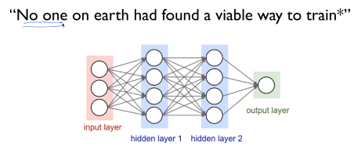
우리가 Neural Network도 정규화된 Logistic Regression을 기반으로 그 목표는 최대한 실제값에 가깝게 잘 예측하는 것입니다.
이를 위해선 Neural Network를 학습시켜야 하고, 결국 학습시킨다는 말은 실제값과 예측값의 오차인 Cost(비용)을 최소화 한다는 것입니다.
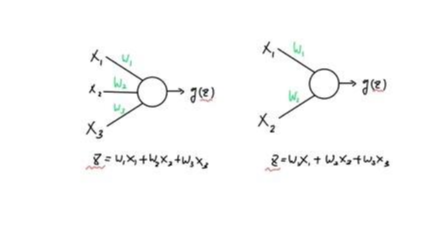
우리가 익히 아는 Gradient Descent Algorithm을 Neural Network에 이용하여 Cost를 최소화해보겠습니다.
Neural Network 속 하나의 Unit은, Input과 가중치 W 가 곱해져 Z가 만들어집니다. 이를 sigmoid 함수 g에 넣어 도출된 결과값 g(Z)를 다음 Layer로 보냅니다.
최종적인 목표는 Cost를 최소화시키는 Neural Network 내의 모든 Unit의 가중치 W 를 찾는 것입니다.
이를 Neural Network를 최적화한다고 표현합니다.
Forward Propagation
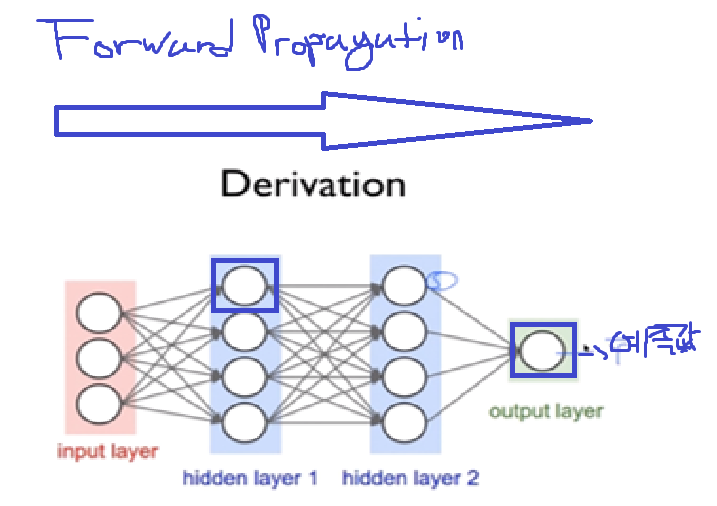
본격적으로 Back Propagation을 알아보기 전, 위 Neural Network에서 Layer 2의 첫번째 Unit을 최적화하며, Forward Propagation의 문제점을 알아보겠습니다.
우선 Cost를 구하기 위해서는 Neural Network의 예측값을 구해야합니다.
- 따라서 Output Layer에서의 최종적인 예측값을 구하기 위해서는, Layer 3의 4개의 Unit이 각각의 g(z)값을 Output Layer에 보내줘야 합니다.
- 근데 이 layer 3의 g(z)을 각각 구하기 위해서는, Layer 2의 unit들은 'Input Layer'에서 받은 Input으로 g(z)값 을 계산해서 Layer 3에 보내줘야합니다.
- 이렇게 구한 예측값을 실제값에서 빼면 Cost를 구할 수 있게 됩니다.

그러면 현재 우리는 Gradient Descent Algorithm을 이용하고 있으므로, 계산한 Cost의 미분값에 learning rate를 곱하여 가중치 W에서 뺌으로써 한번의 갱신이 이뤄집니다.
근데 여기서 끝이 아닙니다! 우리는 한번의 갱신을 한것이지 Cost를 최소화하기 위해 이 짓을 적게는 몇 백번, 많게는 몇 천번을 연산해줘야 합니다.
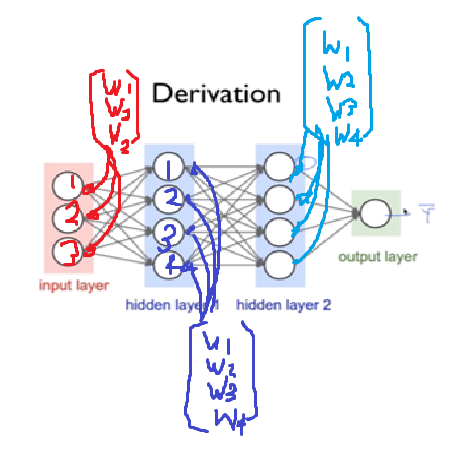
백보 양보해서 하나의 Unit에서 최적화 하는데 성공했습니다. 그러나 우리는 이 짓을 Neural Network에 있는 나머지 Unit들에 대해서 똑같이 다 해줘야 합니다.
만약 우리가 사용하려는 Neural Network의 Layer가 100개였다면 이러한 방식은 연산량이 무한대에 가까울 것이며 불가능합니다.
이처럼 Forward Propagation은 Neural Network가 커질수록 최적화를 위한 연산량이 기하급수적으로 늘어나게 됩니다.
한동안 전문가들은 이러한 문제에 봉착하여 한동안 연구가 진전되지 못하다가 나오게 된것이 바로 Back Propagation입니다.
Back Propagation
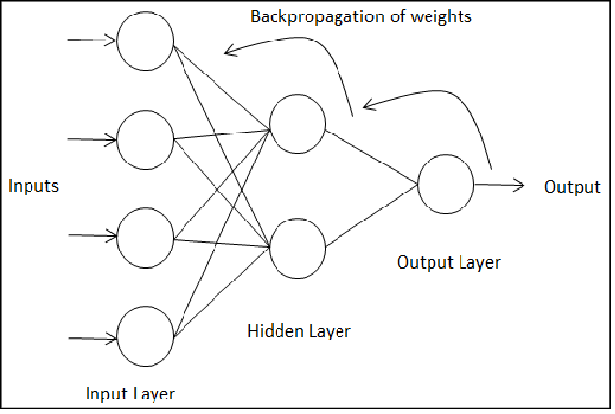
'Back Propagation' 는 Output Layer 직전의 Layer부터 최적화합니다.
미리 말하고 싶은 것은 'Back Propagation'도 Gradient Descent를 이용합니다. 즉 앞서 배웠던 Forward Propagation처럼 Cost를 구하여 W를 여러번 갱신하여 최적화합니다.
다만 그 차이는 'Forward Propagation'은 한번의 갱신을 위한 Cost를 구하는데 비효율적으로 많은 연산을 필요로 합니다.
그러나 'Back Propagation'에서는 최적화의 순서를 달리하여 몇번의 연산만으로 Cost를 구할 수 있습니다.
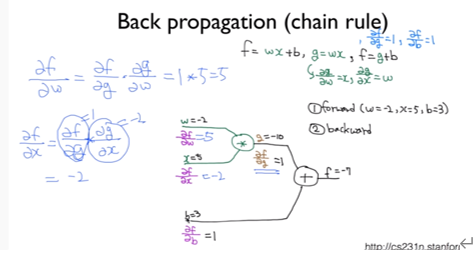
Back Propagation 연산에서 핵심은 'Chain Rule' 즉 연쇄법칙(함성함수의 도함수)입니다.
다시 말하지만 Back Propagation은 Cost를 최소화하기 위해 w를 갱신해야하며 이를 위해선 Cost의 미분값이 필요합니다. 이것이 위 이미지 좌측 상단의 '∂f / ∂w' 이고 이것을 구하는데 이용되는 것이 연쇄법칙인 것입니다.
'∂f / ∂w'을 [∂f//∂g와 ∂g/∂w의 곱] 으로 구할 수 있다는 부분에서 연쇄법칙이 이용됐음을 확인할 수 있습니다.
핵심은 우리가 하나의 Unit을 최적화하기 위해 Forward Propagation에선 엄청난 연산량이 필요했는데, Back Propagation에선 편미분값을 구해서 '한번의 곱셈'으로 아주 간단하게 구할 수 있다는 점입니다.
저런 방식으로 나머지 모든 Unit의 Cost 미분값을 간단하게 구하여 Neural Network를 최적화할 수 있습니다.
출처
https://box-world.tistory.com/19 <Box World : [머신러닝] Back Propagation(역전파) 정복하기>
