백준 2225번 합분해

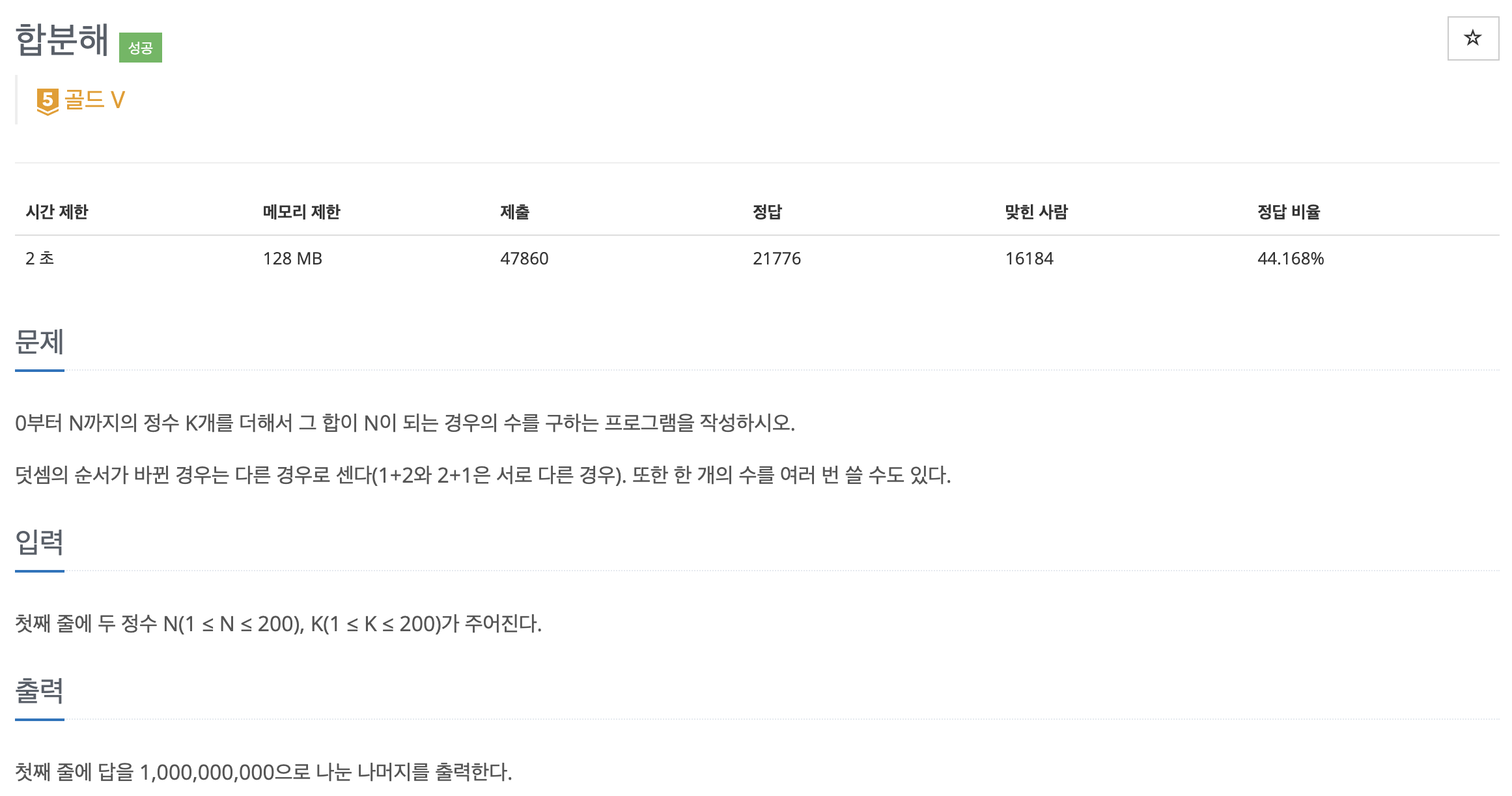
문제

백준 2225번 합분해 링크

풀이 방법

1. 패턴 파악하기

이 문제는 잘 보면 패턴을 파악할 수 있다. b개의 숫자를 더해서 a를 만드는 방식은 b-1개의 숫자로 c를 만들어 놓고 c와 마지막 숫자 d를 더하면 된다.
즉 마지막 숫자를 0 ~ a 중에서 하나로 잡고 b-1개의 숫자로 b-a를 만드는 방법들을 다 더해주면 된다.
전에 계산한 값들을 통해 다음 값을 계산할 수 있으므로 DP문제에 해당한다.

2. DP 배열 만들고 채우기

2차원 DP 배열을 만든다.

int [][] arr = new int[num+1][target+1]; // DP 배열 arr[i][j] -> i를 개를 더해서 j를 만들기

나는 위와 같이 선언해주었다. i는 몇개를 더할지를 의미하고 j는 더해서 몇을 만들지를 의미한다.

배열을 만든 뒤 배열을 채워주어야한다.

2-1. 1개로 만드는 경우를 1로 초기화

몇을 만들든 1개로 만드는 경우는 자기 자신을 더하는 경우밖에 없으므로 1로 초기화한다.

//1개로 만드는 경우
for(int i=0 ;i<=target; i++){
    arr[1][i] = 1; //1으로 초기화
}

2-2. 전의 계산한 값을 이용하도록 코드 작성

설명보다는 아래 코드를 보는 것이 도움이 될 것이다.
i는 몇개를 더할지를 의미하고 j는 무엇을 만들지를 의미한다. k는 마지막 수를 의미한다.
따라서 i는 1개부터 더할 수 있으므로 1부터 시작해서 주어진 최대 개수까지 반복하고, j는 0부터 target까지 만드는 경우를 모두 계산하기 위해 0부터 target까지 반복했다.
k는 마지막 수이므로 0부터 최대 현재 더할 수 있는 최대값인 j까지의 값을 가질 수 있으므로 0부터 j까지 반복했다.

// DP 적용
        for(int i=1; i<=num; i++){ // i개를 더해서
            for(int j=0; j<=target; j++){ // j를 만듦
                // arr[i][j] = arr[i-1]들 다 더하기
                for(int k = 0; k<=j; k++){
                    arr[i][j] = (arr[i][j] +  arr[i-1][j-k]) % 1_000_000_000;
                }
            }
        }

3. 답 출력하기

이제 DP 배열이 완성되었으므로 우리가 구하려는 값인 arr[num][target]을 출력해주면 된다. 이는 num개를 더해 target을 만드는 방법의 개수이다.

정답 코드

import java.io.*;
import java.util.StringTokenizer;

public class p2225 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw  = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st= new StringTokenizer(br.readLine());
        int target = Integer.parseInt(st.nextToken()); // 만들 수
        int num = Integer.parseInt(st.nextToken()); // 더할 개수
        int [][] arr = new int[num+1][target+1]; // DP 배열 arr[i][j] -> i를 개를 더해서 j를 만들기

        //1개로 만드는 경우
        for(int i=0 ;i<=target; i++){
            arr[1][i] = 1; //1으로 초기화
        }

        // DP 적용
        for(int i=1; i<=num; i++){ // i개를 더해서
            for(int j=0; j<=target; j++){ // j를 만듦
                // arr[i][j] = arr[i-1]들 다 더하기
                for(int k = 0; k<=j; k++){
                    arr[i][j] = (arr[i][j] +  arr[i-1][j-k]) % 1_000_000_000;
                }
            }
        }

        bw.write(arr[num][target]+"");
        bw.flush();
        bw.close();
    }
}