백준 다리만들기 2 17472

다리를 연결해서 모든 섬을 연결하는 문제

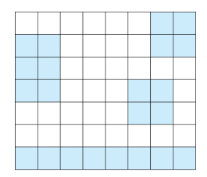
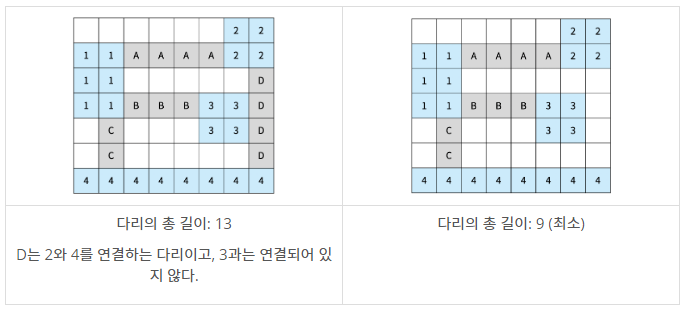
• 다리 길이가 최소가 되야함
• 한 다리의 길이는 최소 2

최소 스패닝 트리

노드 전부를 연결하는 최소 연결 트리

한마디로 노드가 n개이면 최소 스패닝 트리의 엣지는 n-1개이다

MST (Minimum Spanning Tree) 최소 신장 트리

각 간선의 가중치가 동일하지 않을 때 가중치 합이 최소인 최소 스패닝 트리

해결법

• 크루스칼 알고리즘
  사이클을 이루지 않는 가장 가중치가 작은 노드를 선택함
  선택 노드 수가 n-1일때까지 반복한다

• 프림 알고리즘
  정점을 기반으로 가중치가 작은 노드를 선택하면서 확장해나감

코드

초기화

for(int i=0;i<10;i++){
		for(int j=0;j<10;j++){
			iland[i][j]=999;
		}
	}

iland라는 맵을 999로 초기화

for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){
			if(map[i][j]==1){
				dfs(i,j);
				Cnt++;
			}
		}
	}

맵을 돌면서 섬마다 번호를 붙여준다

for(int i=0;i<10;i++){
		parent[i]=i;
	}

섬마다 이어졌는지 아닌지 확인할 수 있는 parent 배열을 자기자신으로 초기화해준다

풀이

for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){
			if(map[i][j]>0&&j+1<n&&map[i][j+1]==0){
				garo(map[i][j],i,j);
			}
			if(map[i][j]>0&&i+1<m&&map[i+1][j]==0){
				sero(map[i][j],i,j);
			}
		}
	}

for문으로 맵 전체를 돌면서
자기자신이 섬이면서(map[i][j]>0)
오른쪽 옆칸, 또는 아래칸이 존재하면서 바다인(map[i][j+1]==0 or map[i+1][j]==0)칸을 찾아나감
(다리를 놓을 가능성이 생긴다)
각각 조건이 맞다면 다리를 놓는 함수 실행

void garo(int ilandnum,int x,int y){
	int cnt=0;
	while(y+1<n){
		if(map[x][y+1]!=0){
			if(ilandnum<map[x][y+1]){
				if(cnt>1&&iland[ilandnum][map[x][y+1]]>cnt){
					iland[ilandnum][map[x][y+1]]=cnt;
				
				}
				
			}else{
				if(cnt>1&&iland[map[x][y+1]][ilandnum]>cnt){
					iland[map[x][y+1]][ilandnum]=cnt;
				
				}	
			}
				return;
		}
			y++;
			cnt++;
		
	}
}

가로로 다리를 놓는 함수
while문으로 맵의 오른쪽 끝에 도달할때까지 오른쪽으로 한칸씩 움직인다.
만약 또다른 섬에 닿았다면...
다리가 한칸보다 더 길다면(cnt>1) 저장해준다

for(int i=2;i<Cnt;i++){
		for(int j=i+1;j<Cnt;j++){
			if(iland[i][j]!=999){
				v.push_back(make_pair(iland[i][j],make_pair(i,j)));
			}
		}
	}
sort(v.begin(),v.end());

위에서 저장한 가능한 간선들을 벡터화해준다
그리고 가중치 크기에 따라 sort.

int sum=0;
	int c=0;
	for(int i=0;i<v.size();i++){
		int f1 = find(v[i].second.first);
		int f2 = find(v[i].second.second);
		if(f1!=f2){
			sum+=v[i].first;
			if(parent[f1]<parent[f2]){
				parent[f2]=f1;
			}else{
				parent[f1]=f2;
			}
			c++;
		}
		
	}
	if(c!=Cnt-3){
		printf("-1");
	}else{
		printf("%d",sum);
	}

벡터 내 간선들의 부모가 다르다면 (연결돼있지 않음)
parent를 같게 만들어준 다음 연결한다.

그리고 출력
끝!