Edge
한쪽 방향으로 픽셀 값이 급격히 바뀌는 부분
객체와 배경의 경계, 객체와 객체의 경계에서 발생
객체 판별을 위한 전처리로 사용
미분과 그래디언트
에지를 찾으려면 픽셀 값의 변화율 큰 픽셀 선택해야함
변화율 == 미분
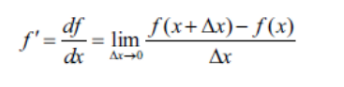
함수 값이
- 증가하면 양수
- 일정하면 0에 가까운 값
- 감소하면 음수
함수 그래프가 수평이면 미분값은 0
함수가 급격히 증가하면 미분값은 양수
함수가 감소하면 미분값은 음수
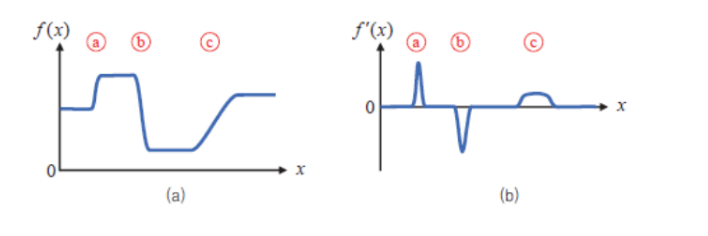
오른쪽의 그래프에서 값이 훨씬 크거나 작은 위치 찾아야함
영상의 미분
영상은
- 2차원 평면에서 정의된 함수임
- 정수 단위 좌표에 픽셀이 나열돼있음
1차원 이산함수에서는 일련의 데이터가 순서대로 나열돼 있을 시 미분 근사화 방법을 사용하여 변화량 측정함
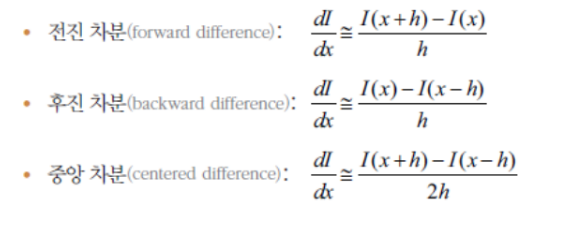
영상에 적용할 경우 h는 픽셀의 간격
(픽셀 간격의 최소 단위인 1을 h로 사용)
- 전진 차분 : I(x+1) - I(x) (자신 바로앞 픽셀 - 자기자신)
- 후진 차분 : I(x) - I(x-1)
- 중앙 차분 : (I(x+1) - I(x-1))/2 ( 자기 자신 제외하고 바로 앞과 뒤의 픽셀 이용)
이론적으로 중앙차분이 오류가 가장 적음
2차원 평면에서는 가로 세로 각각 미분해야함!
I(x,y)를 가로 방향으로 미분한다는 것은 y 좌표 고정한 상태에서 x축 방향으로만 미분근사 계산한다는 것 == 편미분
x축 편미분 Ix
y축 편미분 Iy
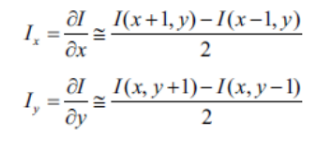
각각의 편미분을 중앙 차분 방법으로 근사화!
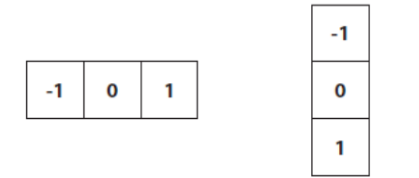
x축, y축 편미분하는 필터마스크
편미분 근사 수식을 쓰려면 마스크에 1/2 곱해야하는데 상대적 크기를 중요시하므로 단순화시킨 마스크 사용
에지 검출을 하면 변화가 큰 부분에서 값이 크거나 작은 픽셀이 나타남
그래디언트
2차원 공간의 x축, y축 방향 미분을 한꺼번에 벡터로 표현
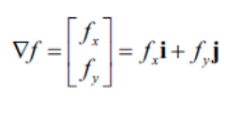
그래디언트는 벡터이기 때문에 크기와 방향 성분으로 표현 가능
- 방향은 변화가 큰 방향 나타냄
- 크기는 변화율의 세기 나타냄
크기는 보통 절대값으로 표기
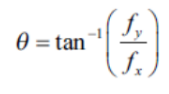
그래디언트 방향 수식
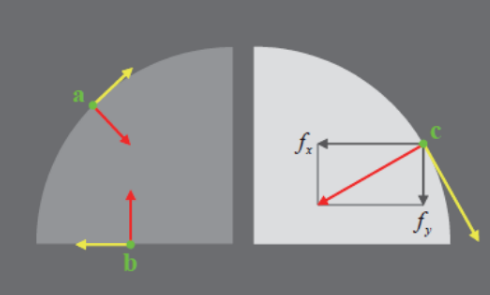
점 c에 대해서는 x축 편미분인 fx와 y축 편미분인 fy 성분 함께 표시
둘을 이용하여 빨간 화살표 도출 가능
노란 화살표는 그래디언트 벡터와 수직인 방향, 이를 에지의 방향이라 부름
그래디언트 기반 에지 검출
특정 값보다 그래디언트 크기가 크면 된다
기준을 threshold 라 부름
magnitude(x,y,outputArray)
x좌표와 y좌표를 이용하여 벡터의 크기 계산
x,y는 CV_32F 깊이를 사용하는 행렬 또는 벡터
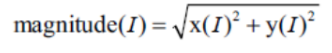
구성하는 원소 값은 이 수식으로 계산됨
phase(x,y,angle, bool angleInDegrees)
그래디언트 방향을 계산하고 싶으면 사용
x,y는 입력, angle은 방향을 나타내는 출력 행렬
a
마스크 기반 에지 검출
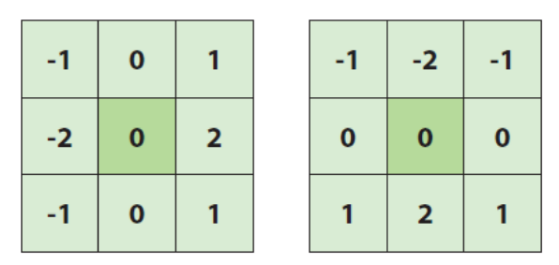
각각 x,y축 방향으로 편미분을 구하는 소벨마스크
현재 행에 대한 중앙 차분 연산을 2회, 이전, 다음행 중앙차분 1회 수행
소벨 필터
Sobel() 함수로 3*3 소벨 마스크 또는 확장된 형태의 마스크 이용
Sobel(src, dst, int ddepth, dx,dy, ksize, scale, delta,borderType)
입력, 출력, 출력 영상의 깊이, xy방향 미분차수, 소벨 커널 크기, 필터링 연산후 추가적으로 곱할 값, 더할 값, 가장자리 확장 방식)
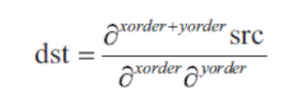
샤르 필터
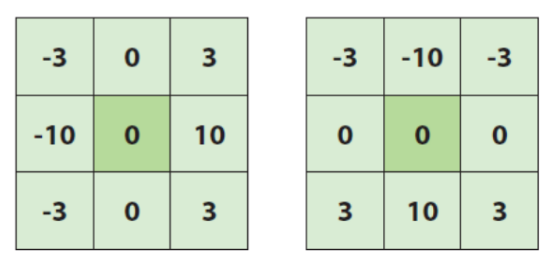
3*3 소벨 필터보다 더 정확한 미분 계산하는 것으로 알려짐
캐니 에지 검출기
에지 검출을 최적화
그래디언트의 크기와 방향 모두 고려하여 더 정확한 에지 위치 찾을 수 있음
과정
- 가우시안 필터링
잡음 제거한다 - 그래디언트 계산
3*3 소벨 마스크 사용
그래디언트 크기
- L1 norm : |변화율 f| = |fx| + |fy|
연산속도 향상 - L2 norm : |변화율 f| = (|fx|^2 + |fy|^2)^1/2
기본적으로 L1 norm 사용
-
비최대 억제
에지 근방의 여러 픽셀이 한꺼번에 에지로 검출됨
에지가 두껍게 표현되는 것을 방지
local maximum인 픽셀만 에지로 설정
주변을 둘러싼 모든 픽셀 검사하여 국지적 최대인지 판별,
그래디언트 벡터의 방향과 같은 방향의 픽셀만 검사 수행 -
이중 임계값 이용한 히스테리시스 에지 트래킹
하나의 임계값 사용시 환경 변화에 민감
T high, T low로 나눔
두 임계값 사이면 추가적 검사 진행
strong edge > T high >weak edge > T low
마지막에 히스테리시스 에지 트래킹 방식 사용해서 최종적으로 에지로 판별할 픽셀 선택
히스테리시스 에지 트래킹
약한 에지가 강한 에지 픽셀과 연결되어 있다면 최종적 에지로 판단
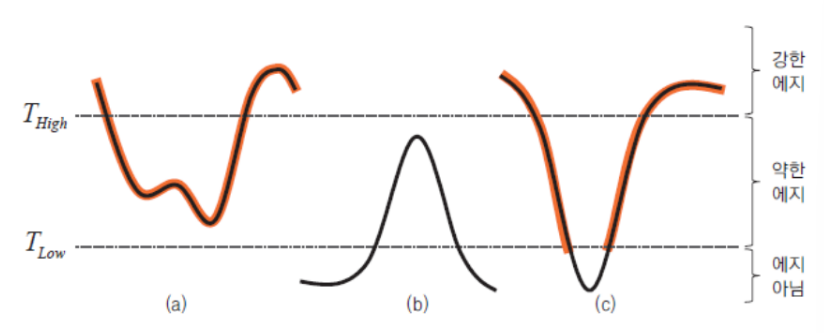
Canny() 함수에 구현
직선, 원 검출
허프 변환 직선 검출
2차원 xy 좌표에서 직선의 방정식을 파라미터 공간으로 변환
y = ax +b
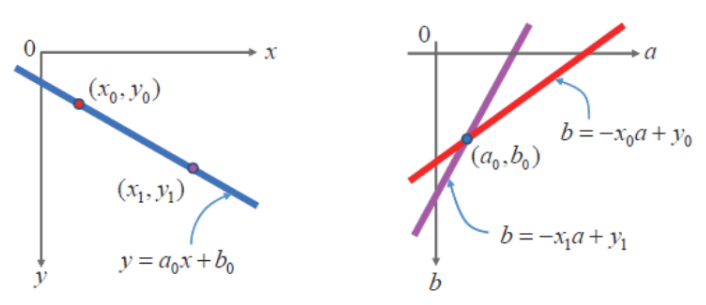
xy 좌표공간에서 ab 파라미터 공간으로 허프 변환
모든 에지 판별 점에 대하여 ab 파라미터 공간 직선으로 변환
직선이 많이 교차되는 점을 찾아야 함
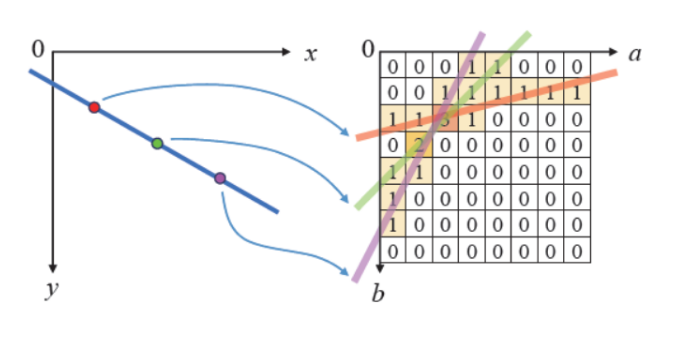
축적 배열에서 최대값을 찾아서 a,b 검출, 직선 뽑아냄
실제로는 극좌표계 사용
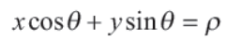
직선 좌표계는 y축 평행 직선 검출이 안되기 때문
- p : 원점에서 직선까지 수직거리
- 델타 : 원점에서 직선에 수직선 내렸을 때 x축과 이루는 각도
이 경우 x,y 공간에서 한 점은 공간에서 삼각함수 그래프 형태의 곡선으로 표현됨
공간에서 한 점은 xy 공간에서 직선
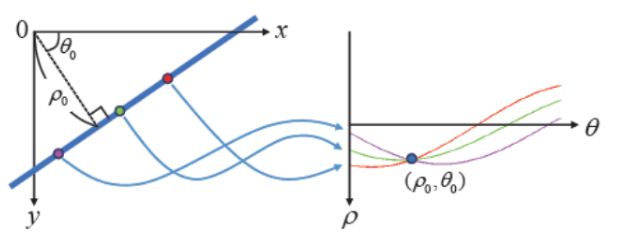
houge_lines() 함수에서는 Canny 함수로 에지 영상 구하고 이것을 HoughLines() 함수 입력으로 사용하여 직선 검출
허프 변환 원 검출
축적 배열을 사용하려면 많은 메모리, 연산시간 필요
일반적 허프 변환 대신 허프 그래디언트 방법을 이용
영상에 존재하는 모든 원의 중심 좌표를 찾고
검출된 원의 중심으로부터 원에 적합한 반지름 찾음
중심 찾는 과정에서 축적 배열 사용
축적 배열은 입력 영상과 동일한 xy 좌표공간에서 2차원 배열로 만듦
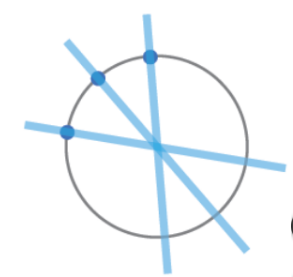
그래디언트 방향 직선상 축적 배열 증가시키면 결과적으로 원의 중심 위치에 축적 배열 값이 크게 나타남
