정렬(sorting)

• 항목값의 대소 관계에 따라 데이터 집합을 일정한 순서로 바꾸어 늘어놓는 작업
• 정렬 알고리즘의 핵심은 교환/선택/삽입

정렬 알고리즘의 안정성

• 정렬 알고리즘은 안정적인(stable) 알고리즘과 그렇지 않은 알고리즘으로 나타낼 수 있음
  

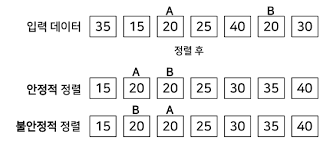
안정적인 알고리즘

• 정렬한 후에도 값이 같은 원소의 순서가 유지되는 것

안정적이지 않은 알고리즘

• 정렬 후 원래의 순서가 유지된다는 보장을 할 수 없는 것

내부 정렬과 외부 정렬

내부 정렬

• 정렬할 모든 데이터를 하나의 배열에 저장할 수 있는 경우

외부 정렬

• 정렬할 데이터가 많아서 하나의 배열에 저장할 수 없는 경우
• 내부 정렬을 응용한 것으로, 구현하려면 별도로 작업용 파일이 필요함

버블 정렬(bubble sort)

• 두 원소의 대소 관계를 비교하여 필요에 따라 교환을 반복(단순 교환 정렬)

버블 정렬의 원리

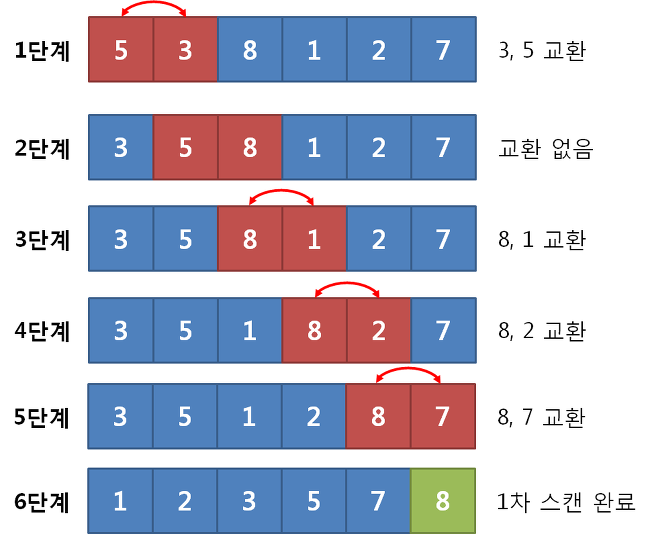
1. 이웃한 원소를 비교하고, 필요하면 교환.
2. 원소 수가 n인 배열에서 n - 1번 비교/교환을 하게 됨
3. 이러한 일련의 과정을 패스라고 함(총 n-1번의 패스를 수행해야 함)
4. 첫 번째 패스가 끝나면 n-2번 비교/교환을 함(두번 째 패스)
5. 반복

버블 정렬 프로그램

from typing import MutableSequence

def bubble_sort(a: MutableSequence) -> None:
    """버블 정렬"""
    n = len(a)
    for i in range(n - 1):
        for j in range(n - 1, i, -1):
            if a[j - 1] > a[j]:
                a[j - 1], a[j] = a[j], a[j - 1]

• 원소를 비교하는 횟수
  (n - 1) + (n - 2) + ... + 1 = n(n-1) / 2
• 실제 교환하는 횟수는 원솟값에 영향을 받음으로 위 도출결과의 절반인 n(n-1) / 4임

알고리즘 개선 1

• x 번째 패스에서 교환이 한 번도 이루어지지 않았으면 해당 배열은 이미 정렬된 것임

def bubble_sort(a: MutableSequence) -> None:
    """버블 정렬(교환 횟수에 따른 중단)"""
    n = len(a)
    for i in range(n - 1):
        exchng = 0  # 패스에서 교환 횟수
        for j in range(n - 1, i, -1):
            if a[j - 1] > a[j]:
                a[j - 1], a[j] = a[j], a[j - 1]
                exchng += 1
        if exchng == 0:
            break

알고리즘 개선 2

• 각각의 패스에서 비교/교환을 하다가 특정 원소 이후에 교환하지 않으면 그 원소보다 앞쪽에 있는 원소는 이미 정렬을 마친 것임

def bubble_sort(a: MutableSequence) -> None:
    """버블 정렬(스캔 범위를 제한)"""
    n = len(a)
    k = 0
    while k < n - 1:
        last = n - 1
        for j in range(n - 1, k, -1):
            if a[j - 1] > a[j]:
                a[j - 1], a[j] = a[j], a[j - 1]
                last = j
        k = last

셰이커 정렬

• 버블 정렬을 개선한 알고리즘으로, 양방향 버블정렬, 칵테일 정렬이라고도 함
• 홀수 패스에서는 가장 작은 원소를 맨 앞으로 이동시키고, 짝수 패스에서는 가장 큰 원소를 맨 뒤로 이동시켜 패스의 스캔 방향을 번갈아 바꾸는 것

def shaker_sort(a: MutableSequence) -> None:
    """셰이커 정렬"""
    left = 0
    right = len(a) - 1
    last = right
    while left < right:
        for j in range(right, left, -1):
            if a[j - 1] > a[j]:
                a[j - 1], a[j] = a[j], a[j - 1]
                last = j
        left = last

        for j in range(left, right):
            if a[j] > a[j + 1]:
                a[j], a[j + 1] = a[j + 1], a[j]
                last = j
        right = last

단순 선택 정렬

• 가장 작은 원소부터 선택해 알맞은 위치로 옮기는 것

  1. 아직 정렬하지 않은 부분에서 값이 가장 작은 원소를 선택
  2. 아직 정렬하지 않은 부분에서 맨 앞에 있는 원소를 교환

def selection_sort(a: MutableSequence) -> None:
    """단순 선택 정렬"""
    n = len(a)
    for i in range(n - 1):
        min = i  # 정렬 할 부분에서 가장 작은 원소의 인덱스
        for j in range(i + 1, n):
            if a[j] < a[min]:
                min = j
        a[i], a[min] = a[min], a[i]  # 정렬 할 부분에서 맨 앞의 원소와 가장 작은 원소를 교환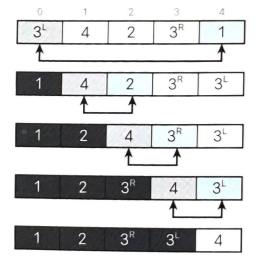 

• 단순 선택 정렬 알고리즘의 비교횟수는 (n^2-n) / 2번임
• 위 그림에서 알 수 있듯이 안정적이지 않은 정렬임

단순 삽입 정렬

• 주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘
• 단순 선택 정렬과 비슷하지만 값이 가장 작은 원소를 선택하지 않음

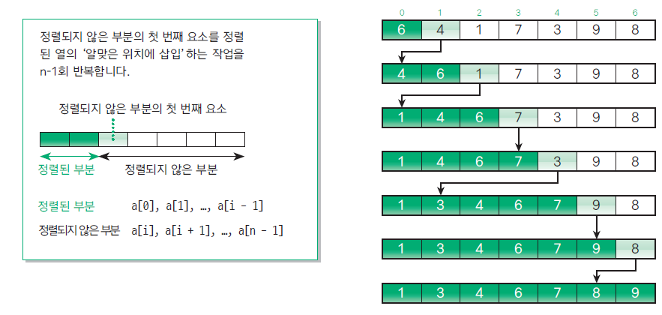
1. 두번째 원소를 첫번째 원소와 비교 후 정렬
2. 세번째 원소를 앞쪽 정렬 완료된 부분과 비교해 알맞은 위치에 삽입
3. 반복

def insertion_sort(a: MutableSequence) -> None:
    """단순 삽입 정렬"""
    n = len(a)
    for i in range(1, n):
        j = i
        tmp = a[i]
        while j > 0 and a[j - 1] > tmp:
            a[j] = a[j - 1]
            j -= 1
        a[j] = tmp

• 서로 떨어져 있는 원소를 교환하지 않으므로 안정적임
• 비교횟수와 교환횟수는 모두 n^2 / 2번임

셸 정렬

• 단순 삽입 정렬의 장점(정렬이 거의 돼있는 상태에서는 속도가 아주 빠름)은 살리고 단점(삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아짐)은 보완한 알고리즘
• 정렬할 배열의 원소를 그룹으로 나눠 각 그룹별로 정렬을 수행
  

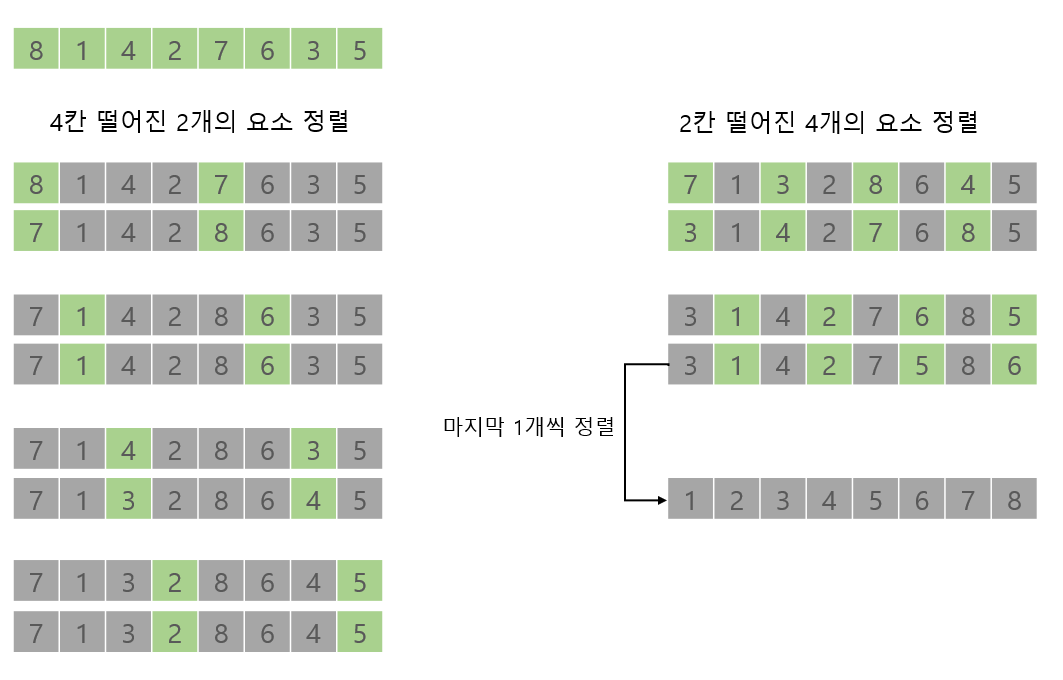
셸 정렬 프로그램

def shell_sort(a: MutableSequence) -> None:
    """셸 정렬"""
    n = len(a)
    h = n // 2
    while h > 0:
        for i in range(h, n):
            j = i - h
            tmp = a[i]
            while j >= 0 and a[j] > tmp:
                a[j + h] = a[j]
                j -= h
            a[j + h] = tmp
        h //= 2

• 이웃하지 않고 떨어져있는 원소를 서로 교환하므로 안정적이지 않음

퀵 정렬

• 가장 빠른 정렬 알고리즘으로 널리 사용됨
  

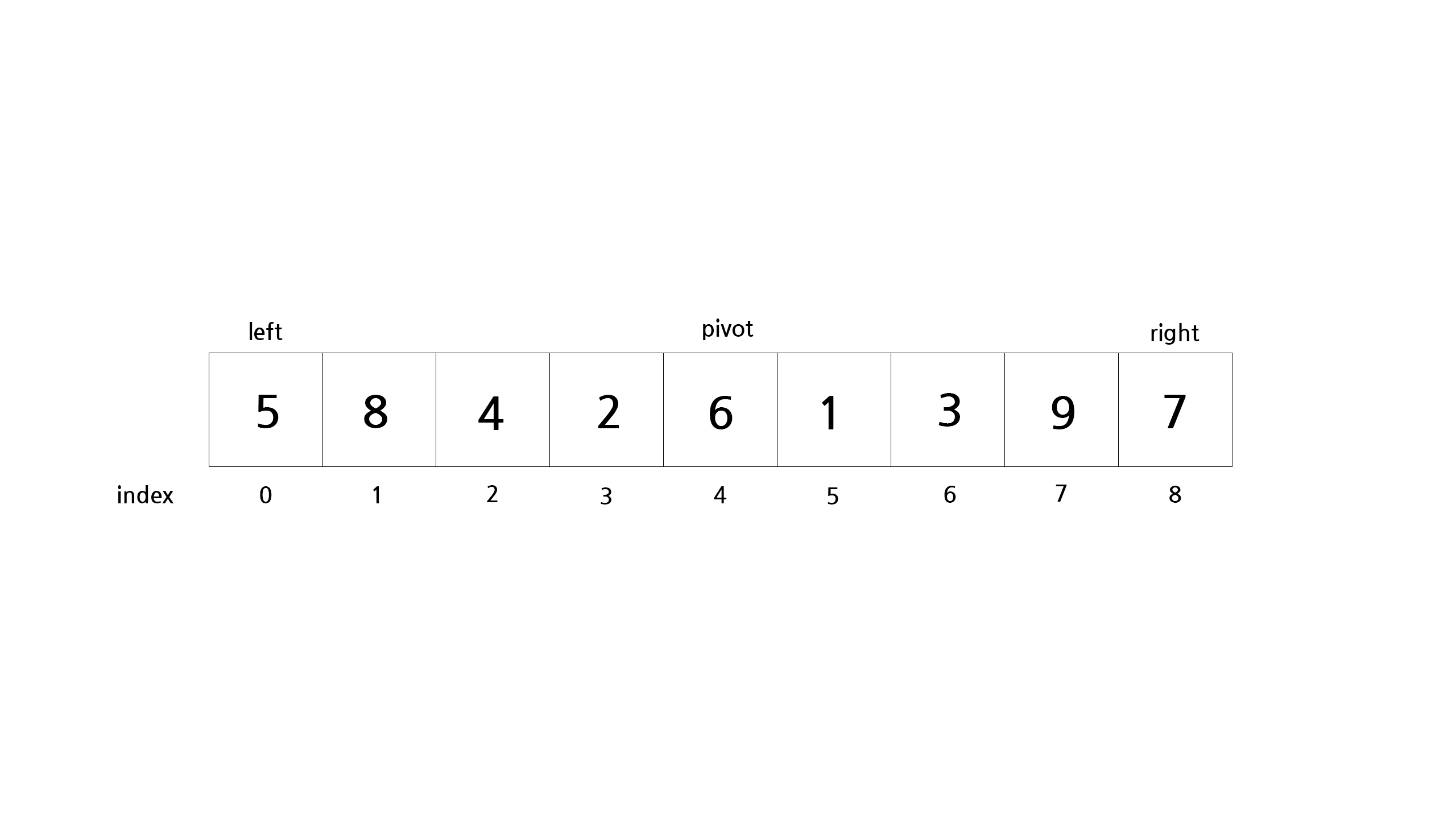
  가운데를 피벗(x)으로 놓고, 왼쪽 끝 원소를 pl, 오른쪽 끝 원소를 pr으로 둠

• a[pl] >= x가 성립하는 원소를 찾을 때 까지 pl을 오른쪽 방향으로 스캔
• a[pr] <= x가 성립하는 원소를 찾을 때 까지 pr을 왼쪽 방향으로 스캔
• 양 쪽 다 해당 원소를 찾으면 두 원소를 바꿈
• 반복
• pl과 pr이 교차하면 피벗을 기준으로 피벗 이하인 그룹, 피벗 이상인 그룹으로 나뉨

배열을 두 그룹으로 나누기

def partition(a: MutableSequence) -> None:
    """배열을 분할하여 출력"""
    n = len(a)
    pl = 0         # 왼쪽 커서
    pr = n - 1     # 오른쪽 커서
    x = a[n // 2]  # 피벗(가운데 원소)

    while pl <= pr:
        while a[pl] < x: pl += 1
        while a[pr] > x: pr -= 1
        if pl <= pr:
            a[pl], a[pr] = a[pr], a[pl]
            pl += 1
            pr -= 1

퀵 정렬 만들기

• 위 코드를 재귀호출하면 퀵 정렬 알고리즘이 됨
  def qsort(a: MutableSequence, left: int, right: int) -> None:

    """a[left] ~ a[right]를 퀵 정렬"""
    pl = left                   # 왼쪽 커서
    pr = right                  # 오른쪽 커서
    x = a[(left + right) // 2]  # 피벗(가운데 요소)

    while pl <= pr:    # 실습 6-10과 같은 while 문
        while a[pl] < x: pl += 1
        while a[pr] > x: pr -= 1
        if pl <= pr:
            a[pl], a[pr] = a[pr], a[pl]
            pl += 1
            pr -= 1

    if left < pr: qsort(a, left, pr)
    if pl < right: qsort(a, pl, right)

def quick_sort(a: MutableSequence) -> None:
    """퀵 정렬"""
    qsort(a, 0, len(a) - 1)

병합 정렬

• 배열을 앞부분과 뒷부분 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘

정렬을 마친 배열의 병합