트리 구조

• 데이터 사이의 계층 관계를 표현
  

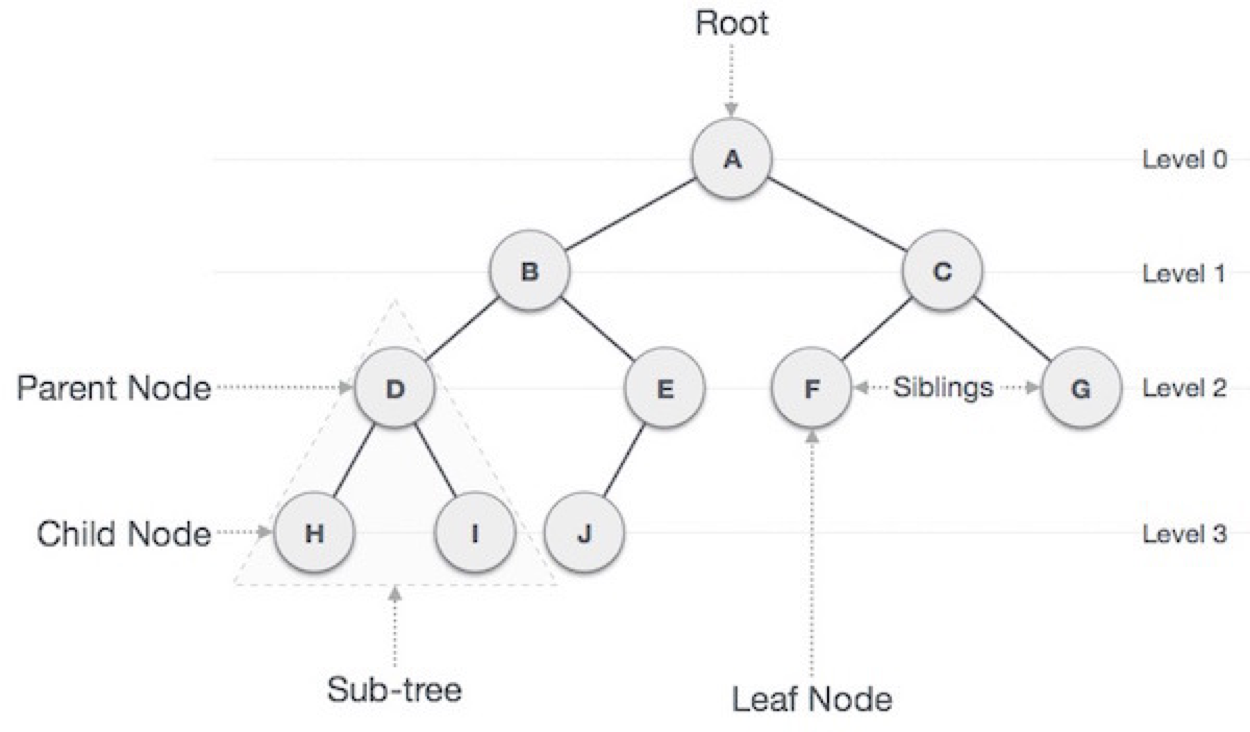
트리 구조 관련용어

• 루트
  가장 위쪽에 있는 노드
• 리프
  가장 아래쪽에 있는 노드(단말 노드), 물리적으로 가장 밑이 아닌, 더 이상 뻗어나갈 수 없는 마지막 노드
• 비단말 노드
  리프를 제외한 노드
• 자식
  어떤 노드와 가지가 연결됐을 때 아래쪽 노드
• 부모
  어떤 노드와 가지가 연결됐을 때 위쪽에 있는 노드
• 형제
  부모가 같은 노드
• 조상
  어떤 노드에서 위쪽으로 가지를 따라가면 만나는 모든 노드
• 자손
  어떤 노드에서 아래쪽으로 가지를 따라가면 만나는 모든 노드
• 레벨
  루트에서 얼마나 멀리 떨어져 있는 지 나타내는 것
• 차수
  각 노드가 갖는 자식의 수
• 높이
  루트에서 가장 멀리 있는 리프까지 거리(리프 레벨의 최댓값)
• 서브트리
  어떤 노드를 루트로 하고, 그 자손으로 구성된 트리
• 빈 트리
  노드와 가지가 전혀 없는 트리

순서 트리와 무순서 트리

• 형제 노드의 순서관계가 있는지에 따라 구분, 순서 관계가 있으면 순서 트리, 구별하지 않으면 무순서 트리라고 함

순서 트리의 검색

너비 우선 검색(BFS)

• 폭 우선 검색, 가로 검색, 수평 검색
• 낮은 레벨부터 왼쪽에서 오른쪽으로 검색을 마치고 다음 레벨로 넘어가는 방법
  

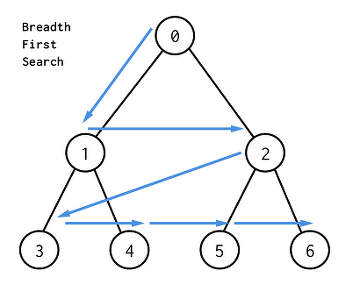
0 > 1 > 2 > 3 > 4 > 5 > 6

깊이 우선 검색(DFS)

• 세로 검색, 수직 검색
• 리프에 도달할 때까지 아래쪽으로 내려가면서 검색
• 리프에 도달해서 더 이상 검색할 곳이 없으면 부모 노드로 돌아간 뒤 다시 자식 노드로 내려감

전위 순회

• 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
  

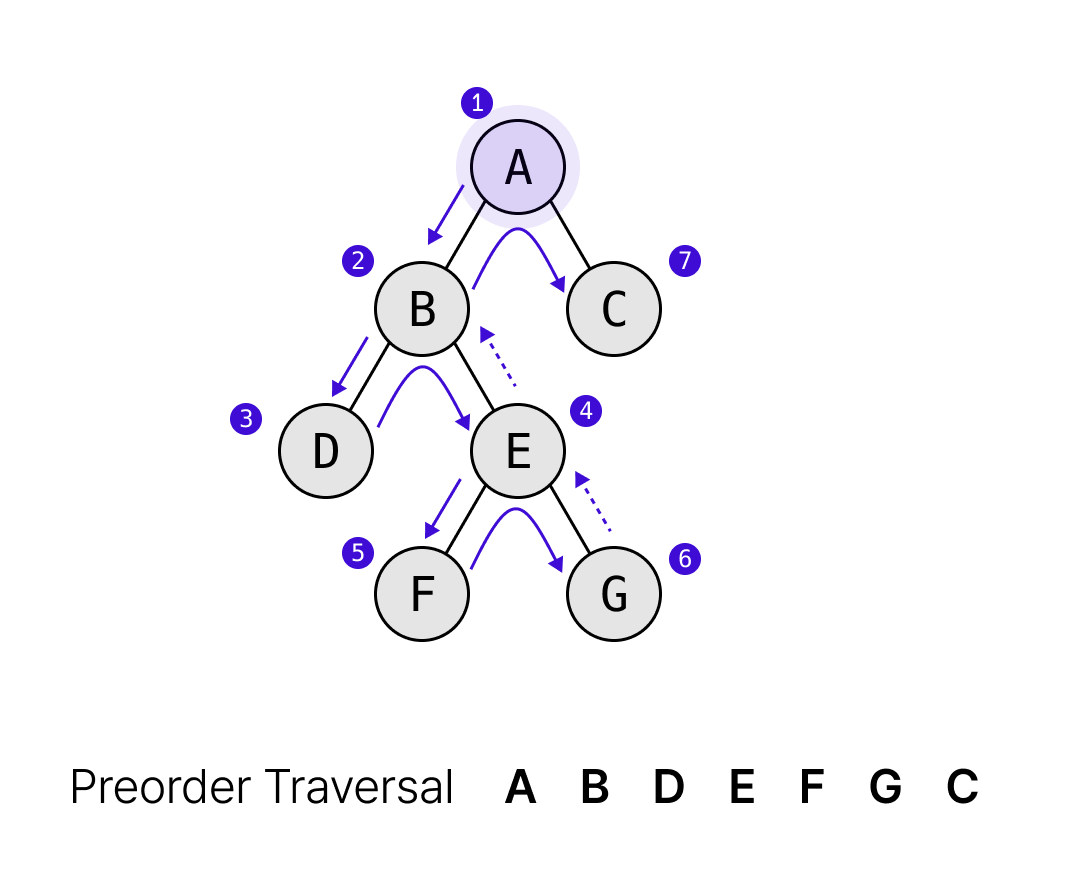
중위 순회

• 왼쪽자식 -> 노드 방문 -> 오른쪽 자식
  

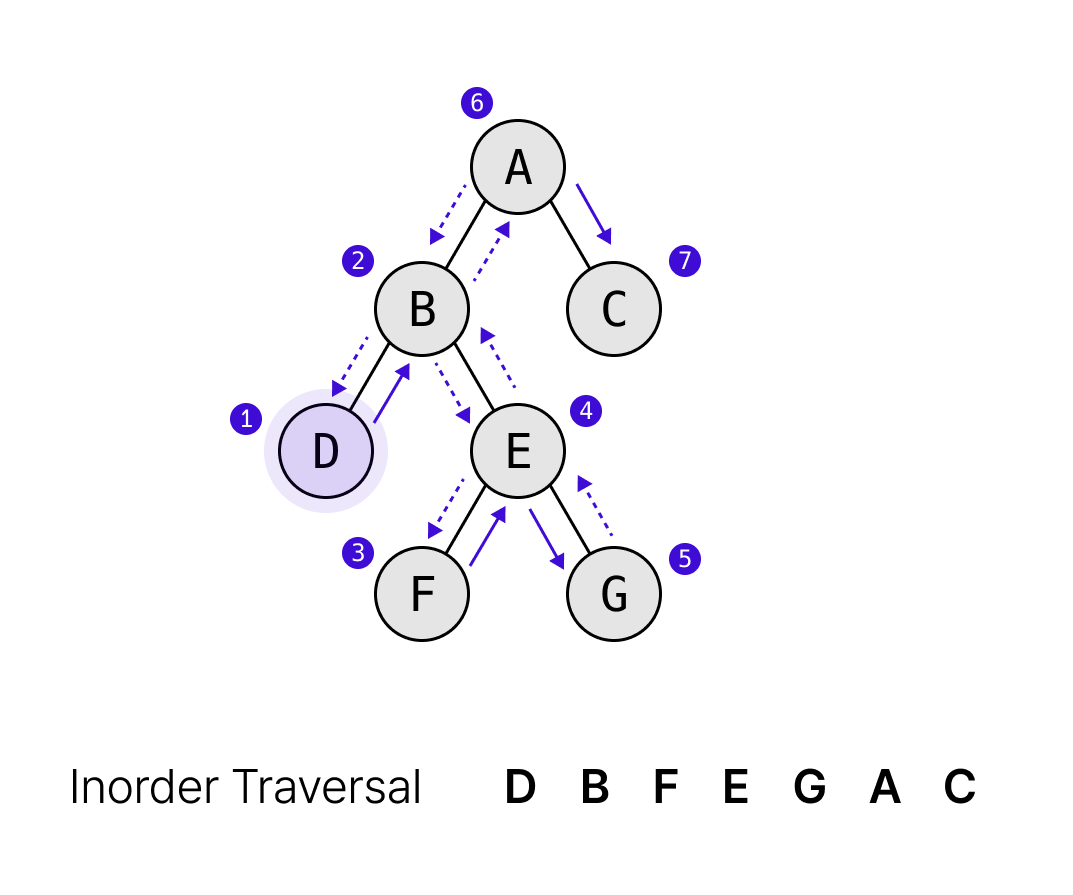
후위 순회

• 왼쪽 자식 -> 오른쪽 자식 -> 노드 방문
  

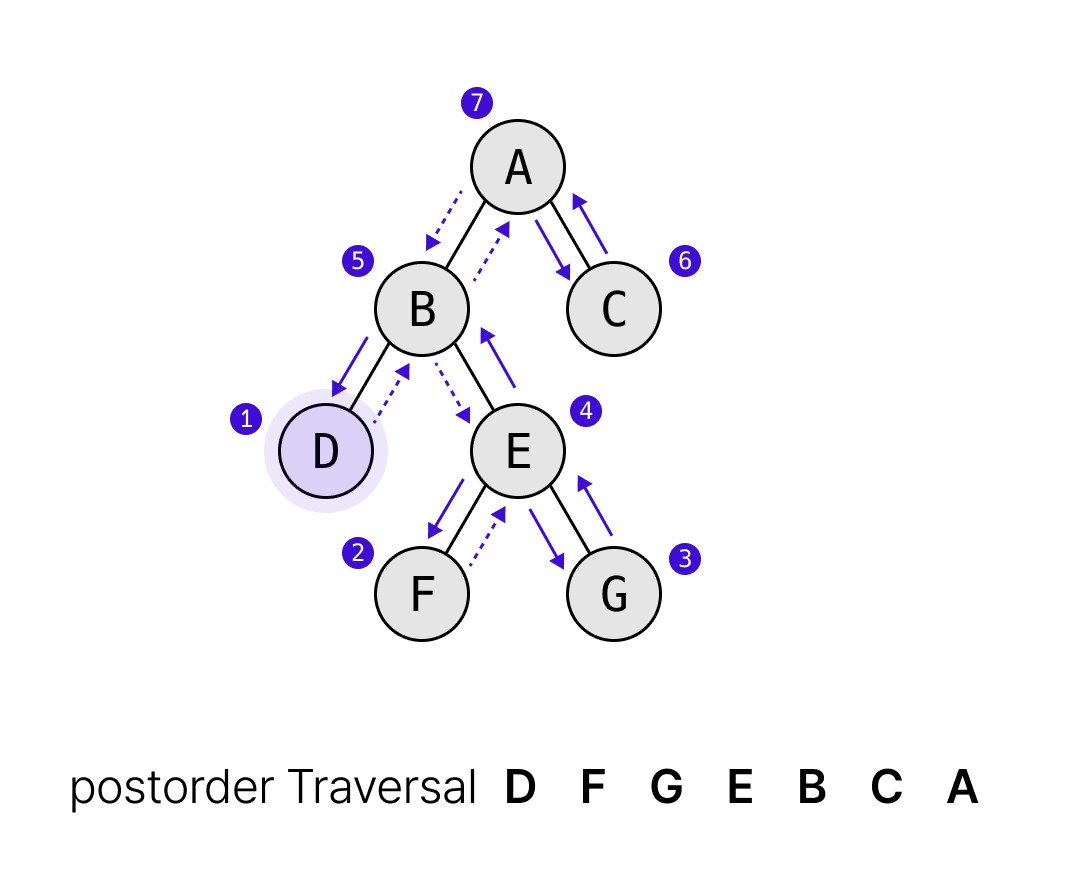
이진 트리와 이진 검색 트리

이진 트리

• 노드가 왼쪽 자식, 오른쪽 자식 2개 만을 갖는 트리
• 이 때 두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관 없음.
• 왼쪽과 오른쪽 자식을 구분한다는 특징이 있음.
  -> 왼쪽 서브트리, 오른쪽 서브트리로 구분 가능

완전 이진 트리

• 루트부터 아래쪽 레벨로 노드가 가득 차 있고, 같은 레벨 안에서 왼쪽부터 오른쪽으로 노드가 채워져있는 이진 트리
  

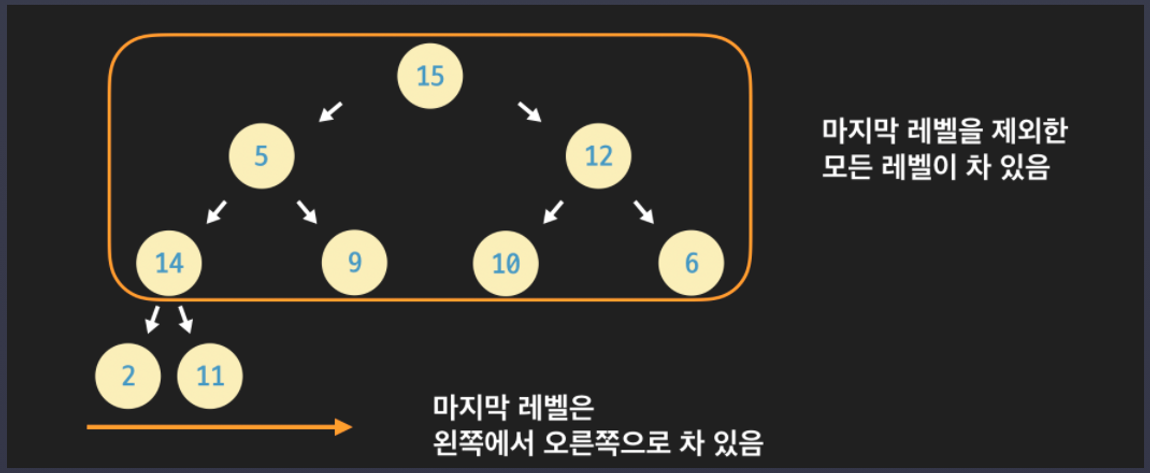
  마지막 레벨을 제외하고 모든 레벨에 노드가 가득 차있음
  마지막 레벨에 한해서 왼쪽부터 오른쪽으로 노드를 채우되, 끝까지 채우지 않아도 괜찮음

이진 검색 트리

• 왼쪽 서브트리 노드의 키값은 자신의 노드 키값보다 작아야 함
• 오른쪽 서브트리 노드의 키값은 자신의 노드 키값보다 커야함

  이진 검색 트리를 중위 순회의 DFS로 스캔하면 오름차순으로 정렬 가능

이진 검색 트리 프로그램

from __future__ import annotations
from typing import Any, Type

class Node:
    """이진 검색 트리의 노드"""
    def __init__(self, key: Any, value: Any, left: Node = None,
                 right: Node = None):
        """생성자"""
        self.key = key      # 키
        self.value = value  # 값
        self.left = left    # 왼쪽 포인터(왼쪽 자식 참조)
        self.right = right  # 오른쪽 포인터(오른쪽 자식 참조)

class BinarySearchTree:
    """이진 검색 트리"""

    def __init__(self):
        """초기화"""
        self.root = None  # 루트

# Do it! 실습 9-1[B]
    def search(self, key: Any) -> Any:
        """키 key를 갖는 노드를 검색"""
        p = self.root           # 루트에 주목
        while True:
            if p is None:       # 더 이상 진행할 수 없으면
                return None     # 검색 실패
            if key == p.key:    # key와 노드 p의 키가 같으면
                return p.value  # 검색 성공
            elif key < p.key:   # key 쪽이 작으면
                p = p.left      # 왼쪽 서브 트리에서 검색
            else:               # key 쪽이 크면
                p = p.right     # 오른쪽 서브 트리에서 검색

# Do it! 실습 9-1[C]
    def add(self, key: Any, value: Any) -> bool:
        """키가 key이고, 값이 value인 노드를 삽입"""

        def add_node(node: Node, key: Any, value: Any) -> None:
            """node를 루트로 하는 서브 트리에 키가 key이고, 값이 value인 노드를 삽입"""
            if key == node.key:
                return False  # key가 이진검색트리에 이미 존재
            elif key < node.key:
                if node.left is None:
                    node.left = Node(key, value, None, None)
                else:
                    add_node(node.left, key, value)
            else:
                if node.right is None:
                    node.right = Node(key, value, None, None)
                else:
                    add_node(node.right, key, value)
            return True

        if self.root is None:
            self.root = Node(key, value, None, None)
            return True
        else:
            return add_node(self.root, key, value)

# # Do it! 실습 9-1[D]
    def remove(self, key: Any) -> bool:
        """키가 key인 노드를 삭제"""
        p = self.root           # 스캔 중인 노드
        parent = None           # 스캔 중인 노드의 부모 노드
        is_left_child = True    # p는 parent의 왼쪽 자식 노드인지 확인

        while True:
            if p is None:       # 더 이상 진행할 수 없으면
                return False    # 그 키는 존재하지 않음

            if key == p.key:    # key와 노드 p의 키가 같으면
                break           # 검색 성공
            else:
                parent = p                  # 가지를 내려가기 전에 부모를 설정
                if key < p.key:             # key 쪽이 작으면
                    is_left_child = True    # 여기서 내려가는 것은 왼쪽 자식
                    p = p.left              # 왼쪽 서브 트리에서 검색
                else:                       # key 쪽이 크면
                    is_left_child = False   # 여기서 내려가는 것은 오른쪽 자식
                    p = p.right             # 오른쪽 서브 트리에서 검색

        if p.left is None:                  # p에 왼쪽 자식이 없으면
            if p is self.root:
                self.root = p.right
            elif is_left_child:
                parent.left = p.right       # 부모의 왼쪽 포인터가 오른쪽 자식을 가리킴
            else:
                parent.right = p.right      # 부모의 오른쪽 포인터가 오른쪽 자식을 가리킴
        elif p.right is None:               # p에 오른쪽 자식이 없으면
            if p is self.root:
                self.root = p.left
            elif is_left_child:
                parent.left = p.left        # 부모의 왼쪽 포인터가 왼쪽 자식을 가리킴
            else:
                parent.right = p.left       # 부모의 오른쪽 포인터가 왼쪽 자식을 가리킴
        else:
            parent = p
            left = p.left                   # 서브 트리 안에서 가장 큰 노드
            is_left_child = True
            while left.right is not None:   # 가장 큰 노드 left를 검색
                parent = left
                left = left.right
                is_left_child = False

            p.key = left.key                # left의 키를 p로 이동
            p.value = left.value            # left의 데이터를 p로 이동
            if is_left_child:
                parent.left = left.left     # left를 삭제
            else:
                parent.right = left.left    # left를 삭제
        return True

# Do it! 실습 9-1[E]
    def dump(self) -> None:
        """덤프(모든 노드를 키의 오름차순으로 출력)"""

        def print_subtree(node: Node):
            """node를 루트로 하는 서브 트리의 노드를 키의 오름차순으로 출력"""
            if node is not None:
                print_subtree(node.left)            # 왼쪽 서브 트리를 오름차순으로 출력
                print(f'{node.key}  {node.value}')  # node를 출력
                print_subtree(node.right)           # 오른쪽 서브 트리를 오름차순으로 출력

        print_subtree(self.root)

# Do it! 실습 9-1[F]
    def min_key(self) -> Any:
        """가장 작은 키"""
        if self.root is None:
            return None
        p = self.root
        while p.left is not None:
            p = p.left
        return p.key

    def max_key(self) -> Any:
        """가장 큰 키"""
        if self.root is None:
            return None
        p = self.root
        while p.right is not None:
            p = p.right
        return p.key