KATA#73

WHAT IS KATA?

KATA는 기술과 기술 향상에 초점을 맞춘 코드 챌린지입니다.
일부는 프로그래밍 기본 사항을 교육하는 반면 다른 일부는 복잡한 문제 해결에 중점을 둡니다.

이 용어는 The Pragmatic Programmer 라는 책의 공동 저자인 Dave Thomas 가
무술에서 일본의 카타 개념을 인정하면서 처음 만들어졌습니다.
Dave의 개념 버전은 코드 카타를 프로그래머가
연습과 반복을 통해 기술을 연마하는 데 도움이 되는 프로그래밍 연습으로 정의합니다.

---

- SQL

---

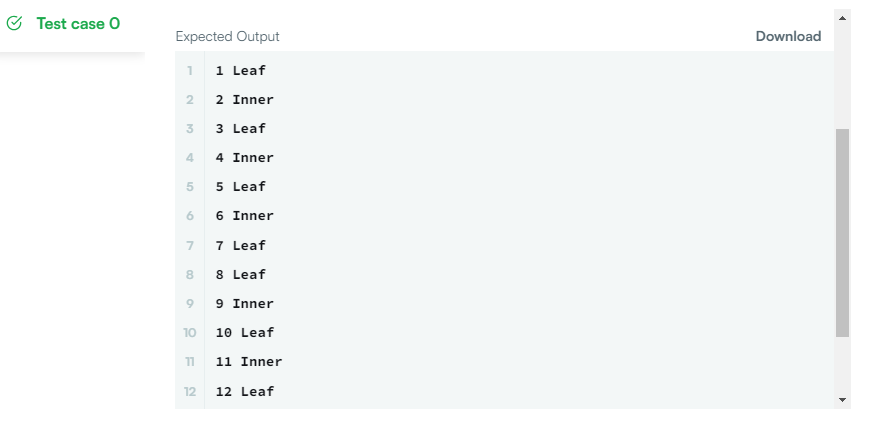
✔️ 문제 #1: Binary Tree Nodes

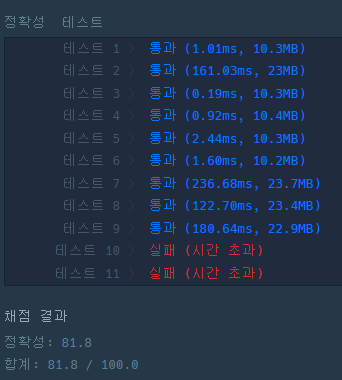
✔️ 제출 쿼리

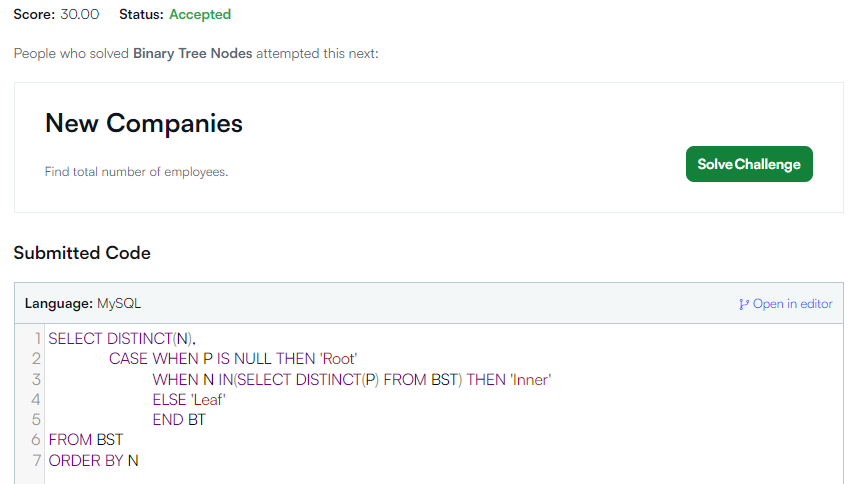
✔️ 쿼리 분석

SELECT DISTINCT(N),
       CASE WHEN P IS NULL THEN 'Root'
            WHEN N IN(SELECT DISTINCT(P) FROM BST) THEN 'Inner'
            ELSE 'Leaf' 
            END BT
FROM BST
ORDER BY N

---

- PYTHON

---

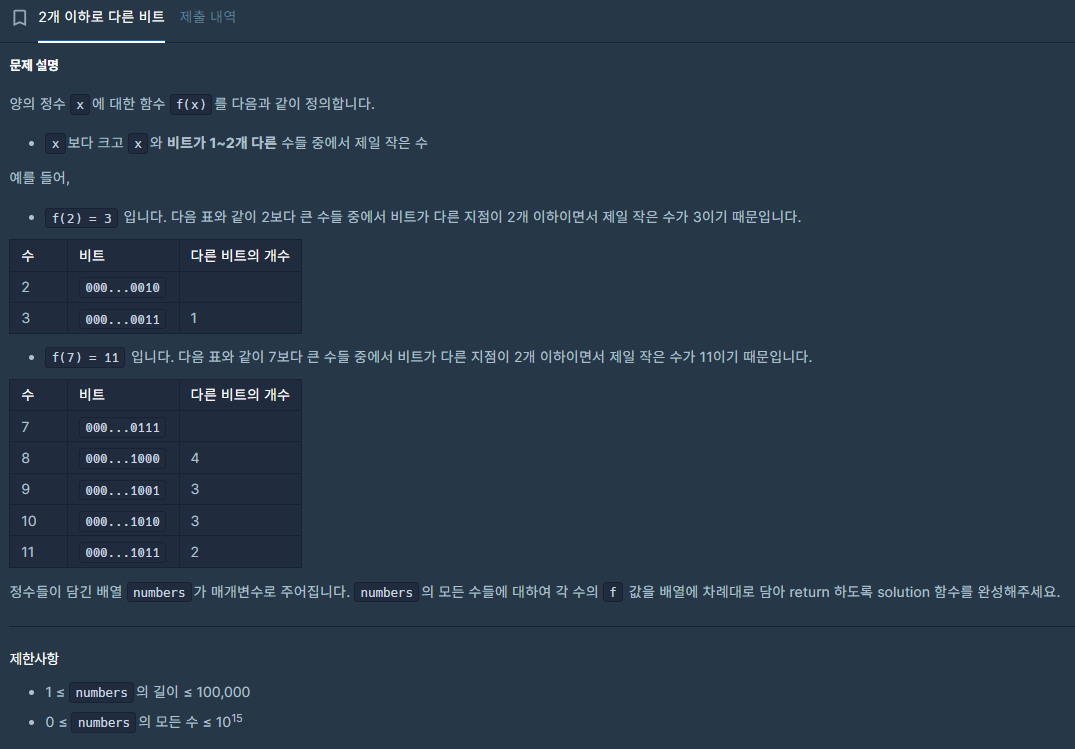
✔️ 문제 #1: 2개 이하로 다른 비트

✔️ 제출 코드

✔️ 코드 분석

1. 비트 차이 개수를 계산하는 함수를 생성하고,
   X 보다 큰 숫자를 하나씩 비교하면서 비트 차이가 2개 이하일 때 그 숫자를 반환하는 함수로
   코드를 제출했는데, 테스트 케이스 중 시간 초과로 통과되지 않았다.

# 두 숫자 a와 b 사이의 비트 차이 개수를 계산하는 함수 생성
def count_diff_bits(a, b):
    # XOR 연산을 통해 두 숫자의 비트가 다른 위치 찾기
    xor_result = a ^ b
    # XOR 결과를 이진수 문자열로 변환
    binary_representation = bin(xor_result)
    # 이진수 문자열에서 '1'의 개수를 셈
    diff_bits = binary_representation.count('1')
    # 두 숫자 간의 비트 차이 개수를 반환
    return diff_bits

# x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수를 찾는 함수 생성
def find_f(x):
    # x보다 큰 수를 찾기 위해 초기 후보를 x + 1로 설정
    candidate = x + 1
    # 후보가 조건을 만족할 때까지 반복
    while count_diff_bits(x, candidate) > 2:
        # 조건을 만족하지 않으면 후보를 1 증가시킴
        candidate += 1
    # 조건을 만족하는 첫 번째 후보를 반환
    return candidate

# 주어진 리스트 numbers의 각 수에 대해 f(x) 값을 계산하여 반환
def solution(numbers):
    # 각 숫자에 대해 find_f를 호출하여 결과 리스트를 만듦
    return [find_f(number) for number in numbers]

2. 검색을 하다가 비트의 차이는 짝수와 홀수에서 규칙이 있다는 것을 보고,
   코드를 따서 정리하고 제출.

def solution(numbers):
    result = []
    for number in numbers:
        if number % 2 == 0:
            # 짝수인 경우 다음 숫자는 항상 비트가 1개 다름
            result.append(number + 1)
        else:
            # 홀수인 경우
            # 1. 0을 만날 때까지 오른쪽 비트로 이동
            # 2. 0을 1로 바꾸고 그 오른쪽 비트를 0으로 변경
            bits = list(bin(number)[2:])
            bits = ['0'] + bits  # 앞에 0을 추가하여 모든 경우를 포괄
            for i in range(len(bits)-1, -1, -1):
                if bits[i] == '0':
                    bits[i] = '1'
                    if i + 1 < len(bits):
                        bits[i + 1] = '0'
                    break
            new_number = int(''.join(bits), 2)
            result.append(new_number)
    return result

어렵다...

---

✔️ CHECK POINT

• SQL

  • 계층적 구조 트리
    

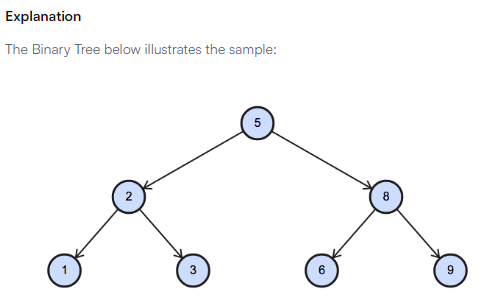
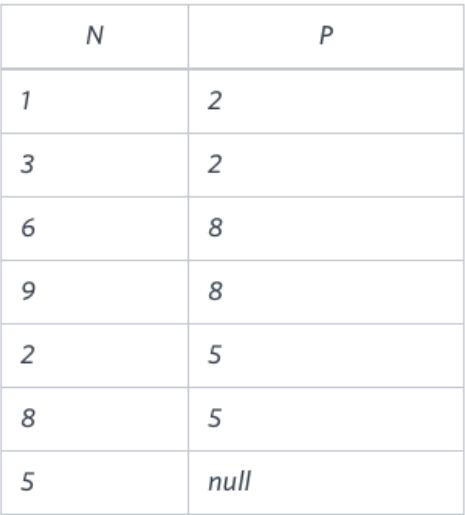
    # 뿌리, 가지, 잎 구조 이해하고 쿼리 작성하기
    SELECT DISTINCT(N),
           CASE WHEN P IS NULL THEN 'Root'
                WHEN N IN(SELECT DISTINCT(P) FROM BST) THEN 'Inner'
                ELSE 'Leaf' 
                END BT
    FROM BST
    ORDER BY N

• PYTHON

  • bin() 함수 : 숫자를 비트로 변환하는 함수.
    결과를 0b1001 과 같이 반환하기 때문에 비트만 확인하려면,
    bin(number)[2:] 와 같은 슬라이싱이 필요.

  • XOR 연산( ^ 연산자) : 두 비트가 다를 때 결과가 1이 되는 비트 연산.
    예시) bin(5 ^ 3).count('1') = 5와 3의 XOR 연산 후 1의 갯수 :
    5의 이진수 표현: 0101
    3의 이진수 표현: 0011
    XOR 결과: 0110
    이 결과에서 '1'의 개수는 2개

---

1. 비트 차이 개수를 계산하는 함수를 생성하고,
   X 보다 큰 숫자를 하나씩 비교하면서 비트 차이가 2개 이하일 때 그 숫자를 반환하는 함수로
   코드를 제출했는데, 테스트 케이스 중 시간 초과로 통과되지 않았다.

# 두 숫자 a와 b 사이의 비트 차이 개수를 계산하는 함수 생성
def count_diff_bits(a, b):
    # XOR 연산을 통해 두 숫자의 비트가 다른 위치 찾기
    xor_result = a ^ b
    # XOR 결과를 이진수 문자열로 변환
    binary_representation = bin(xor_result)
    # 이진수 문자열에서 '1'의 개수를 셈
    diff_bits = binary_representation.count('1')
    # 두 숫자 간의 비트 차이 개수를 반환
    return diff_bits

# x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수를 찾는 함수 생성
def find_f(x):
    # x보다 큰 수를 찾기 위해 초기 후보를 x + 1로 설정
    candidate = x + 1
    # 후보가 조건을 만족할 때까지 반복
    while count_diff_bits(x, candidate) > 2:
        # 조건을 만족하지 않으면 후보를 1 증가시킴
        candidate += 1
    # 조건을 만족하는 첫 번째 후보를 반환
    return candidate

# 주어진 리스트 numbers의 각 수에 대해 f(x) 값을 계산하여 반환
def solution(numbers):
    # 각 숫자에 대해 find_f를 호출하여 결과 리스트를 만듦
    return [find_f(number) for number in numbers]

2. 검색을 하다가 비트의 차이는 짝수와 홀수에서 규칙이 있다는 것을 보고,
   코드를 따서 정리하고 제출.

def solution(numbers):
    result = []
    for number in numbers:
        if number % 2 == 0:
            # 짝수인 경우 다음 숫자는 항상 비트가 1개 다름
            result.append(number + 1)
        else:
            # 홀수인 경우
            # 1. 0을 만날 때까지 오른쪽 비트로 이동
            # 2. 0을 1로 바꾸고 그 오른쪽 비트를 0으로 변경
            bits = list(bin(number)[2:])
            bits = ['0'] + bits  # 앞에 0을 추가하여 모든 경우를 포괄
            for i in range(len(bits)-1, -1, -1):
                if bits[i] == '0':
                    bits[i] = '1'
                    if i + 1 < len(bits):
                        bits[i + 1] = '0'
                    break
            new_number = int(''.join(bits), 2)
            result.append(new_number)
    return result

어렵다...

---