TIL(24.06.23.)

---

#INTRO

주말 좋다 : )

편안.

---

#코드카타

• KATA #71

• SQL

  • 맨해튼 거리 :

  • 맨해튼 거리는 두 점 사이의 거리로,
    각 좌표 축을 따라 이동하는 거리의 합으로 계산,
    체스판 위에서 룩이 이동하는 방식과 유사하다.

    두 점 ( P_1(x_1, y_1) )과 ( P_2(x_2, y_2) ) 사이의 맨해튼 거리 :
    D Manhattan​ =
∣ x 1​ − x 2​ ∣ + ∣ y 1​ − y 2​ ∣

  • ABS() 절댓값 함수

    # 단순 연산
    SELECT ROUND(
    		 ABS(
             MIN(LAT_N) - MAX(LAT_N)
             ) + 
             ABS(
             MIN(LONG_W) - MAX(LONG_W)
             ), 4)
    FROM STATION

  • 유클리드 거리 :

  • 유클리드 거리는 두 점 사이의 직선 거리를 나타내며,
    피타고라스의 정리를 사용하여 계산한다.

    두 점 ( P_1(x_1, y_1) )과 ( P_2(x_2, y_2) ) 사이의 유클리드 거리 :
    D Euclidean​ =
( ( x 1​ − x 2​ ) ** 2 + ( y 1​ − y 2​ ) ** 2 ) ** 0.5

  • SQRT() 제곱근 함수 , POWER() 제곱 함수

    # 단순 연산
    SELECT ROUND(SQRT(POWER((A - B), 2) + POWER((C-D), 2)), 4)
    FROM ( 
          SELECT MAX(LAT_N) A
               , MIN(LAT_N) B
               , MAX(LONG_W) C
               , MIN(LONG_W) D 
          FROM STATION
          ) AS  DISTANCE_POINT

---

#프로젝트 정리

• 발표자료 기획, 컨텐츠 정리

분석 과정 비교 내용 정리

분석 1 : 이상치 제거 X

변수 선택
데이터 표준화(스탠다드)
PCA 분석(주성분 4개)
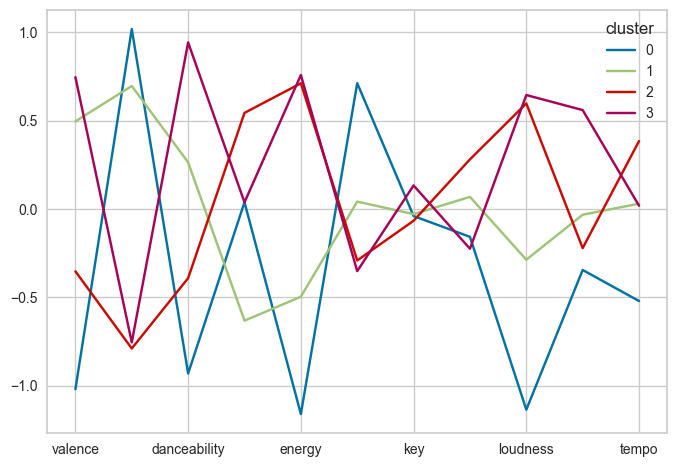
군집 분석 (K-means ; K 값 4개)
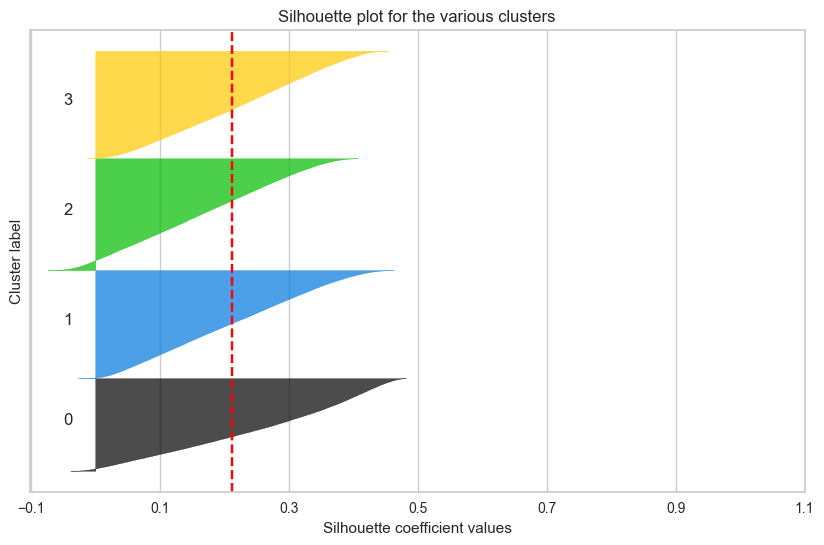
실루엣 계수 계산(0.235)

---

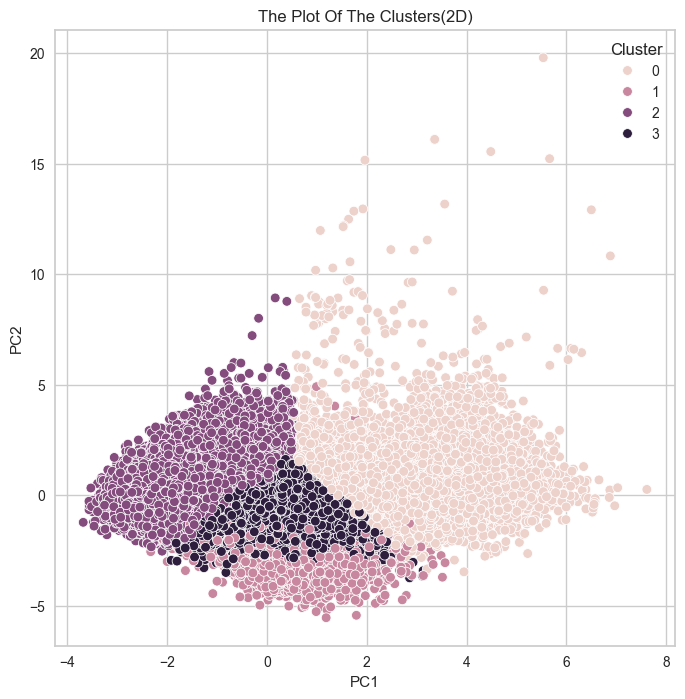
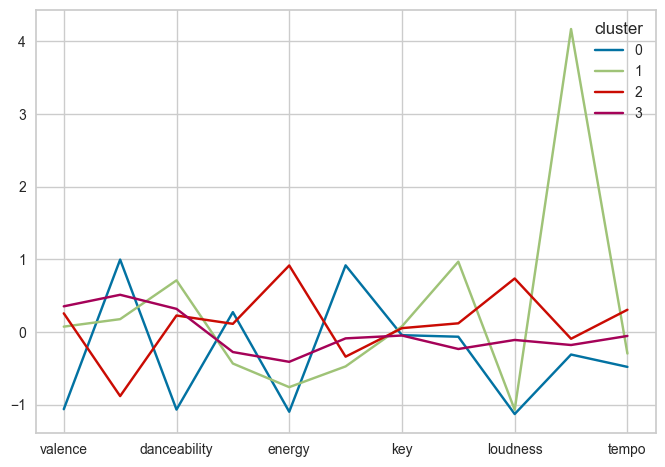
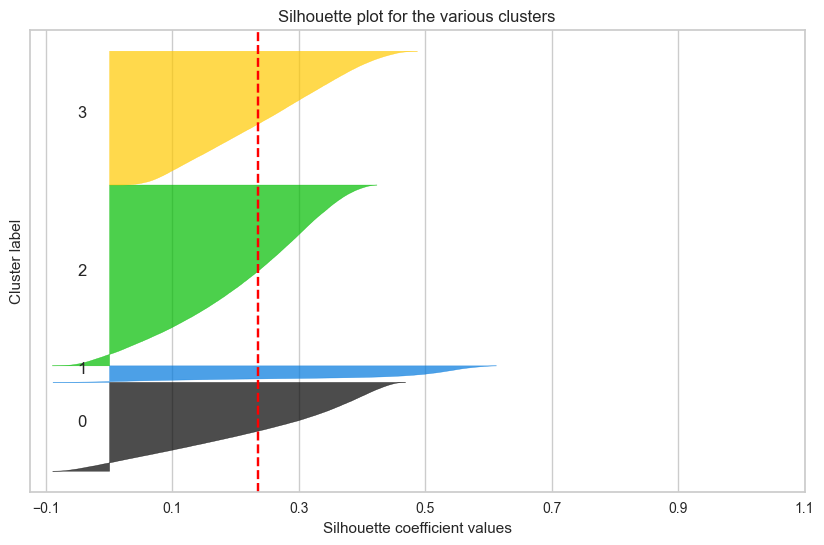
분석 2 : 이상치 제거 O

변수 선택
이상치 제거(Isolation Forest ; 약 20% 행 제거)
데이터 표준화(스탠다드)
PCA 분석(주성분 4개 ; 설명력 0.60)
군집 분석 (K-means ; K 값 4개)
실루엣 계수 계산(0.212)

---

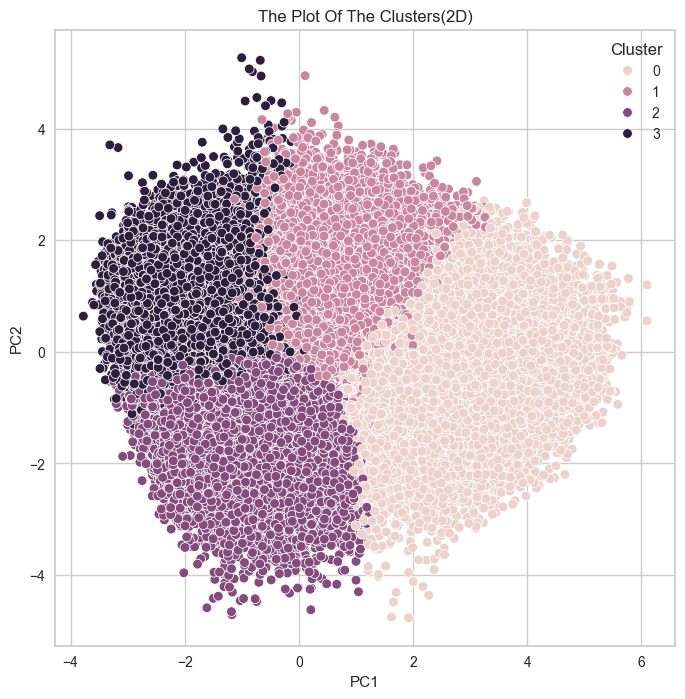
#OUTRO

오늘의 한 줄.

프로젝트까지 잘 마무리 해보자 !