알고리즘 이론 - 카운팅 정렬

카운팅 정렬(Counting Sort)

• 카운팅 정렬은 계수 정렬이라고도 한다.
• 카운팅 정렬은 정수로 이루어진 리스트만 정렬이 가능하다. 리스트의 정수의 값을 인덱스로 활용하는 방법을 사용하기 때문이다.
• 그러므로, 값이 인덱스가 되기 위해서는 리스트 안의 최대값을 알아야 그 크기에 맞는 새로운 리스트를 선언해 줄 수 있다.
• 0~100점 사이인 학생들의 성적과 같이 중복되는 값이 발생하는 리스트의 정렬에 좋음. 만약 값 차이가 많이나서 값이 0 ~ 100000 사이인 배열이라면 공간을 많이 차지할 수 있다.

사실 이해하기 처음엔 매우 어려울 수 있다. 과정은 다음과 같다.

1. 배열 안의 가장 큰 수만큼의 크기의 리스트 c를 생성 후 0을 전부 할당.
2. 순서대로 초기 입력받은 리스트 arr에 있는 중복된 수의 개수만큼 arr의 값에 해당하는 인덱스에 할당.
   ex) arr[1] = 9 arr[10] = 9 였으면 9가 두 번 나왔으므로, c[9] = 2가 되는 것이다.
3. 리스트 c 값들의 누적합을 저장해가며 구한다.
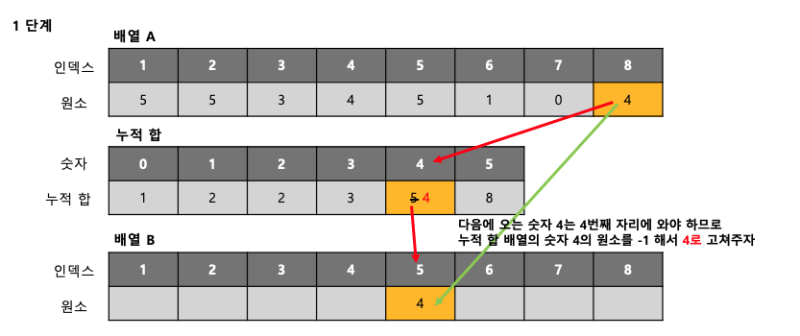
4. arr와 같은 크기의 sorted_arr를 생성해 arr에서 순서대로 나온 값들이 c의 인덱스 값이 되고, c의 인덱스 안의 값 -1 은 새로운 sorted_arr의 인덱스가 된다. 그리고 중복된 값이 arr에 있을 수 있으니 호출된 c의 인덱스를 1씩 감소시켜 줘야만 중복 값도 출력이 된다.

#카운팅 정렬
def counting_sorted(arr, K): #arr는 배열, K는 arr에 들어갈 수 있는 숫자들의 최대값이다. K는 arr의 요소들 중에 가장 큰 값 이상이어야만 한다.
    c = [0] * K # arr안에 포함될 수 있는 최대값 크기의 리스트 c를 생성하고 0을 할당한다.
    sorted_arr = [0] * len(arr) # 정렬된 arr를 저장하기위한 sorted_arr 리스트 생성.
    
    for i in arr: 
        c[i] += 1 # arr안의 값에 해당하는 c리스트의 인덱스에 해당 값의 개수를 할당. [0, 1, 1, 1, 1, 2, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
    
    for i in range(1,K): #[0, 1, 2, 3, 4, 6, 7, 8, 8, 9, 9, 9, 9, 9, 9, 9,....9]
        c[i] += c[i-1] #K크기의 배열이므로 K-1까지 c배열의 누적합을 구한다. 0~ K-1까지의 리스트이므로 없는 값은 0이 할당되어있다.
   
    for i in range(len(arr)): #sorted_arr[2] = 3, sorted_arr[5] = 5, sorted_arr[0] = 1 ...
        sorted_arr[c[arr[i]]-1] = arr[i] #입력받은 리스트 arr의 값을 순서대로 c를 기준으로 sorted_arr에 재배치한다.
        c[arr[i]] -= 1 # c 배열의 값을 1씩 줄여줌. 안 줄여준다면 중복을 제거해서 중복된 수의 자리가 0으로 채워져 정렬됨.

    return sorted_arr
        
arr = [3, 5, 1, 2, 9, 6, 4, 7, 5, 1, 1, 1]
print(counting_sorted(arr, 20)) # 20이 arr에 들어갈 수 있는 최대값임.

*시간복잡도는 선형 시간으로 O(N+k)이다. k는 배열에 있는 수의 최대값을 의미한다.

*효율이 좋지만 정수나 정수로 표현되는 값들을 가져야만 쓸 수 있고, 리스트의 크기가 작은데 값들의 차이가 심한 경우에는 공간 효율이 안좋다.