1. 확률분포의 정의

시작하기에 앞서, 확률분포는 무엇이고 이산/연속 확률분포는 무엇인지 먼저 살펴봅시다.

확률분포란?

확률 변수

표본 공간의 원소를 실수로 대응한 값

확률 분포 (함수)

확률 변수가 특정한 값을 가질 확률을 나타내는 함수

EX) 주사위 던지기 🎲
확률변수 ? 던졌을 때 나오는 눈 {1,2,3,4,5,6}
확률분포 ? P(x)=1/6 인 이산균등분포

📊 이산 확률 분포

• 확률 변수가 가질 수 있는 값의 개수가 셀 수 있는 (Countable) 한 확률 분포
• 확률 질량 함수 (Probability Mass Function, PMF) 로 표현
• 이산균등분포, 포아송, 베르누이, 초기하, 이항 등
• EX) 주사위 2개를 던졌을 때 두 눈의 합 S에 대한 확률 분포

기대값

본공간의 원소 $x_{i}$의 가중평균

• 가중치는 $x_{i}$ 가 나올 수 있는 확률 즉 확률질량함수 $p(xi)$

분산

이산확률변수의 분산은 평균으로부터 표본 데이터까지 거리의 제곱을 확률질량함수 p(x)
로 가중하여 더한 값

ref) 기대값과 분산의 특성

https://datascienceschool.net/02%20mathematics/07.03%20%EB%B6%84%EC%82%B0%EA%B3%BC%20%ED%91%9C%EC%A4%80%ED%8E%B8%EC%B0%A8.html

📉 연속 확률 분포

• 확률 변수가 가질 수 있는 값이 연속적인(Continuous) 확률 분포
• 확률 밀도 함수 (Probability Density Function, PDF) 로 표현
• 정규 분포, 연속 균등 분포, 카이제곱 분포, 감마 분포

기댓값

연속확률변수의 기댓값은 확률밀도함수 p(x) 를 가중치로 하여 모든 가능한 표본 x를 적분한 값

분산

평균으로부터 표본 데이터까지 거리의 제곱을 확률밀도함수 p(x)
로 가중하여 적분한 값

---

이제, 실제로 다양한 확률 분포에 대해 알아보고, 각각이 언제 어떻게 사용되는지 살펴봅시다.

확률 분포의 활용

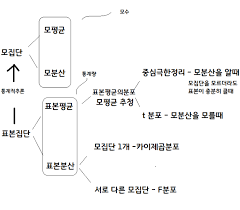
앞서 배운 많은 확률 분포를 실제로 어떻게, 어디서 사용하는가?

앞서 배웠던 통계적 추정 과정에서 우리는 모집단을 전부 조사할 수 없기에 표본을 뽑습니다.
이 표본으로 부터 "평균", "분산" 과 같은 통계량을 구하여 모집단의 평균과 분산은 이러할 것이야라고 추정하게 됩니다.

이 과정에서 확률 분포가 사용됩니다.

좀 더 자세히 보면,