피보나치 수열
1) 피보나치 수열을 출력한다. 피보나치 수열이란 앞의 2개의 수를 합하여 다음 숫자가 되는 수열이다.
2) 입력은 피보나치 수열의 총 항의 수 이다. 만약 7이 입력되면 1 1 2 3 5 8 13을 출력하면 된다.
▣ 입력설명
첫 줄에 총 항수 N(3<=N<=45)이 입력된다.
▣ 출력설명
첫 줄에 피보나치 수열을 출력합니다.
▣ 입력예제
10
▣ 출력예제
1 1 2 3 5 8 13 21 34 55
피보나치 수열 문제는 코딩 면접에서 자주 등장하는 질문 중 하나로, 이를 해결하는 방법으로 반복문과 재귀 호출 방식이 있습니다. 이 중 반복문을 사용하는 방법이 재귀 호출보다 훨씬 효율적입니다. 그 이유는 재귀 호출 방식은 호출할 때마다 스택에 메서드 호출이 쌓이면서, 메모리와 처리 시간 측면에서 추가적인 오버헤드가 발생하기 때문입니다. 반면, 반복문은 이러한 오버헤드 없이 순차적으로 계산을 수행하므로, 속도와 메모리 사용 면에서 더 빠르고 효율적입니다.
반복문
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i = 1; i <= n; i++){
System.out.print(fibo(i)+" ");
}
}
public static int fibo(int n){
if(n == 1 || n == 2){
return 1;
}
int a = 1;
int b = 1;
int result = 0;
for(int i = 3; i <= n; i++){
result = a + b;
a = b;
b = result;
}
return result;
}실행시간
---------
1600ms재귀호출
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i = 1; i <= n; i++){
System.out.print(fib(i)+" ");
}
}
public static int fib(int n){
if(n == 1) return 1;
else if(n == 2) return 1;
else{
return fib(n-2) + fib(n-1);
}
}
실행시간
---------
7298ms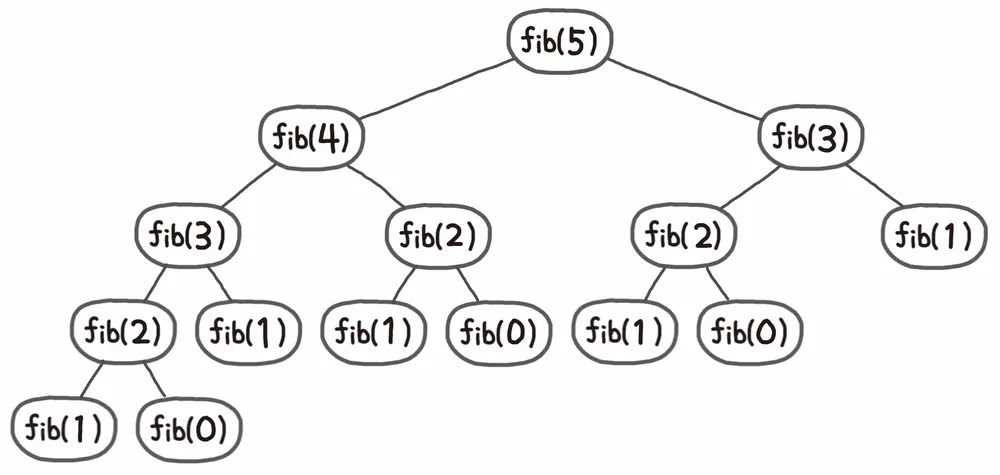
위와 같이 5번째 피보나치 수열을 구하는 데 함수 fibo를 호출하는 횟수는 총 15번이다. 위의 예시에서 중복해서 계산하는 값만 따져 봐도 fib(3)이 2번, fib(2)가 3번, fib(1)을 5번, fib(0)을 3번 계산한다. 15번의 계산 중에 무려 11번을 중복해서 계산하는 셈이다. 비록 위 예시는 비교적 작은 값을 제시했지만, 피보나치 수열을 값이 커지면 시간 복잡도는 피보나치 수열의 값에 따라 폭발적으로 증가한다.
재귀호출-(메모이제이션)
메모이제이션 사용:
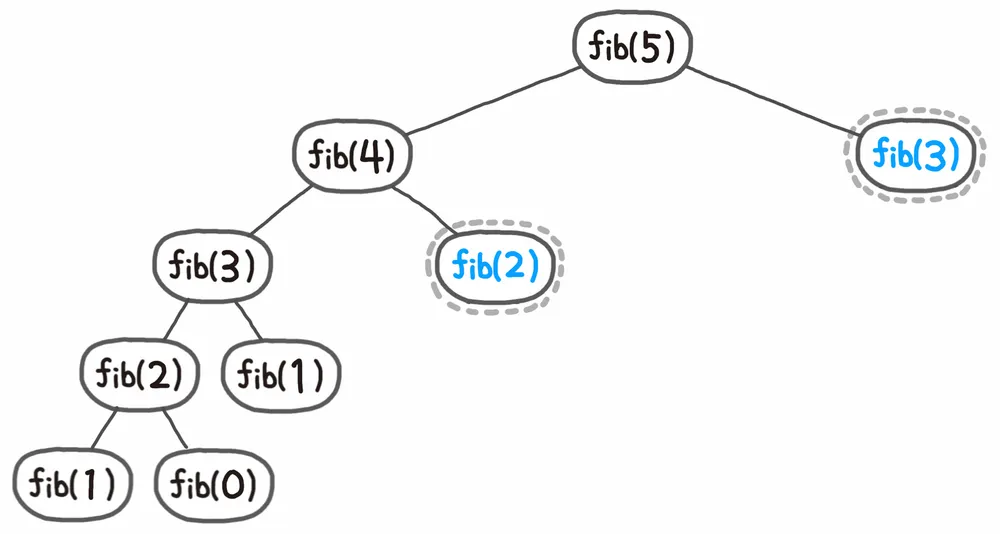
FIB_MEMORY 배열을 사용해 이미 계산된 피보나치 수를 저장하고, 동일한 계산이 필요할 때는 저장된 값을 재사용합니다. 이를 통해 중복 계산을 피하며, 특히 큰 n 값에 대해 효율적으로 피보나치 수를 계산을 합니다. 예를 들어 fib(5)를 계산할 때, fib(4)와 fib(3)을 계산한 결과를 저장해 두고, 이후 다시 호출할 때는 재사용합니다.
재귀 호출 최적화:
각 피보나치 수를 한 번만 계산하므로, 재귀 호출의 깊이가 줄어들고, 계산 속도가 빠릅니다.
피보나치 수열을 계산하는 데 있어 중복되는 연산이 대폭 줄어들기 때문에 성능이 크게 향상됩니다.
public class Main {
static int[] FIBO_MEMORY;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
FIBO_MEMORY = new int[n+1];
fibo(n);
for(int i = 1; i <= n; i++){
System.out.print(FIBO_MEMORY[i]+" ");
}
System.out.println();
}
public static int fibo(int n){
if(FIBO_MEMORY[n] > 0) return FIBO_MEMORY[n];
if(n == 1) return FIBO_MEMORY[n] = 1;
else if(n == 2) return FIBO_MEMORY[n] = 1;
else{
return FIBO_MEMORY[n] = fibo(n-2) + fibo(n-1);
}
}
}
실행시간
---------
980ms여기서 알 수 있는 점은, 일반적으로 반복문이 재귀 호출보다 효율적인 경우가 많은데 메모이제이션을 사용한 재귀 호출의 경우에는 더 나은 성능을 보일 수 있다라는 점을 알 수 있었습니다.
