DP (동적 계획법)
오늘은 동적 계획법에 대해 설명하도록 하겠습니다. 자료구조의 동적할당에서 '동적'은 '프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법' 라고 하는데 너무 어려운 말은 두고, 그냥 기억하는 알고리즘이라고 생각하면 편합니다.
대표적인 예시로 단순 재귀 문제인 피보나치 수열이 있는데 F(n) = F(n-1) + F(n-2)
static int fibo(int x){
if(x == 1 || x == 2) return 1;
return fibo(x-1)+fibo(x-2);
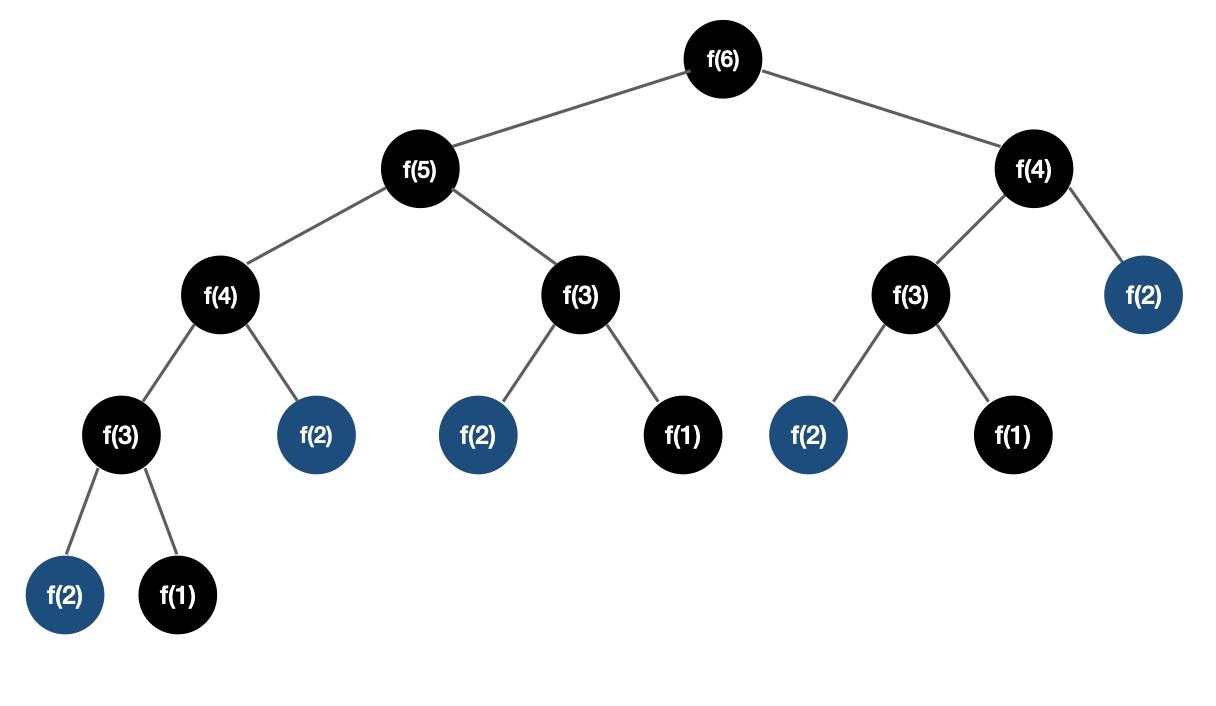
위와 같이 함수를 호출을 하면 시간복잡도 O(2^n) 을 갖게 됩니다. 딱 보기에도, 같은 함수를 여러번 중복 호출해서 효율이 안 좋아 보입니다.
이때, 좀 더 효율적으로 사용 할 방법이 있는가 ?
이 의문에 답으로 DP가 등장...! 우선, DP문제가 성립 하는 조건을 알아봅시다.
1. 최적 부분 구조 - 상위 문제를 하위문제로 나눌 수 있으며, 하위 문제의 답을 모아서 상위 문제를 해결 할 수 있다.
2. 중복되는 문제 - 동일한 작은 문제를 반복적으로 해결해야 한다.
이러한 조건을 봤을때, 피보나치 수열은 DP를 사용 할 수 있다!
DP의 구현 방법은 일반적으로 두 가지 방식, Top-down(하향식) 과 Bottom-up(상향식) 으로 구현 합니다.
Top-down(하향식)
의미 그대로 상위 문제를 해결하기 위해서 하위문제를 재귀적으로 호출하여 하위 문제를 해결함으로써 상위 문제를 해결하는 방식 입니다. 이때 Memoization이 사용됩니다.
static int fibo(int x){
if(x==1 || x==2) return 1;
if(dp[x] != 0) return dp[x];
dp[x] = fibo(x-1) + fibo(x-2);
return dp[x];
}Bottom-up(하향식)
하위에서부터 문제를 해결해나가면서 먼저 계산했던 문제들의 값을 활용해서 상위 문제를 해결하는 방식입니다.
static int fibo(int x){
dp[1]=1;
dp[2]=1;
for(int i = 3; i < x+1; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[x];
}
풀어보면 좋은 문제 !
1. 계단 오르기
철수는 계단을 오를 때 한 번에 한 계단 또는 두 계단씩 올라간다. 만약 총 4계단을 오른다면 그 방법의 수는
1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2 로 5가지이다.
그렇다면 총 N계단일 때 철수가 올라갈 수 있는 방법의 수는 몇 가지인가?
| 예시 입력 1 | 예시 출력 1 |
|---|---|
| 7 | 21 |
계단을 1칸 또는 2칸씩 올라갈 수 있는 상황에서, 각 계단에 도달하는 방법의 수를 구하는 문제는 동적 계획법(DP)을 이해하기에 적절한 문제라고 생각합니다 !
아이디어 !
1번째 계단에 도달하는 방법: 한 번에 1칸 올라가는 방법이므로 방법은 1가지.
2번째 계단에 도달하는 방법: 1칸씩 두 번 올라가는 방법 (1,1)과, 2칸을 한 번에 올라가는 방법 (2)가 있으므로, 총 2가지.
3번째 계단에 도달하는 방법:
- 1번째 계단에서 2칸을 올라가는 방법
- 2번째 계단에서 1칸을 올라가는 방법
이를 통해 첫 번째 계단에서 세 번째 계단까지 가는 방법과 두 번째 계단에서 세 번째 계단까지 가는 방법을 더하면 됩니다. 이를 통해 다음과 같은 점화식을 유추 할 수 있습니다.
dp[i] = dp[i-1] + dp[i-2]
그리고 이것을 활용하여 코드를 작성해 보면
import java.util.*;
public class DP{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// dp 배열 생성
int[] dp = new int[n+1];
//
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= n; i++){
dp[i] = dp[i-2] + dp[i-1];
}
System.out.println(dp[n]);
}
}2. 최대 부분 증가수열
N개의 자연수로 이루어진 수열이 주어졌을 때, 그 중에서 가장 길게 증가하는(작은 수에서 큰 수로) 원소들의 집합을 찾는 프로그램을 작성하라.
예를 들어, 원소가 2, 7, 5, 8, 6, 4, 7, 12, 3 이면 가장 길게 증가하도록 원소들을 차례대로 뽑아내면 2, 5, 6, 7, 12를 뽑아내어
길이가 5인 최대 부분 증가수열을 만들 수 있다.
| 예시 입력 1 | 예시 출력 1 |
|---|---|
| 8 | |
| 5 3 7 8 6 2 9 4 | 4 |
아이디어 !
위에 문제는 너무 기초 문제였고 이 문제는 조금 고민을 해봐야 한다. 우선, DP문제는 큰 문제를 작은 문제로 나누어 푸는 것인데. 이 문제는 최적의 해를 구하기 위해 부분 문제를 반복해서 해결하고, 이미 계산한 부분 문제의 결과를 재사용 하여 중복 계산도 방지를 함으로써 DP적 사고로 접근을 해야한다. !
DP 배열을 어떻게 설정할 것인가가 이 문제의 포인트인데, 입력 데이터가 arr 배열에 주어졌을 때, dp[i]는 arr[i]로 끝나는 수열의 최대 길이로 저장하도록 하려 합니다. 예를 들어, arr[2]가 7이라면, dp[2]는 arr[2]로 끝나는 부분 수열 중에서 가장 긴 수열의 길이를 저장합니다. 즉, arr[2] = 7일 때 가능한 수열은 (5, 7), (3, 7), (7)과 같이 여러 가지가 있을 수 있지만, 이 중 최대 길이는 2이므로 dp[2]에는 2가 저장됩니다. 이를 통해 여기에서도 점화식을 구할 수 있는데
바로 dp[i] = max(dp[i],dp[j]+1) 입니다. 이를 통해 코드를 작성해 보겠습니다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
int[] dp = new int[n];
dp[0] = 1;
int result = 0;
for (int i = 1; i < n; i++) {
int max = 0;
// i기준으로 왼쪽으로 탐색
for (int j = i - 1; j >= 0; j--) {
// 기준보다 작으면서, 여태까지 수열의 길이가 가장 큰 값을 찾기
if (arr[j] < arr[i] && dp[j] > max) {
max = dp[j];
}
}
// +1 을 해주는 이유가 길이이기 때문에 여태까지 긴 길이에 자기 자신 1개만 추가하면 되니깐 +1을 해줍니다.
dp[i] = max + 1;
result = Math.max(result, dp[i]);
}
System.out.println(result);
}
}
