이분 탐색(Binary Search)
오늘의 알고리즘 !!! 이분 탐색 입니다.
이분탐색은 정렬된 배열에서 특정 숫자의 위치를 찾는데 유용합니다.
이분탐색은 정렬된 테이터에서 특정 값을 효율적으로 찾기 위해 사용을 하는데요, 주어진 배열이 정렬되어 있다는 전제 아래, 데이터를 절반씩 나누면서 목표 값을 빠르게 찾아가느 방식 입니다.
굳이 왜 이분 탐색을 쓰죠?
탐색 시간의 단축 : 단순히 모든 값을 순차적으로 탐색하는 선형 탐색은 데이터가 많을 때 시간이 많이 거립니다. 반면 이분 탐색은 데이터의 양이 늘어나더라도 검색 시간을 크게 줄여줍니다. 무려, 시간 복잡도 O(log N) 입니다. 그 말은 1,000,000개의 데이터도 대략 20번만의 비교로 값을 찾을 수 있다는 말이죠.
이제 이분탐색을 이해하기 좋았던 문제를 통해 알아보도록 하겠습니다.
문제 1 )
임의의 N개의 숫자가 입력으로 주어집니다. N개의 수 중 한 개의 수인 M이 주어지면
몇 번째에 있는지 구하는 프로그램을 작성하세요. 단 중복값은 존재하지 않습니다.
문제 조건:
1. 첫 줄에 자연수 N과 M이 주어집니다. 3 <= N <= 100,000,000, M은 배열에서 찾고자 하는 수입니다.
2. 두 번째 줄에 N개의 정수가 공백으로 구분되어 주어집니다.
3. 시간 제한은 500ms입니다.| 입력 |
|---|
| 8 32 |
| 23 87 65 12 57 32 99 81 |
여기서 보면, 시간 제한이 500ms로 매우 짧다라는 것을 볼 수 있습니다. 그리고 N이 100,000,000이 최대로 선형적으로 찾아보면 시간이 부족하다라고 생각을 할 수 있습니다. 그러면 여기서 필요한게 뭐다? 이분 탐색입니다. 그래서 선형적으로 말고 이분탐색을 이용해서 찾아보도록 하겠습니다!
1. 배열을 정렬한다.
2. lt를 0, rt를 배열의 끝으로 설정한다.
3. 가운데 값(mid)을 구해 찾고자 하는 값과 비교하고, 값에 따라 lt 또는 rt를 조정한다.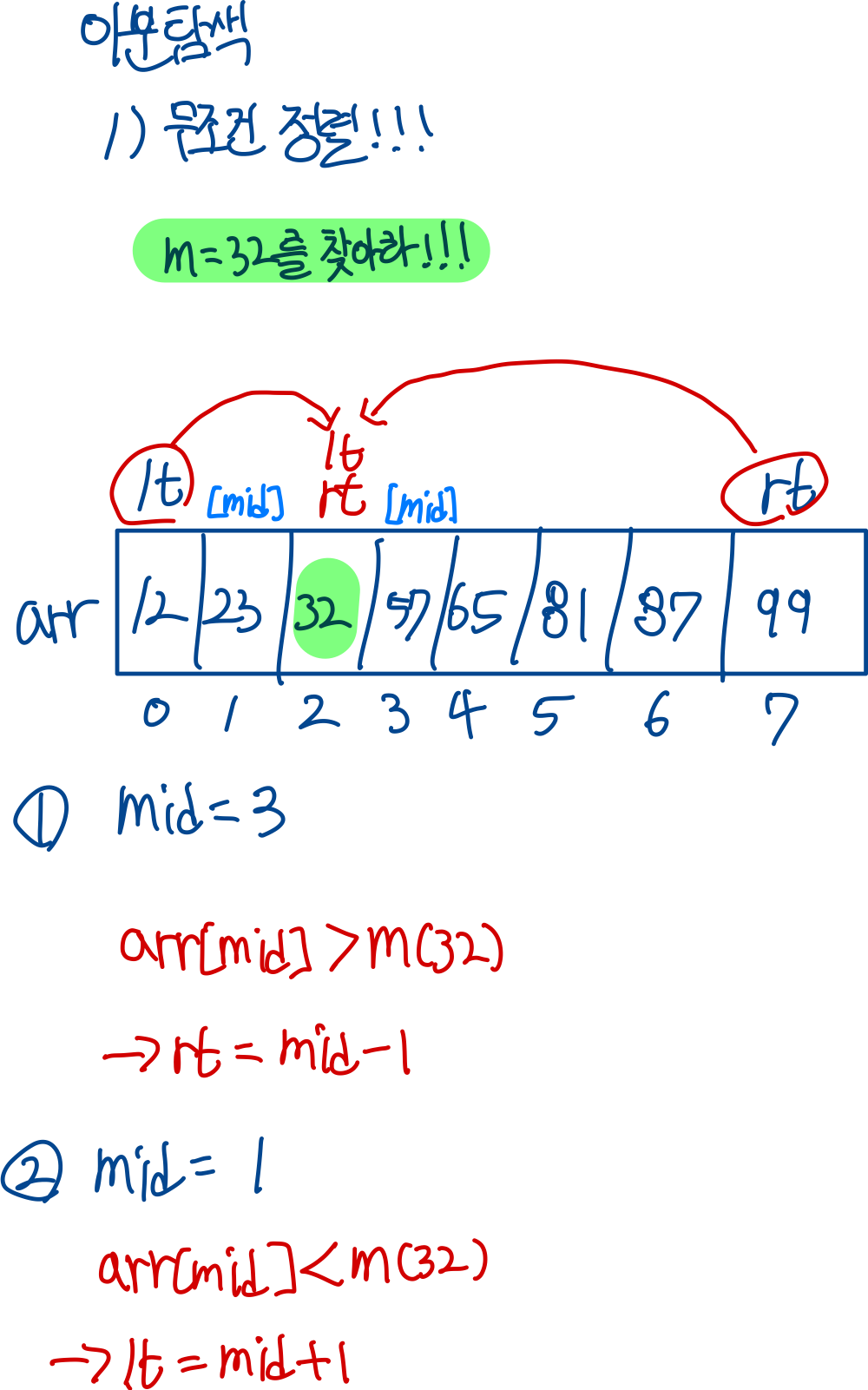
문제 2)
백준 - 10816
숫자 카드는 정수 하나가 적혀져 있는 카드이다. 상근이는 숫자 카드 N개를 가지고 있다. 정수 M개가 주어졌을 때, 이 수가 적혀있는 숫자 카드를 상근이가 몇 개 가지고 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.
셋째 줄에는 M(1 ≤ M ≤ 500,000)이 주어진다. 넷째 줄에는 상근이가 몇 개 가지고 있는 숫자 카드인지 구해야 할 M개의 정수가 주어지며, 이 수는 공백으로 구분되어져 있다. 이 수도 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.
출력
첫째 줄에 입력으로 주어진 M개의 수에 대해서, 각 수가 적힌 숫자 카드를 상근이가 몇 개 가지고 있는지를 공백으로 구분해 출력한다.
| 입력 | 출력 |
|---|---|
| 10 | 3 0 0 1 2 0 0 2 |
| 6 3 2 10 10 10 -10 -10 7 3 | |
| 8 | |
| 10 9 -5 2 3 4 5 -10 |
풀이
우선 브루트포스 접근 시 각 카드 숫자마다 카드 전체를 확인해야 하므로, 시간 복잡도가 (N*M) 으로 최대 2500억 정도의 연산이 필요하므로 시간 제한을 초과하게 됩니다. 따라서 이분탐색 이나 해시맵 을 통해 풀 수 있는데 저는 이분탐색을 이용해 풀어보도록 하겠습니다.
이분 탐색을 활용해 특정 값의 개수를 구하는 방법으로, 값이 처음 등장하는 위치 와 마지막으로 등장하는 위치 를 찾는 것입니다. 저는 이를 lowerBound, uppderBound 함수로 표현했습니다.
- lowerBound : 찾고자 하는 key값이 처음 등장하는 위치의 인덱스 를 반환.
- upperBound : 찾고자 하는 key 값보다 큰 값이 처음 등장하는 위치의 인덱스 를 반환.
- 정답 : uppderBound - lowerBound.
각 숫자에 대한 출력을 위해 StringBuilder 를 이용했습니다.
int m = sc.nextInt();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < m; i++) {
int key = sc.nextInt();
sb.append(upperBound(arr, key) - lowerBound(arr, key)).append(' ');
}
System.out.println(sb);
upperBound 메서드
- key가 arr[mid] 보다 작다면, rt를 mid - 1로 이동해 더 작은 범위로 좁힙니다.
- 그렇지 않다면 lt 를 mid + 1로 이동하여 오른쪽 탐색을 합니다.
- 반복이 끝나면 rt는 key보다 큰 값이 처음으로 등장하는 위치를 반환 합니다.
private static int upperBound(int[] arr, int key) {
int lt = 0;
int rt = arr.length - 1;
while (lt <= rt) {
int mid = (lt + rt) / 2;
if (key < arr[mid]) {
rt = mid - 1;
} else {
lt = mid + 1;
}
}
return lt;
}
lowerBound 메서드
- 만약 key가 arr[mid]보다 작거나 같으면 rt를 mid - 1로 줄여, key의 왼쪽 범위를 탐색합니다.
- 그렇지 않으면 lt를 mid + 1로 늘려, key의 오른쪽 범위를 탐색합니다.
- 최종적으로 lt는 key가 배열에서 처음 나타나는 위치가 됩니다.
private static int lowerBound(int[] arr, int key) {
int lt = 0;
int rt = arr.length - 1;
while (lt <= rt) {
int mid = (lt + rt) / 2;
if (key <= arr[mid]) {
rt = mid - 1;
} else {
lt = mid + 1;
}
}
return lt;
}
