빅오표기법 (big O notaion) 이란?

일반적으로 알고리즘의 시간복잡도를 나타내는데 사용된다. Big-O 표기법은 알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도를 가진다는 의미이다. 물론 공간복잡도에 대해서도 사용될 수 있다.
어떤 함수의 성능을 측정하는 표기하는 방식이다.

시간복잡도(Time complexity)

알고리즘의 실행시간을 측정하여 표현하는 방식입니다.
동일한 출력값을 가지는 알고리즘의 실행 속도가 어느 한쪽이 적게든다면 그 알고리즘은 성능이 좋다고 말할 수 있습니다.

최상의 경우 : 오메가 표기법 (Big-Ω Notation)
평균의 경우 : 세타 표기법 (Big-θ Notation)
최악의 경우 : 빅오 표기법 (Big-O Notation)

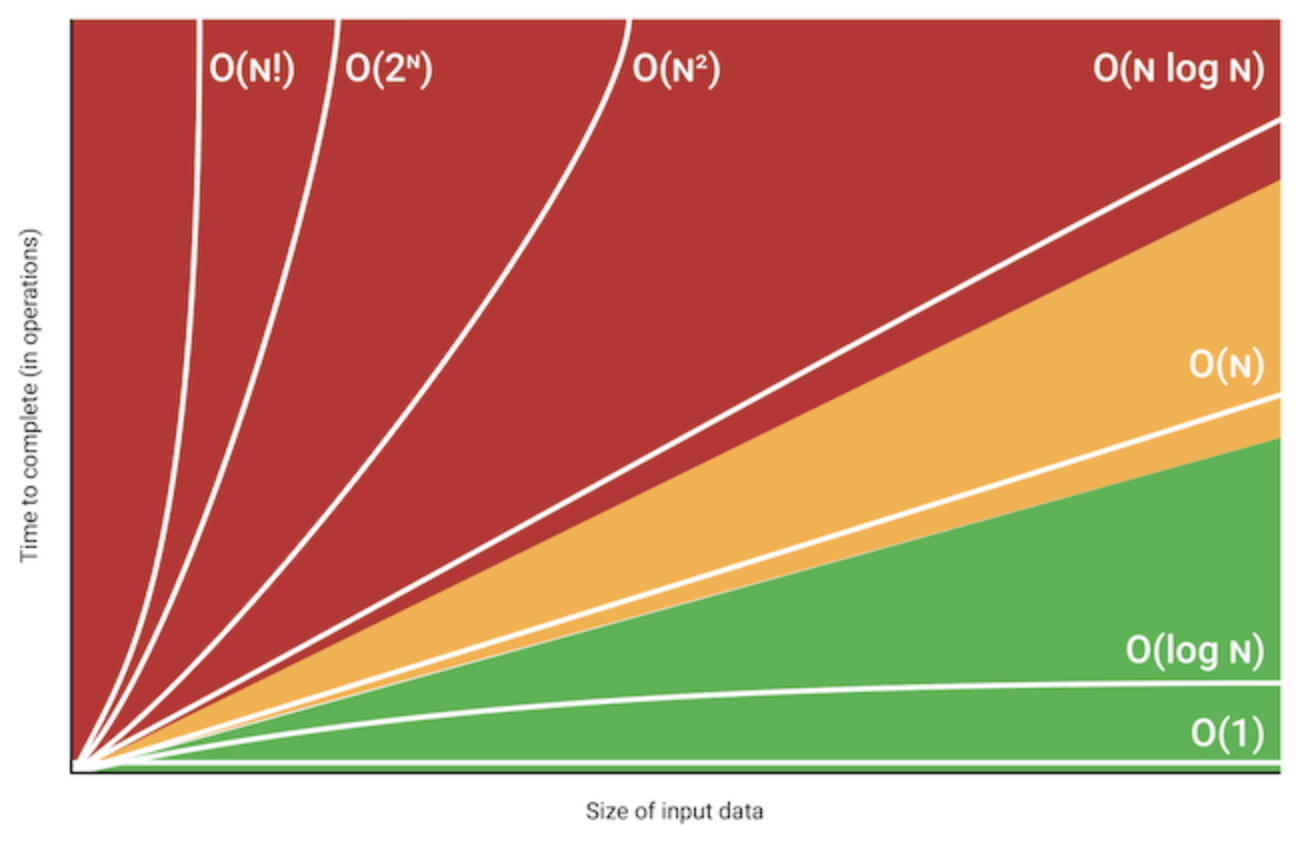
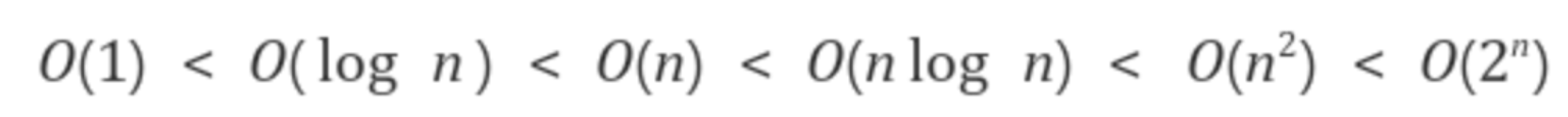
O(1) 상수 시간

입력된 데이터의 크기에 상관없이 일정한 시간이 걸리는 알고리즘.

const array = [1,2,3,4,5,6];
const findValueByIndex = (index) =>{
	return array[index];
}
console.log(findValueByIndex(2));
//3

O(log n) 로그 시간

알고리즘 진행 시 특정 조건에서 시간이 줄어든다.
BST(Binary Search Tree)에서 유망하지 않는 데이터가 있으면 가지치기를 하면서 시간을 단축하는 것이 대표적이다.

function binarySearch(items, match) {
  let low = 0
  let high = items.length -1;

  while (low <= high) {
     mid = parseInt((low + high) / 2);
     current = items[mid];
     if (current > match) {
        high = mid - 1;
     } else if (current < match) {
        low = mid + 1;
     } else {
        return mid;
     }   
  }       
  return -1;
}
let arr = [ 1,2,3,4,5];
let item = 2;
console.log(binarySearch(arr,item))

O(n) Linear

입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘이다. 예를 들어 데이터가 10배가 되면, 처리 시간도 10배가 된다. 선형 탐색 알고리즘이 대표적이다.

const arr = [1,2,3,4];
for(let i = 0 ; i < arr.length ; i++){
  console.log(arr[i]);
}

O(n log n)

데이터가 많아질수록 처리시간이 로그(log) 배 만큼 더 늘어나는 알고리즘이다. 예를 들어 데이터가 10배가 되면, 처리 시간은 약 20배가 된다. 정렬 알고리즘 Merge sort, Quick sort의 평균 시간 복잡도이다.

O(n²) (quadratic)

데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘이다. 예를 들어 데이터가 10배가 되면, 처리 시간은 최대 100배가 된다. 이중 루프(n² matrix)가 대표적이다. 단, m이 n보다 작을 때는 반드시 O(nm)로 표시하는것이 바람직하다.

const arr1 = [1,2,3,4];
const arr2 = [5,6,7,8];
for(let i = 0 ; i < arr1.length ; i ++){
  for(let j = 0 ; j < arr2.length ; j++){
    console.log(arr1[i] + arr2[j]);
  }
}

O(2ⁿ) (Exponential)

데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘이다. 대표적으로 피보나치 수열이 있으며, 재귀가 역기능을 할 경우도 해당된다.

function fibonacci(n){
  if(n <= 0) return 0;
  else if(n === 1) return 1;
  return fibonacci(n-1) + fibonacci(n-2);
}

참고: https://namu.wiki/w/%EC%A0%90%EA%B7%BC%20%ED%91%9C%EA%B8%B0%EB%B2%95
https://seolhun.github.io/contents/algorithm-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EC%9D%84-%EC%9C%84%ED%95%9C-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84-%EA%B3%84%EC%82%B0-%EB%B0%A9%EB%B2%95-big-o-%ED%91%9C%EA%B8%B0
https://velog.io/@raram2/big-o-notation-and-time-complexity