
1. 비트마스크 ?
- 비트마스크는 이진수를 사용하는 컴퓨터의 연산 방식을 이용하여, 정수의 이진 표현을 자료 구조로 사용하는 기법을 말한다.
- 이진수는 0 또는 1을 이용하므로 하나의 비트로 표현할 수 있는 경우의 수는 두 가지이다.
- 보통 어떤 비트가 1이면 "존재한다", 0이면 "존재하지않다" 라고 말할 수 있다.
2. 비트마스크의 장점
① 수행 시간이 빠르다.
비트마스크 연산은 bit 연산이기 때문에 O(1)에 구현되는 것이 많다. 따라서 다른 자료구조를 이용하는 것보다 빠른 동작이 가능한 경우가 많다. 비트의 개수만큼 원소를 다룰 수 있기에 연산 횟수가 늘어날수록 차이가 매우 커지게 된다.
② 메모리 사용량이 적다.
bit가 n개인 경우 각 bit당 두 가지 경우를 가지기 때문에 2ⁿ가지의 경우를 n비트 이지누 하나로 표현이 가능하다. 이처럼 하나의 정수로 매우 많은 경우의 수를 표현할 수 있기에 메모리 측면에서 효율적이다.(DP에 매우 유용하다)
3. 비트 연산자
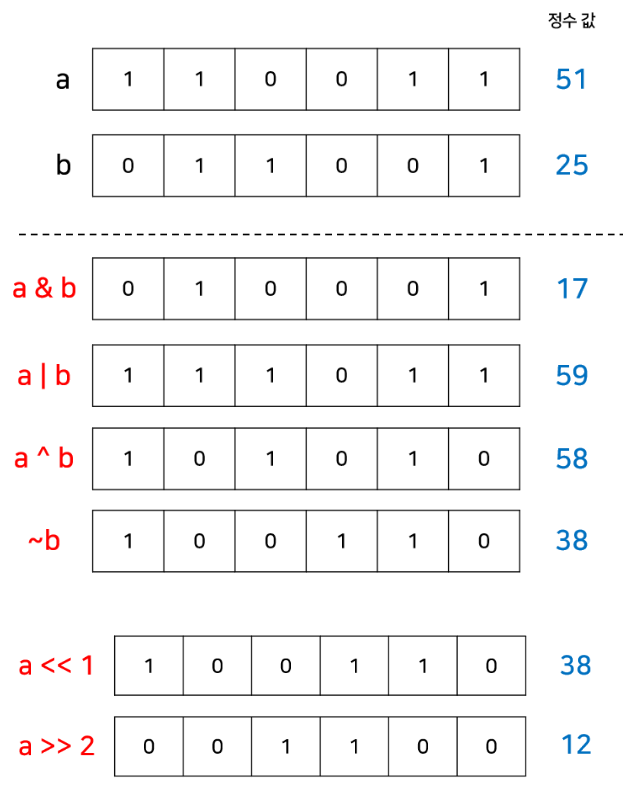
① AND연산
c = a & b두 정수 변수 a와 b를 통해서 c를 생성한다고 가정하면, a와 b를 한 bit씩 비교하면서 해당 비트가 둘 다 존재하는 경우에만 c의 해당 비트를 변경.
② OR연산
c = a | bAND연산과 같은 방식으로, 해당 비트가 둘 중 하나라도 켜져 있는 경우에 c의 해당 비트를 켠다.
③ XOR연산
c = a ^ b마찬가지로 같은 방식이며, 해당 비트가 둘 중 하나만 켜져 있는 경우에 c의 해당 비트를 켠다.
④ NOT연산
c = ~a정수 하나를 입력받아서 켜져 있는 비트는 끄고, 꺼져 있는 비트는 켠 결과를 반환한다.
⑤ Shift연산
c = (a << 1)
c = (a >> 1)시프트 연산자는 정수 a의 비트들을 왼쪽 또는 오른쪽으로 원하는 만큼 움직인다. 움직이고 나서 빈자리는 0으로 채워지게 된다. 예를 들어 13 (1101)을 오른쪽으로 1bit 움직인다고 하면, 6 (0110)이 되는 것이다.
왼쪽 시프트는 a * 2^b를 의미, 오른쪽 시프트는 a / 2^b를 의미하여 간단한 사칙연산 구현이 가능하다. (ex: (A+B) / 2 ==> (A+B) >> 1)
4. 비트마스크를 이용한 집합 구현
- n개의 비트 정수의 변수는 n개의 원소를 갖는 진합의 부분집합들을 모두 표현할 수 있다.
A라는 변수를 집합이라고 가정하고, 집합의 총원소의 개수를 10개라고 가정하겠다. (0번째 ~ 9번째 원소)
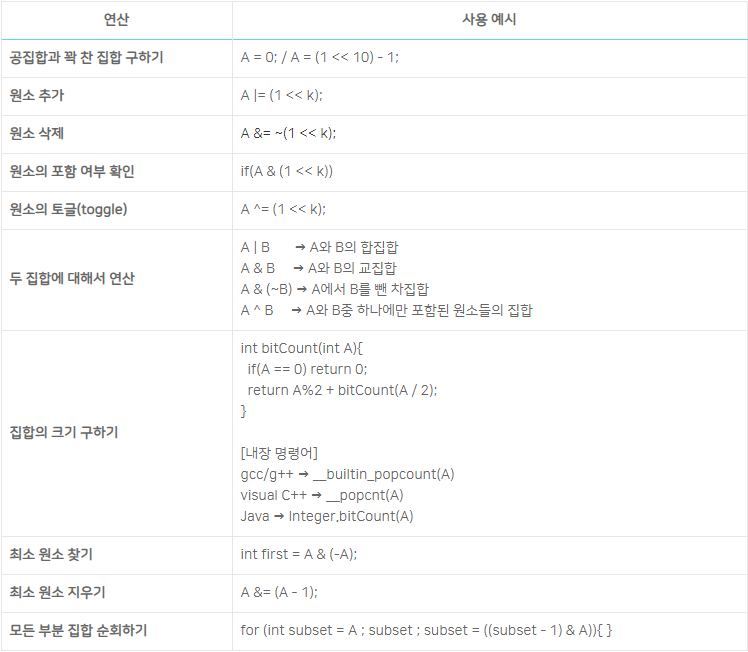
① 공집합과 꽉 찬 집합 구하기
기본적으로 공집합은 bit가 모두 꺼진 상황이기 때문에 상수 0이 공집합을 표현한다.
반대로 꽉 찬 집합은 bit가 모두 켜진 상황이기 때문에 1111111111(2) 의 값을 가져야 하는데, 이는 (1<<10) - 1 과 동일하다. 1<<10은 10000000000(2) 이므로 1을 빼면 10개의 bit가 모두 켜진 수를 얻을 수 있다.
② 원소 추가
A 집합에 특정 원소를 추가하는 방법이다. 원소에 해당하는 bit만 켜야 하기 때문에 해당 bit를 항상 1로 만드는 연산이 필요하다. 따라서 OR 연산을 이용한다.
이미 A에 원소가 포함되어 있는 경우에는 아무런 변화가 없게 된다.
③ 원소 삭제
집합에 포함된 특정 원소를 삭제하는 방법이다. 원소에 해당하는 bit가 꺼져야 하기 때문에 해당 bit를 항상 0으로 만드는 연산이 필요하다.
따라서 A -= (1<<k); 로 작성하면 된다. 하지만 이 경우는 A에 반드시 k번째 원소가 포함되어 있는 경우에만 가능하다. 만약 포함되어 있지 않은 경우에는 다른 원소의 포함 여부까지 바꿔버리기 때문이다.
그러므로 A에 k번째 원소의 포함 여부와 상관없이 해당 bit를 끄기 위해서는 AND연산을 이용해야 한다.
1<<k는 k번째 bit만 켜진 상태이며, 여기에 NOT을 씌우면 k번째 bit만 꺼진 상태가 된다.
그러므로 AND 연산을 적용하면 k번째 bit만 0이 되고 나머지 bit는 변함이 없다.
④ 원소의 포함 여부 확인
A 집합에 특정 원소가 포함되어 있는지 확인하는 방법이다. k번째 원소가 포함되어 있는지 확인하고 싶다면, k번째 bit가 켜져 있는지(1)만 확인하면 된다.
⑤ 원소의 토글
A 집합에 해당 원소가 빠져있는 경우에는 추가하고, 들어있는 경우에는 삭제하는 방법이다. XOR 연산을 이용한다.
⑥ 두 집합의 연산
두 집합을 A와 B라고 한다면 비트연산자들을 통해서 A와 B의 교집합, 합집합, 차집합 등을 구할 수 있다.
⑦ 집합의 크기 구하기
비트가 1인 비트의 수를 count 한다. 따라서, 모든 비트를 순회하고 재귀적으로 구현할 수 있다.
x % 2는 마지막 비트를 얻게 되고, x / 2는 마지막 비트를 삭제할 수 있다. 그러므로 모든 비트 재귀적으로 순회가 가능하다.
⑧ 최소 원소 찾기
집합에 포함된 가장 작은 원소 (index가 가장 작은 원소)를 찾는 방법이다. 켜져 있는 bit 중에서 가장 오른쪽에 있는 bit를 찾는 것이다.
컴퓨터는 2의 보수를 이용하여 음수를 표현하기 때문에 -A를 표현하기 위해서 ~A + 1을 이용한다.
A에서 가장 오른쪽에 켜진 bit의 인덱스를 k라고 한다면, k보다 오른쪽에 있는 모든 bit는 0이다.
따라서 NOT 연산을 적용한 ~A는 k번째 bit는 0이고, 오른쪽의 모든 bit는 1이 된다.
여기서 ~A에 1을 더해주게 되면 k번째보다 오른쪽에 있는 bit는 모두 0이 되고, k번째 bit는 1이 된다. k번째 bit보다 왼쪽에 있는 bit는 아무런 변화가 없다.
따라서 -A와 A를 AND 시키면 k번째 bit만 켜진 상태로 남게 된다.
⑨ 최소 원소 지우기
가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND시키면 된다. A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.
