Upper bound, Lower bound 알고리즘에 대하여 이해해보자.
이진 탐색 알고리즘은 정렬된 배열에서 특정한 값의 위치를 찾는 알고리즘이다.
Upper bound, Lower bound 알고리즘은 이진 탐색에서 파생된 것으로, 이진탐색과 마찬가지로 배열 안의 숫자들이 정렬되어 있을 때 이용할 수 있다.
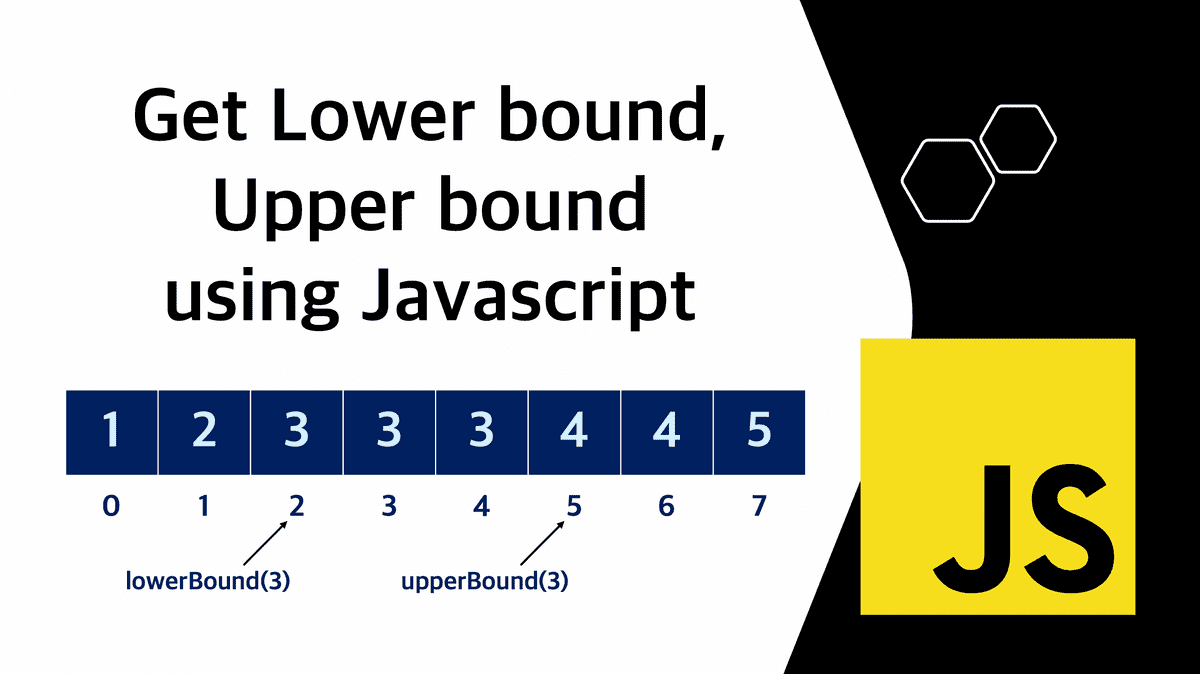
k(임의의 수)의 Lower bound는 배열에서 원하는 값 k 이상의 수가 처음으로 나오는 위치이고, k(임의의 수)의 Upper bound는 k를 초과하는 수가 처음으로 나오는 위치이다.

Lower bound
-
Lower bound알고리즘은 원하는 값 k 이상의 수가 처음으로 나오는 위치를 찾는다. 파악하고자 하는 구간의 시작 위치를 start, 끝 위치를 end라고 할 때, 구간의 시작 위치가 끝 위치보다 뒤에 오기 전까지 다음 과정을 반복한다. -
중간 지점 mid 위치의 값이 k보다 작을 때
mid가 lower bound가 될 수 없으므로, 더 큰 값을 찾기 위해 뒷 구간 [mid+1, end]에 대해 이 과정을 반복한다. -
그 외의 경우
mid가 lower bound 값이 될 수 있으므로, 결과 변수에 기존 값과 mid를 비교해 더 작은 값을 저장하고, lower bound가 될 수 있는 더 작은 값이 있는지 파악하기 위해 앞 구간 [start, mid-1]에 대해 이 과정을 반복한다.
const arr = [1, 2, 3, 3, 3, 4, 4, 6, 8, 9];
// 중복된 값이 있더라도 그 값중에서 맨 앞의 위치를 반환한다.
console.log(lowerBound(arr, 3));
// 찾고자 하는 값이 존재하지 않더라도 5이상의 값의 위치를 반환한다.
console.log(lowerBound(arr, 5));
function lowerBound(arr, data) {
let result = Number.MAX_SAFE_INTEGER;
let start = 0;
let end = arr.length - 1;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
if (arr[mid] < data) {
start = mid + 1;
continue;
}
result = Math.min(result, mid);
end = mid - 1;
}
return result;
}Upper bound
-
Upper bound알고리즘은 원하는 값 k를 초과하는 수가 처음으로 나오는 위치를 찾는다. 파악하고자 하는 구간의 시작 위치를 start, 끝 위치를 end라고 할 때, 구간의 시작 위치가 끝 위치보다 뒤에 오기 전까지 다음 과정을 반복한다. -
중간 지점 mid 위치의 값이 k 이하일 때
mid가 upper bound가 될 수 없으므로, 더 큰 값을 찾기 위해 뒷 구간 [mid+1, end]에 대해 이 과정을 반복한다. -
그 외의 경우
mid가 lower bound 값이 될 수 있으므로, 결과 변수에 기존 값과 mid를 비교해 더 작은 값을 저장하고, upper bound가 될 수 있는 더 작은 값이 있는지 파악하기 위해 앞 구간 [start, mid-1]에 대해 이 과정을 반복한다.
const arr = [1, 2, 3, 3, 3, 4, 4, 6, 8, 9];
// 중복된 값이 있더라도 그 값중에서 맨 앞의 위치를 반환한다.
console.log(lowerBound(arr, 3));
// 찾고자 하는 값이 존재하지 않더라도 5초과의 값의 위치를 반환한다.
console.log(lowerBound(arr, 5));
function lowerBound(arr, data) {
let result = Number.MAX_SAFE_INTEGER;
let start = 0;
let end = arr.length - 1;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
// lowerBound는 arr[mid] < data이다.
if (arr[mid] <= data) {
start = mid + 1;
continue;
}
result = Math.min(result, mid);
end = mid - 1;
}
return result;
}TIL
새롭게 배운 것
- 이분 탐색 알고리즘에서 파생된 Lower Bound, Upper Bound 알고리즘
- 이분 탐색 알고리즘과 Lower Bound, Upper Bound 알고리즘의 차이
이분 탐색이 '원하는 값 k를 찾는 과정' 이라면 Lower Bound는 '원하는 값 k 이상이 처음 나오는 위치를 찾는 과정' 이며, Upper Bound는 '원하는 값 k를 초과한 값이 처음 나오는 위치를 찾는 과정'이다.
깨달은 점
-
이분 탐색 알고리즘에서의 존재하지 않는 값에 대한 처리를 Lower Bound, Upper Bound 알고리즘을 활용하여 다양한 상황에서의 예외 처리가 가능해지는 점에서 활용도를 더 높일 수 있었다.
-
이분 탐색 알고리즘의 중복된 값의 요소들이 존재할 때의 값의 위치의 하한을 정함으로써 좀 더 명확해지는 값의 경계에 대해 Lower Bound 알고리즘의 사용도를 좀 더 이해할 수 있었다.
-
이분 탐색에서의 값의 하한과 상한을 통한 데이터 탐색법에 대한 이해도를 더 높일 수 있었다.
