투 포인터, 슬라이딩 윈도우, 구간 합 알고리즘

MyeonghoonNam·2021년 9월 30일

알고리즘

목록 보기

17/22

투 포인터와 슬라이딩 윈도우 알고리즘은 선형 공간(1차원 배열)을 2회 이상 반복적으로 탐색해야 할 경우 O(N^2) 이상 걸릴 시간 복잡도를 부분 배열을 활용하여 O(N)으로 줄일 수 있다는 공통점이 있습니다.

그렇다면 이 두 알고리즘의 차이점은 무엇일까요 ?

바로, 부분 배열 길이의 변화 여부입니다.

더 쉽게 말해서, 투 포인터 알고리즘은 부분 배열의 길이가 가변적이지만 슬리이딩 윈도우 알고리즘은 부분 배열의 길이가 고정적입니다.

투 포인터

투 포인터는 연속되고 길이가 가변적인 부분 배열들을 활용하여 특정 조건을 일치시키는 알고리즘입니다.

여기서 중요한 것은 "연속되고 가변적인"입니다. 값이 연속된다는 말은 정렬을 뜻하는 것일 수도 있으니 부분 배열로 작성하였습니다. 만약 문제에서 주어진 배열이 연속된 부분 배열을 통하여 문제를 해결하라는 것이 아니면 (예를 들어, 연속적이지 않은 arr[0]과 arr[3]을 부분 배열로 하는 문제) 투 포인터 알고리즘을 사용할 수 없습니다.

이런 상황에서는 주어진 배열을 그대로 이용하여 문제를 해결하거나 배열의 인덱스와 값을 함께 list에 저장한 후 오름차순, 혹은 내림차순 정렬을 통하여 연속성을 추가해준 다음에 투 포인터 알고리즘을 사용하여야 합니다.

즉, 투 포인터 알고리즘에서는 대게 두 개의 유형이 존재합니다.

1) 2개의 포인터 변수 시작점이 배열의 시작점인 경우

2) 정렬된 배열 안에서 2개의 포인터 변수가 각각 시작점과 끝점(arr.length-1)에 위치한 경우

만약, 정수로 이루어진 배열에서 연속된 부분 배열의 합이 특정 값(Target)을 이루는 부분 배열의 개수를 구하는 문제가 있다고 가정했을 때, 두 포인터 변수의 이동 조건은 다음과 같습니다.

(1) 부분 배열의 합이 Target 값보다 크거나 같으면 Left = Left + 1 해줍니다. (부분 배열의 길이를 줄여 합을 빼준다. )

if(sum >= Target) Left++;

(2) 부분 배열의 합이 Target 값보다 작으면 Right = Right + 1 해줍니다. (부분 배열의 길이를 늘려 합을 더한다.)

if(sum < Target) Right++;

(3) 부분 배열의 합이 Target 값과 같다면 결과 값을 +1 해줍니다.

if( sum == Target) count++;

(1)에서 부분 배열의 합이 Target과 같은데 왜 Left를 늘려주냐 라는 의문이 생길 수도 있습니다. 이건 아주 간단합니다. 다음 배열을 탐색해야 하기 때문에 left를 늘려주는 것입니다.

구현

아래와 같이 자연수로 구성된 수열에서 합이 5인 부분 연속 수열의 개수를 구해보자.

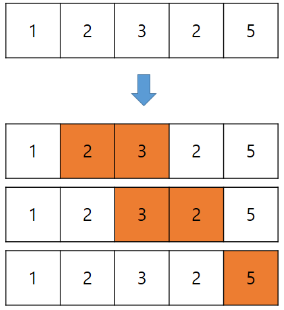
위 그림과 같이 연속된 배열의 합이 5가 되는 부분 수열의 수를 찾으면 된다.

이중 반복문을 이용한 완전 탐색으로 문제를 해결할 수 도 있지만 그럴경우 O(N^2)의 시간 복잡도가 발생하게 되며 그 보다 적은 시간복잡도를 통해 문제를 해결해야 하는 경우라면 투 포인터 알고리즘을 활용하여 O(N)의 시간복잡도로 문제를 해결할 수 있다.

function solution(n, arr) {
	let result = 0; // 부분 수열의 요소의 전체 합이 n인 부분 수열의 개수
  let sum = 0; // 부분 수열의 요소 전체 합
  let end = 0; // 투 포인터에서 끝 점에 해당된다.

  // 시작점 start를 배열 시작부터 오른쪽으로 한 칸씩 옮긴다.
  for(let start = 0; start < arr.length; start++) {
    // 끝점 end를 가능한 만큼 이동
    while(sum < n && end < arr.length) {
      sum += arr[end];

      end++;
    }

    if(sum === n) {
      result++;
    }

    sum -= arr[start];
  }

  return result;
}

const arr = [1, 2, 3, 2, 5];
console.log(solution(5, arr))

슬라이딩 윈도우

슬라이딩 윈도우 알고리즘은 연속되는 투 포인터와 유사하게 부분 배열들을 활용하여 특정 조건을 일치시키는 알고리즘이지만 부분 배열의 길이(크기)가 고정적입니다. 어떤 창문을 왼쪽부터 오른쪽으로 밀어 오면서 창문 안에 있는 값들을 부분 배열이라고 생각하면 될 것 같습니다.

또 다른 차이점은 투 포인터 알고리즘은 부분 배열의 길이가 가변적이기 때문에 부분 배열의 구간을 정할 2개의 포인터 변수가 필요한 반면, 슬라이딩 윈도우 알고리즘은 부분 배열의 길이를 고정적으로 잡기 때문에 포인터 변수가 2개일 필요가 없습니다. 즉, 고정적인 부분 배열의 크기를 나타내는 변수가 있다면 포인터 하나만 있어도 부분 배열의 크기를 알고 있기 때문에 각 배열의 끝을 어딘지 알 수 있습니다.

슬라이딩 윈도우 알고리즘을 구현하는 방법도 간단합니다. 아래 주황색 칸이 3의 고정 길이를 가지는 부분 배열이라 가정하겠습니다. 주어진 문제가 부분 배열의 합을 구하는 것이라 할 때, 오른쪽으로 한 칸 옮기더라도 옮기기 전 부분 배열과 옮기고 난 후에는 겹치는 부분이 존재합니다. 즉, 기존 구간에서 빠지게 되는 가장 왼쪽 칸의 값은 삭제하고 새 구간에 포함되는 값을 추가해주면 됩니다.

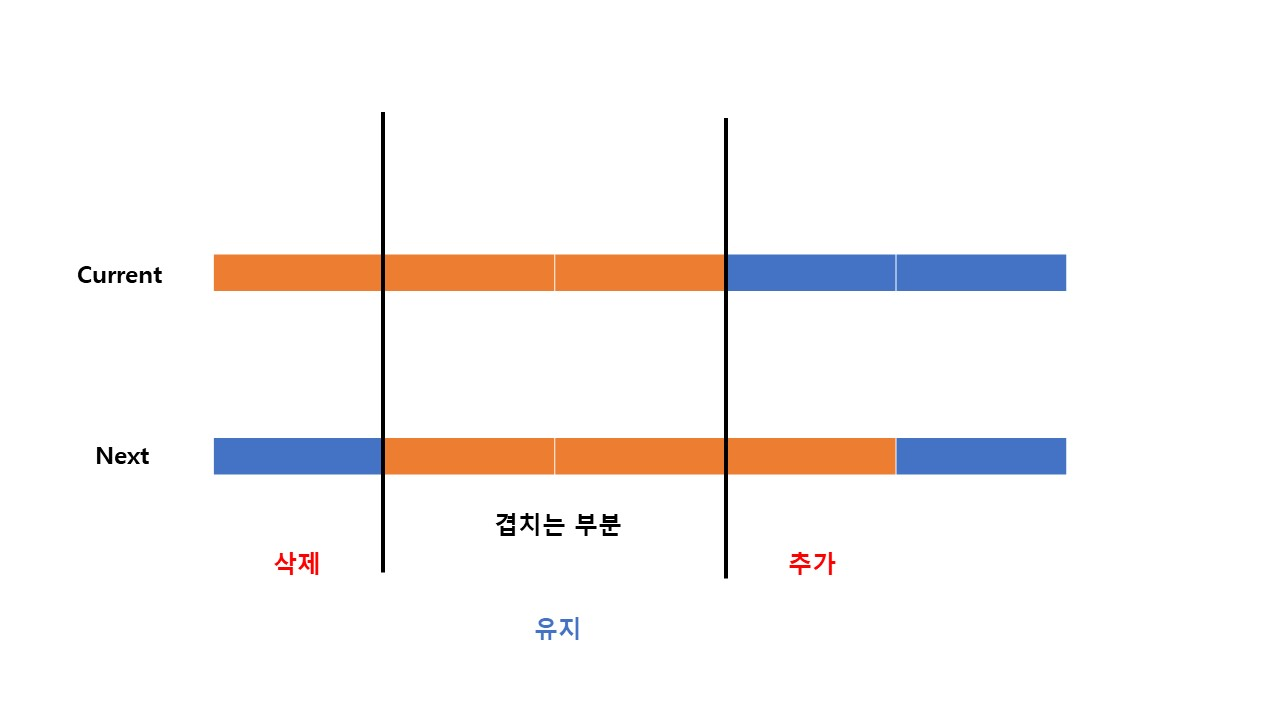
구현

문제

현수의 아빠는 제과점을 운영합니다. 현수 아빠는 현수에게 N일 동안의 매출기록을 주고 연속 된 K일 동안의 최대 매출액이 얼마인지 구하라고 했습니다.
만약 N=10이고 10일 간의 매출기록이 아래와 같습니다. 이때 K=3이면
12 15 11 20 25 10 20 19 13 15
연속된 3일간의 최대 매출액은 11+20+25=56만원입니다. 여러분이 현수를 도와주세요.
[입력설명]
첫 줄에 N(5<=N<=100,000)과 M(2<=K<=N)가 주어집니다.
두 번째 줄에 N개의 숫자열이 주어집니다. 각 숫자는 500이하의 음이 아닌 정수입니다.
[출력설명]
첫 줄에 최대 매출액을 출력합니다.

입력 예제

10 3
12 15 11 20 25 10 20 19 13 15

출력 예제

function solution(n, k, arr) {
  let result = 0; // 길이 k의 부분 수열의 요소 전체 합의 최댓값
  let sum = 0; // 특정 부분 수열의 전체 합

  for(let i = 0; i < k; i++) {
    sum += arr[i];
  }

  result = sum;

  for(let i = k; i < arr.length; i++) {
    sum += (arr[i] - arr[i - k]);
    result = Math.max(result, sum);
  }

  return result;
}

const n = 10;
const k = 3;
const arr = [12, 15, 11, 20, 25, 10, 20, 19, 13, 15];

console.log(solution(n, k, arr));

구간 합(Prefix Sum)

위의 두 알고리즘과 비슷하게 배열의 특정 연속된 구간에 대한 처리를 목적으로 하는 알고리즘입니다.

차이를 비교해보자면 위의 두 알고리즘은 0~특정길이의 구간에 대한 처리를 한다면 구간 합은 특정위치 a,b가 주어졌을 때 배열에서 a~b의 구간에 대한 처리를 다룬다고 할 수 있습니다.

구현

배열의 앞에서부터 특정 위치까지의 합인 접두사 합을 활용하는 방식을 사용

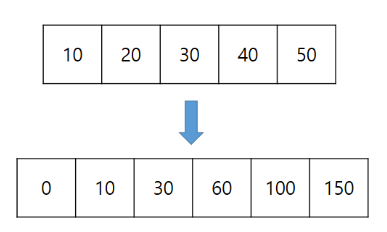
function solution(l, r, arr) {
  let sum = 0;
  const prefixSum = [0];

  for(let i = 0; i < arr.length; i++) {
    sum += arr[i];
    prefixSum.push(sum);
  }

  return prefixSum[r] - prefixSum[l - 1]; // 특정 구간의 합
}

const arr = [10, 20, 30, 40, 50];
console.log(solution(2, 5, arr)); // 2~5의 구간