📌 정규화(normalization)

이상 현상이 발생하는 테이블을 수정하여 정상으로 만드는 과정을 정규화(normalization)라고 한다.
정규화를 하기 위해서는 우선 테이블을 분석하여 기본키와 함수 종속성을 파악해야 한다.
그 후 릴레이션을 분해하여 제거한다.
분해된 릴레이션에 이상현상이 남아 있다면 없어질 때까지 분해 한다.

TIP
릴레이션과 테이블은 같은 의미로 쓰인다.
보통 테이블은 실무와 같은 구조보다 데이터를 강조하는 측면이 있고
릴레이션은 구조에 관한 이론을 강조하는 텍스트측면이 있다.

❓ 이상현상(anomaly)?

이상이란 잘못 설계된 테이블로 삽입, 수정, 삭제와 같은 데이터 조작시 일어나는 일이다.
ex) 튜플 삽입시 NULL 삽입, 하나의 튜플 삭제시 연쇄 삭제, 수정시 불일치 문제 발생 등

❓ 함수 종속성(FD, Functional Dependency)?

수강 신청 릴레이션

![https://velog.velcdn.com/images%2Fcoding_egg%2Fpost%2F43077776-3848-4fa4-9cee-1316f4f6d6ca%2F%EA%B7%B8%EB%A6%BC1.png%5D(https%3A%2F%2Fimages.velog.io%2Fimages%2Fcoding_egg%2Fpost%2F43077776-3848-4fa4-9cee-1316f4f6d6ca%2F%EA%B7%B8%EB%A6%BC1.png)

수강 신청 릴레이션은 각 속성 사이에 의존성이 존재한다.
'알고리즘' 강좌는 '계란관 101' 한 곳 뿐이다.
반면 이름이 '유정란'인 경우에는 '알고리즘', '데이터베이스' 두 강좌가 있다.

이처럼 강좌이름을 알면 강의실을 알 수 있는데
어떤 속성 A를 알면 B의 값이 유일해지는 의존 관계를 '속성B는 속성A에 종속한다' or '속성A는 속성B를 결정한다'라고 한다.
그리고 A → B와 같이 표기 한다.

A → B와 같이 왼쪽 속성(A)의 모든 값에 의하여 오른쪽 속성(B)의 값이 유일하게 결정될때 '함수적으로 종속한다'라고 한다. 그리고 이렇게 종속하는 성질을 함수 종속성이라고 한다.

함수 종속성 규칙

부분집합 규칙: if Y ⊆ X, then X → Y
증가 규칙: if X → Y, then XZ → YZ
이행 규칙: if X → Y and Y → Z, then X → Z

위의 세 가지 규칙으로 얻을 수 있는 규칙
결합 규칙: if X → Y and X → Z, then X → YZ
분해 규칙: if X → YZ, then X → Y and X → Z
유사 이행 규칙: if X → Y and WY → Z, then WX → Z

이 함수 종속성의 규칙은 릴레이션에 적용된다.

🔍 이상현상과 결정자

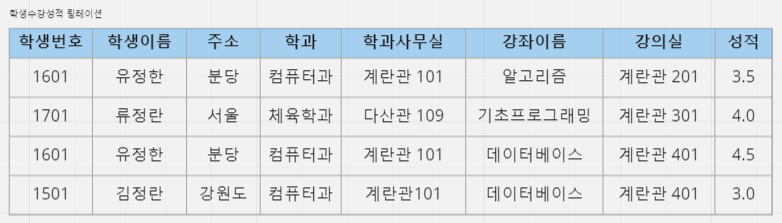
이상현상은 한개의 릴레이션에 두개 이상의 정보가 포함되어 있을때 나타난다.
학생수강성적 릴레이션의 경우 학생정보와 강좌정보가 한 릴레이션에 포함되어 있기 때문에 이상현상이 나타난다.

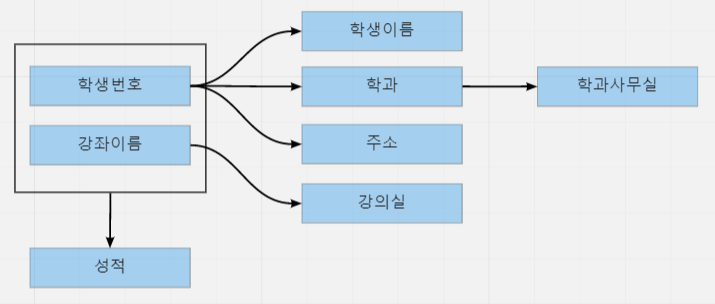
모든 결정자를 살펴보면 (학생번호, 강좌이름), 학생번호, 강좌이름, 학과 이다.
이 중 (학생번호, 강좌이름)은 키본키이면서 결정자이고 학생번호, 강좌이름, 학과는 키본키가 아니면서 결정자이다.
이상현상은 기본키가 아니면서 결정자인 속성이 있을때 발생함으로 릴레이션을 분해해야한다.

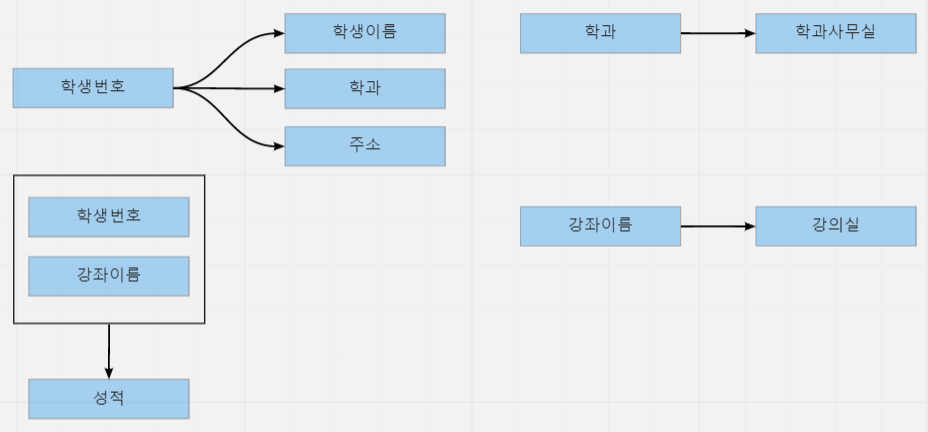
위의 사진과 분해할 경우 더 이상 이상현상이 발생하지 않는다.

🔍 정규화 과정

이상현상이 발생하는 릴레이션을 분해하여 이상현상을 없애는 과정을 정규화라고 한다.
릴레이션은 정규형이라는 개념으로 구분하며 정규형이 높을수록 이상현상은 줄어든다.

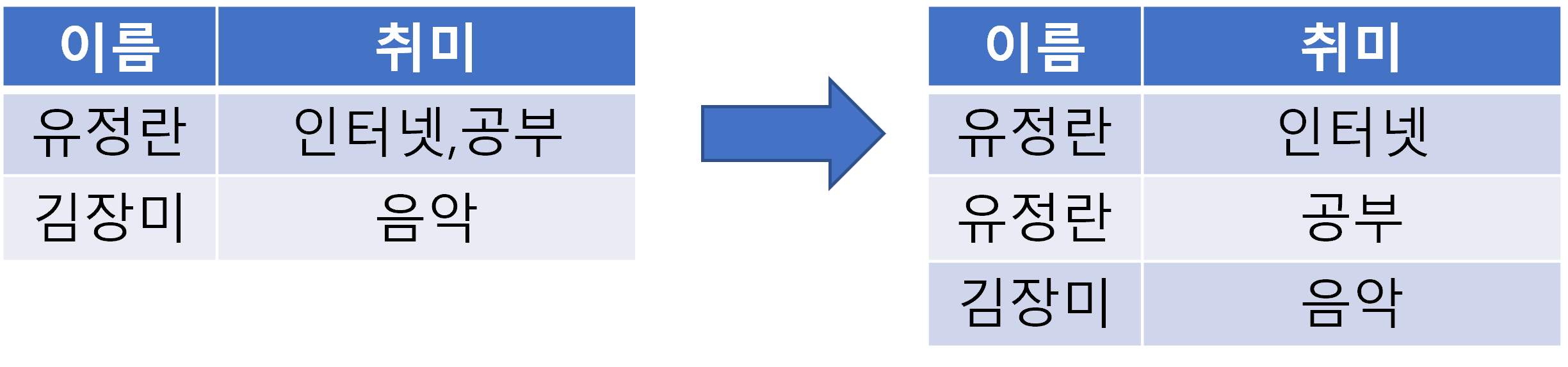
제 1정규형

정의: 릴레이션 R의 모든 속성 값이 원자값을 가지면 제 1정규형이다.

예시

제 2정규형

제 2정규형은 릴레이션의 기본키가 복합키일 때, 복합키의 일부분이 다른 속성의 결정자인지 여부를 판단하는 것이다.
정의: 릴레이션 R이 제 1정규형이고 기본키가 아닌 속성이 기본키에 완전 함수 종속일때 제 2정규형이라고 한다.

완전 함수 종속성

제 2정규형을 이해하기 위해서는 완전 함수 종속성을 알아야 한다. 정의는 다음과 같다
정의: A와 B가 릴레이션R의 속성이고 A → B 종속성이 성립할때, B가 A의 속성 전체에 함수 종속하고 부분 집합 속성에 함수 종속하지 않을 경우 완전 함수 종속(full functional dependency)이라고 한다.

ex) (A1, A2) → B인데 A1 → B 이면 불완전 함수 종속이다.

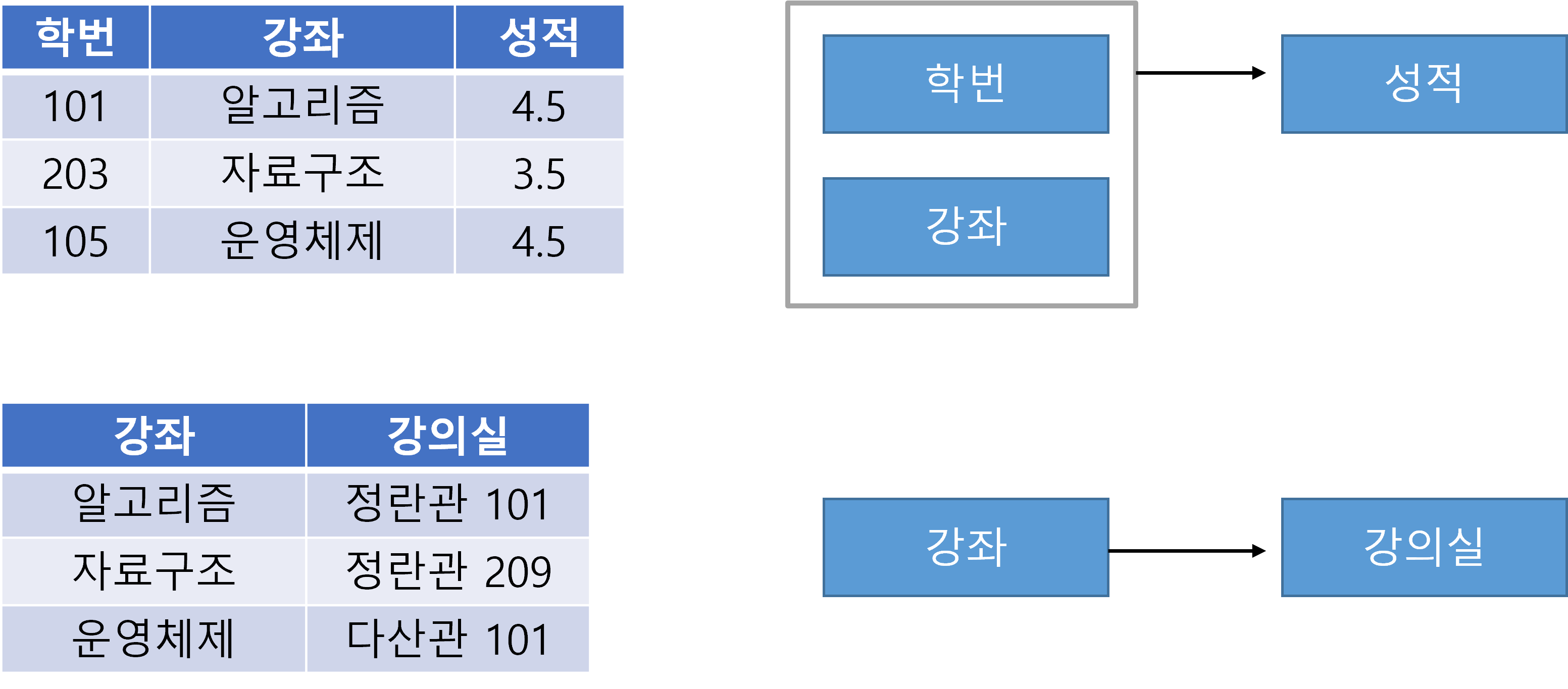
예시

이상현상

• 삭제이상
  101 학번의 학생이 수강을 취소하게 되면 알고리즘 과목의 강의실에 대한 정보가 사라진다.
• 삽입이상
  '세계사'라는 과목이 '정란관102'로 새로 개설되어도 신청한 학생이 없어 학번과 성적에 NULL값을 넣어야 한다.

2정규형으로 변환

제 3정규형

제 3정규형은 속성들이 이행적으로 종속되어 있는지 여부를 판단하는 것이다.
정의: 릴레이션R이 제 2정규형이고 기본키가 아닌 속성이 기본키에 비이행적으로 종속할 때 제 3정규형이라고 한다.
TIP 이행적 종속이란 A → B, B → C가 성립할 때 A → C가 성립되는 함수 종속성이다.

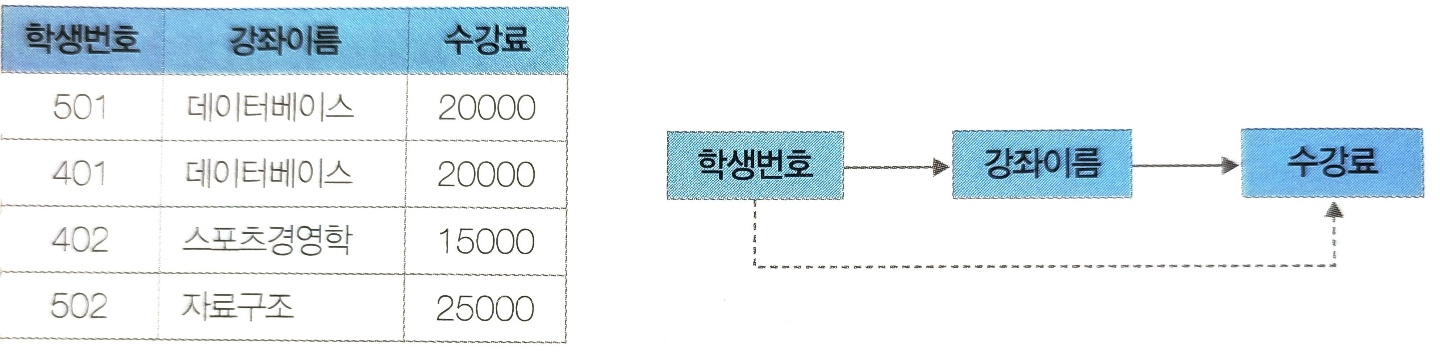
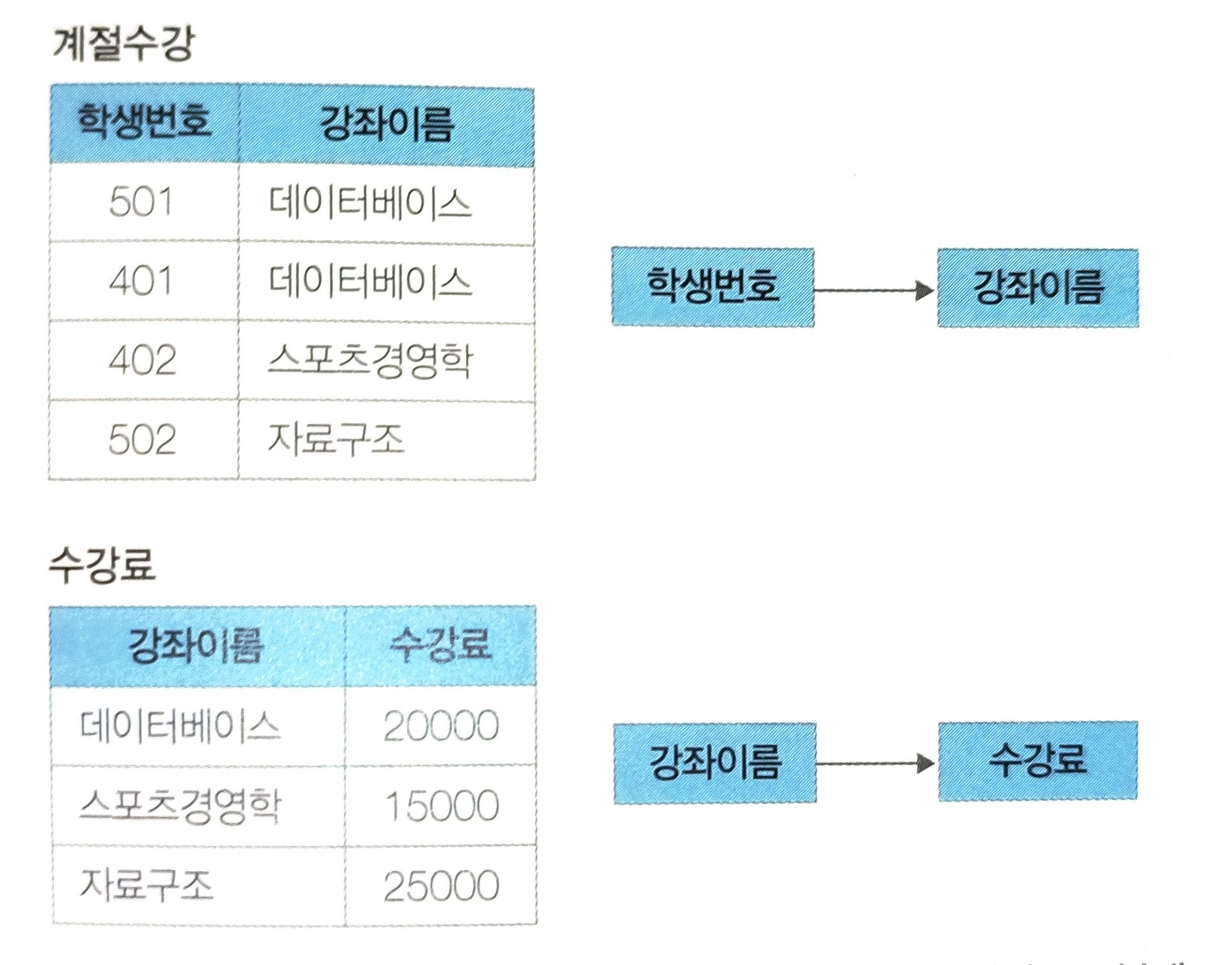
예시

이상현상

• 삭제이상
  402 학번의 학생이 수강을 취소하게 되면 스포츠경영학 과목의 수강료에 대한 정보가 사라진다.
• 삽입이상
  운영체제 과목이 개설되어 15,000원을 삽입 해야 하는데, 아직 신청한 학생이 없어 학번을 NULL값으로 삽입해야하는 문제 발생
• 수정이상
  데이터베이스 수강료를 15,000원으로 변경할 경우 데이터 불일치가 발생할 가능성이 있다.

제 3정규형으로 변환

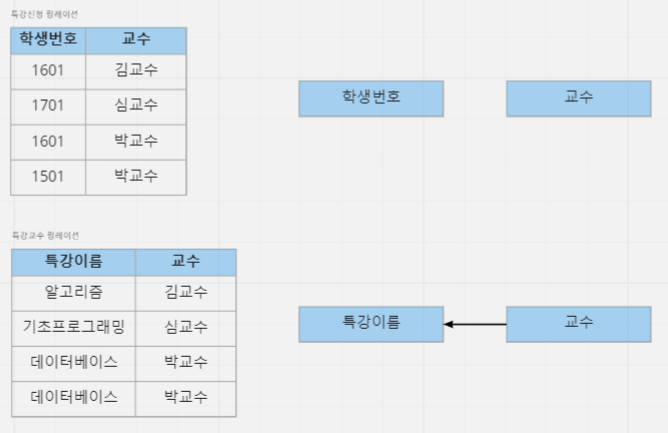
BCNF

릴레이션에 존재하는 함수 종속성에서 모든 결정자가 후보키이면 BCNF(Boyce Codd Normal Form) 정규형이다.
정의: 릴레이션 R에서 함수 종속성 X → Y가 성립할 때 모든 결정자 X가 후보키이면 BCNF 정규형이라고 한다.

TIP 후보키는 기본키로 사용할 수 있는 속성들을 뜻한다.
즉 유일성과 최소성을 만족해야 한다.

예시

이상현상

• 삭제이상
  1601번의 학생이 수강을 취소하면 김교수의 정보가 사라진다.
• 삽입이상
  최교스기 특강을 새로 열면 아직 신청한 학생이 없어 학생번호를 NULL 값으로 삽입해야 한다.
• 수정이상
  박교수가 특강이름을 데이터베이스 개론으로 변경할 경우 불일치가 발생할 수 있다.

이상현상의 원인

교수는 특강이름을 결정하는 결정자이면서 후보키가 아니다.
이와 같이 결정자이면서 후보키가 아닌 속성이 존재하면 이상현상이 발생한다.

BCNF정규형으로 변환

🎉 정리

제 4정규형은 다치종속성을 가진 릴레이션에 관한 내용, 제 5정규형은 프로젝트-조인 정규형이라고 부르며 조인종석성을 가진 릴레이션이다. 대부분의 릴레이션은 BCNF까지 정규화하면 실제적인 이상현상은 없어진다. 그래서 이 글에서도 따로 다루지는 않는다.

✨ References

• 박우창, 남송휘, 이현룡, 『mysql로 배우는 데이터베이스 개론과 실습』, 한빛아카데미