BAEKJOON : 10844, 2193

No. 10844

1. Problem

2. My Solution

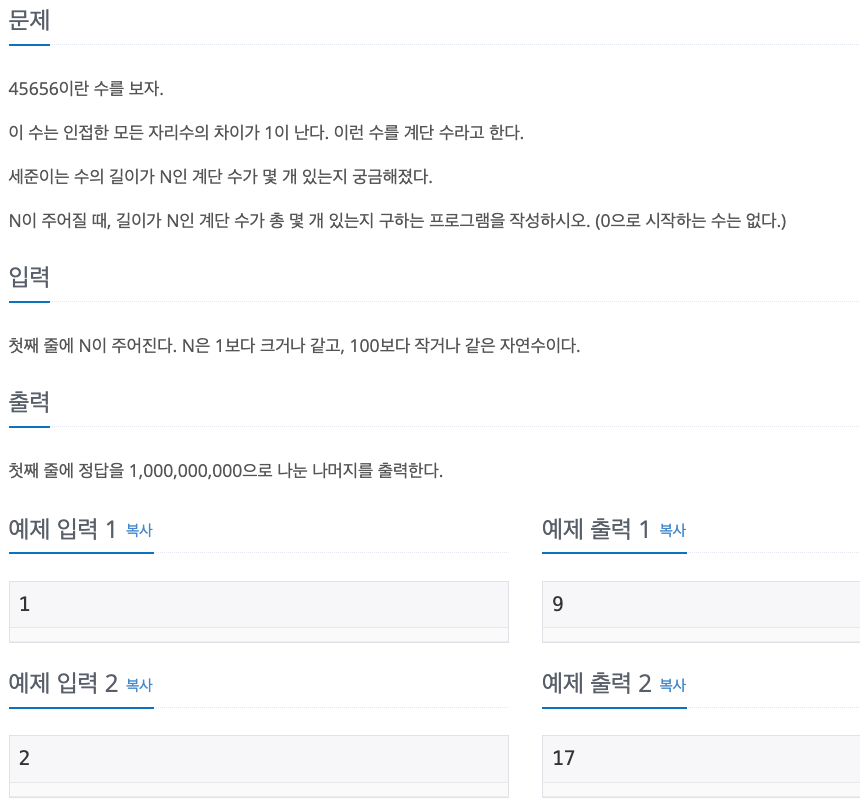
• 길이가 n 인 계단 수는 10가지 경우로 나뉨
  - 끝이 0으로 끝나는 수
  - 끝이 1로 끝나는 수
  - 끝이 2로 끝나는 수
  - ...
  - 끝이 9로 끝나는 수

• 끝이 어떤 수로 끝나는지에 대한 정보까지 저장하기 위해 이차원 배열 이용
• 인접한 수의 차이가 1이어야 하므로 맨 끝에 1 큰수 또는 1 작은 수가 추가될 수 있음
• 예) 길이가 n인 계단 수에서 1로 끝나는 수의 개수는 n-1 에서 0 또는 2로 끝나는 수의 개수를 더한 값
• 단, 예외로 0은 1,  9는 8만 올 수 있으므로 따로 처리가 필요함

import sys

n = int(sys.stdin.readline().rstrip())

dp = [[0]*10 for _ in range(101)]
dp[1] = [0,1,1,1,1,1,1,1,1,1]

for i in range(2,n+1):
   for j in range(0,10):
        if j == 0:
            dp[i][j] = dp[i-1][j+1] % 1000000000
        elif j == 9:
            dp[i][j] = dp[i-1][j-1] % 1000000000
        else:
            dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % 1000000000

print(sum(dp[n]) % 1000000000)

---

No. 2193

1. Problem

2. My Solution

• 첫 번째 방법
• n = 1 부터 규칙을 찾음 -> 피보나치수의 원리

import sys

n = int(sys.stdin.readline().rstrip())
dp = [0]*91
dp[1] = dp[2] = 1

for i in range(2,n+1):
    dp[i] = dp[i-1] + dp[i-2]

print(dp[n])

• 두 번째 방법
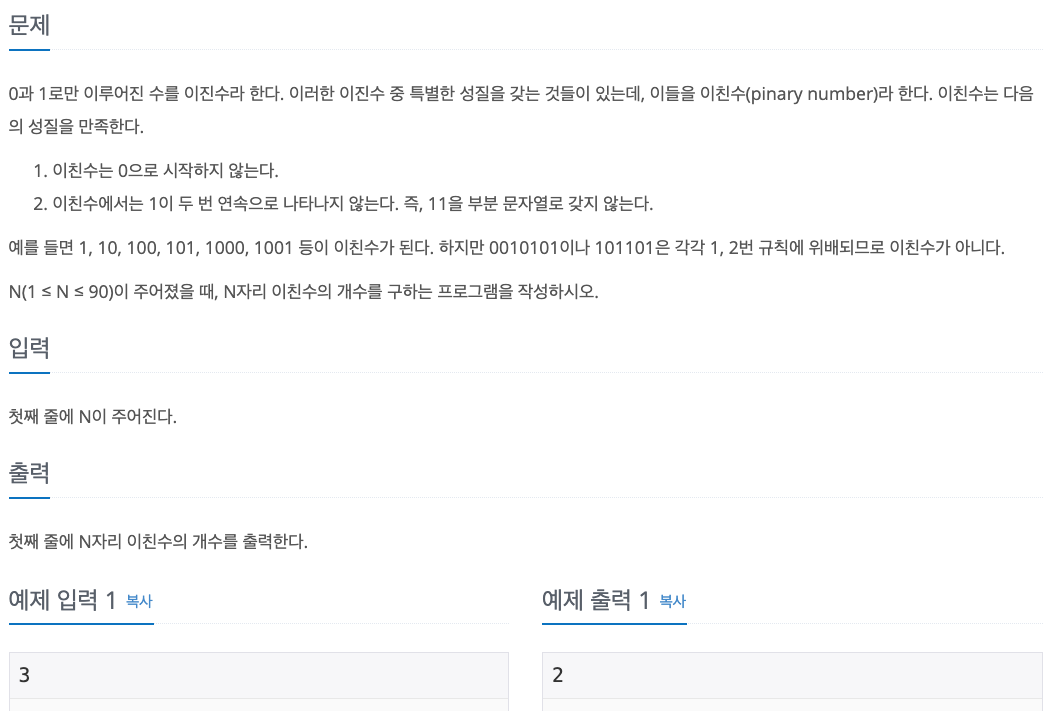
• n 자리 이친수는 2가지 경우로 나뉨
  - 끝이 0으로 끝나는 이친수
  - 끝이 1로 끝나는 이친수

• 끝이 어떤 수로 끝나는지에 대한 정보까지 저장하기 위해 이차원 배열 이용
• 끝이 0으로 끝나면 0과 1이 추가될 수 있음, 1로 끝나면 0만 가능

import sys

n = int(sys.stdin.readline().rstrip())
dp = [[0,0] for _ in range(91)]
dp[1][1] = 1

for i in range(2,n+1):
    dp[i][0] = dp[i-1][0] + dp[i-1][1]
    dp[i][1] = dp[i-1][0]

print(sum(dp[n]))

4. Learned

• 여러 가지 방법으로 알고리즘을 구현해보자