BAEKJOON : 1149, 1309, 11057

No. 1149

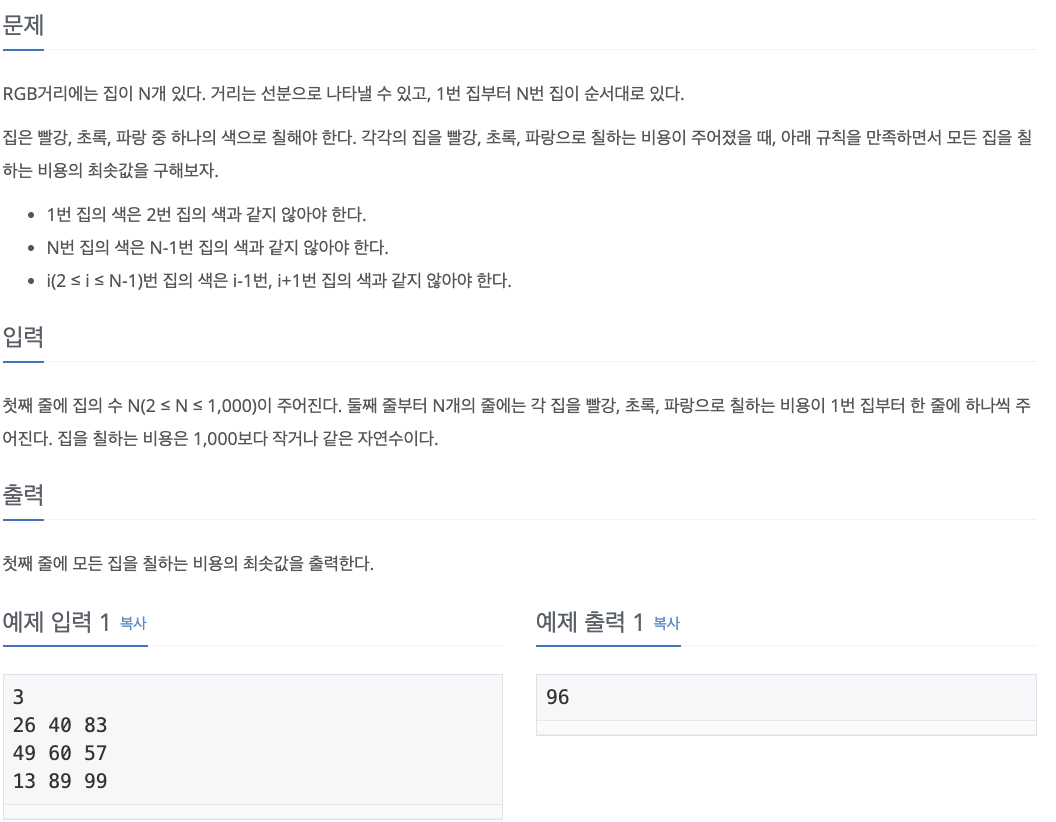
1. Problem

2. My Solution

• i 는 몇 번째 집인지 나타내고, j 는 집의 색으로 하는 dp[i][j] 생성 (R = 0, G = 1, B = 2)
• i 번째 집을 RGB 각각 칠할 때 최소의 비용 값을 모두 저장
• 만약 i 번째 집을 R(0)로 칠할 때는 i-1 번째 집이 G(1) 또는 B(2)로 칠해진 경우에만 가능

# dp[i][j] -> i = n, j = color (R = 0, G = 1, B = 2)

import sys

n = int(sys.stdin.readline().rstrip())
dp = [[0,0,0] for _ in range(n+1)]
color_cost =[[0,0,0]]

for _ in range(n):
    color_cost.append(list(map(int,sys.stdin.readline().rstrip().split())))

for i in range(3):
    dp[1][i] = color_cost[1][i]

for i in range(1,n+1):
    dp[i][0] = min(dp[i-1][1]+color_cost[i][0],dp[i-1][2]+color_cost[i][0])
    dp[i][1] = min(dp[i-1][0]+color_cost[i][1],dp[i-1][2]+color_cost[i][1])
    dp[i][2] = min(dp[i-1][0]+color_cost[i][2],dp[i-1][1]+color_cost[i][2])

print(min(dp[n]))

---

No. 1309

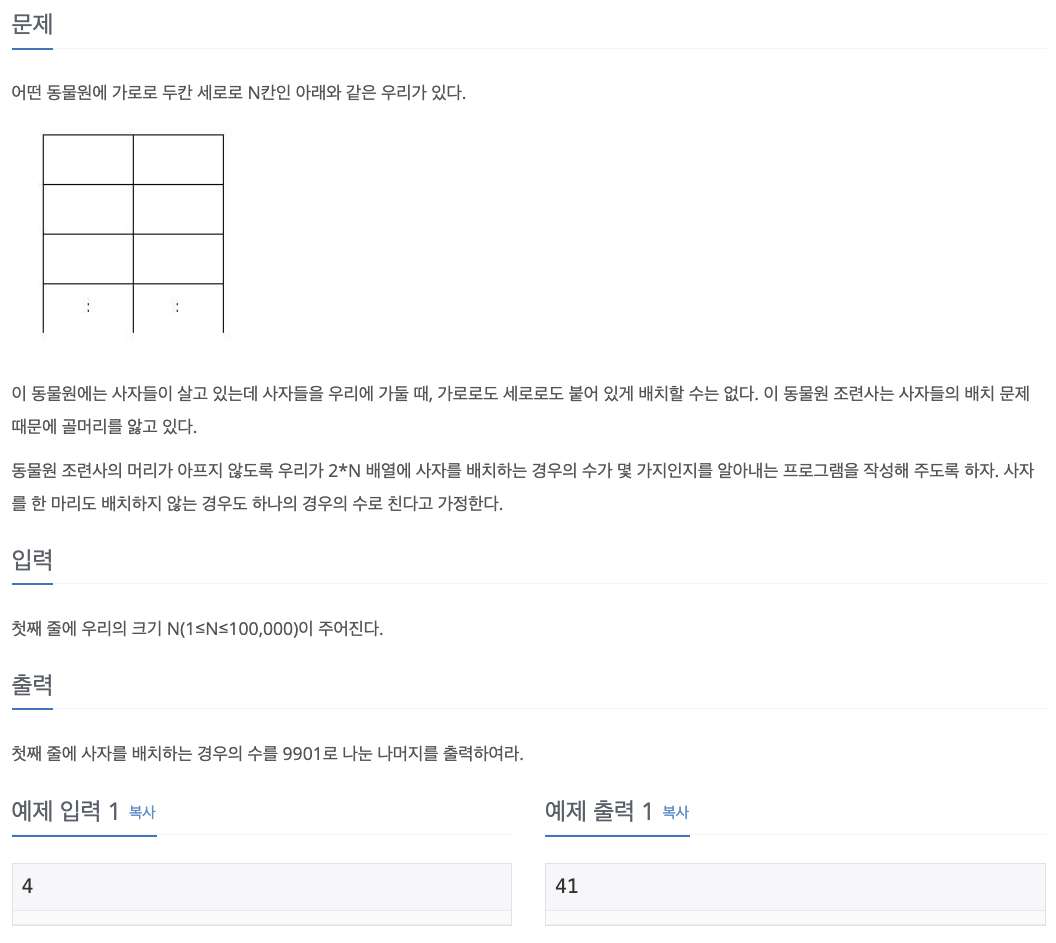
1. Problem

2. Others' Solutions

• n이 증가할 때 사자가 없는 경우, 왼쪽에 있는 경우, 오른쪽에 있는 경우로 나눔

# dp[i][j] -> i = n, j = 사자의 위치 (0 = 없음, 1 = 왼쪽, 2 = 오른쪽)

import sys

n = int(sys.stdin.readline().rstrip())
dp = [[0,0,0] for _ in range(100001)]

for i in range(3):
    dp[1][i] = 1

for i in range(2,100001):
    dp[i][0] = (dp[i-1][0] + dp[i-1][1] + dp[i-1][2]) % 9901
    dp[i][1] = (dp[i-1][0] + dp[i-1][2]) % 9901
    dp[i][2] = (dp[i-1][0] + dp[i-1][1]) % 9901

print(sum(dp[n]) % 9901)

3. Learned

• dp 에서 n이 증가할 때 어떤 경우로 나누어지는지 생각해보자

---

No. 11057

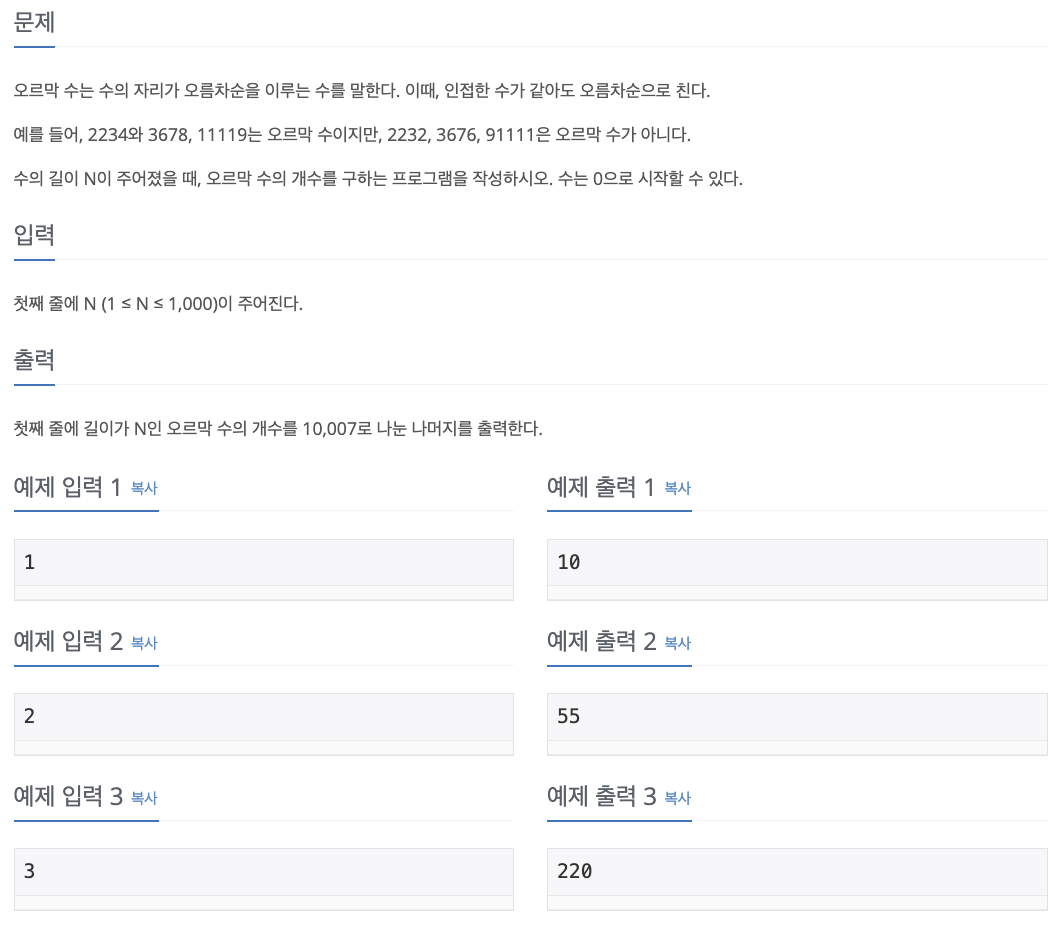
1. Problem

2. My Solution

• 오르막수는 0으로 끝나는 경우, 1로 끝나는경우.....9로 끝나는 경우로 나뉨
• i 는 오르막수의 길이, j 는 어떤 수로 끝나는지에 대한 정보를 담는 dp[i][j]
• j 로 끝나는 오르막수는 i-1 길이의 오르막수에서 j 보다 작거나 같은 수에 j 를 붙이면 됨

import sys

n = int(sys.stdin.readline().rstrip())
dp = [[0] * 10 for _ in range(n+1)]

for i in range(10):
    dp[1][i] = 1

for i in range(1,n+1):
    for j in range(10):
        for k in range(j+1):
            dp[i][j] += dp[i-1][k] % 10007

print(sum(dp[n]) % 10007)