BAEKJOON : 2745, 11576, 11726, 11727

No. 2745

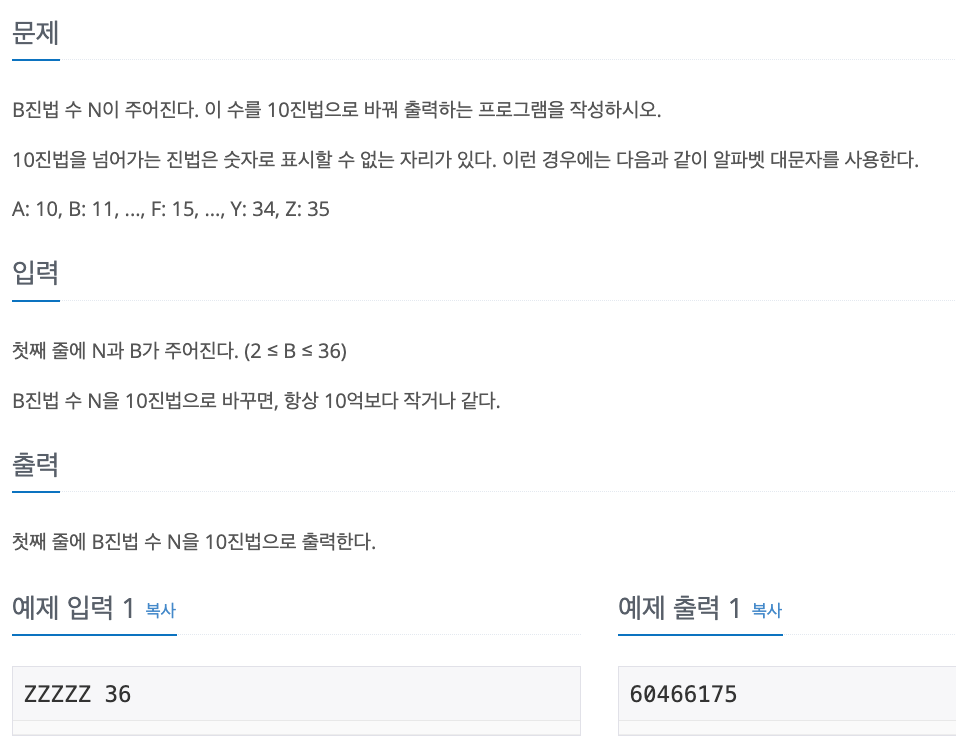
1. Problem

2. My Solution

• 2진수를 10진수로 변환하는 원리를 그대로 이용하여 B 진법만 변경
• 'A'= 10 으로 치환되었으므로 'A'를 10으로 표현하기 위해 -55

import sys

n,b = sys.stdin.readline().rstrip().split()
n = list(n)
b = int(b)

weight = 1
sum = 0

for i in n[::-1]:
    if i.isalpha():
        sum += (ord(i)-55) * weight
    else:
        sum += int(i) * weight
    weight *= b
    
print(sum)

---

No. 11576

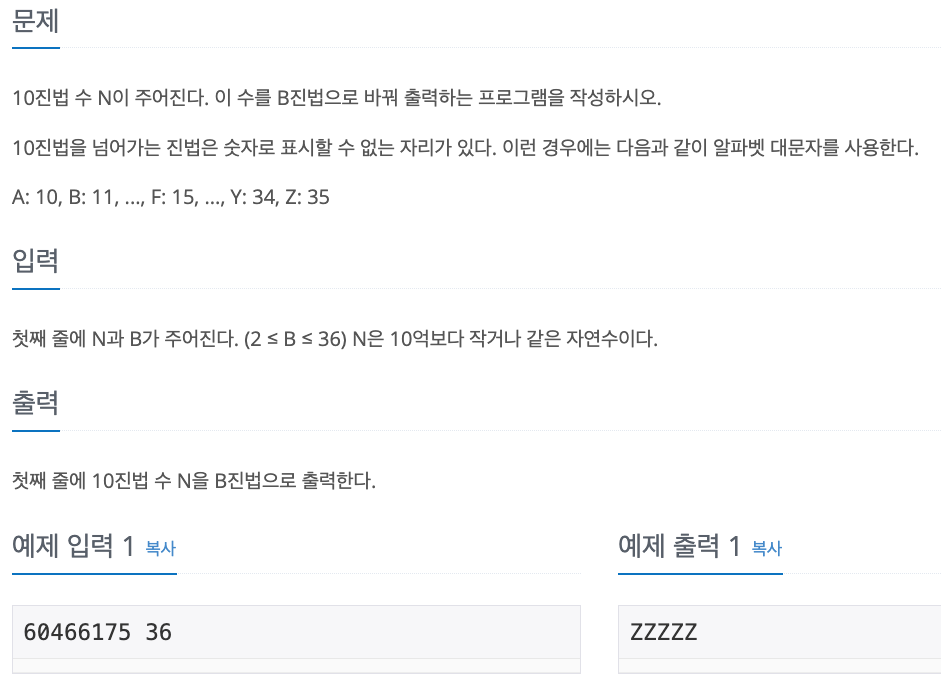
1. Problem

2. My Solution

• A진법을 10진수로 변경한뒤 다시 B진수로 변경
• 10진수로 변경한 수가 0이라면 0을 출력하고 종료

import sys

a,b = map(int,sys.stdin.readline().rstrip().split())
m = int(sys.stdin.readline().rstrip())
n = list(map(int,sys.stdin.readline().rstrip().split()))

weight = 1
decimal = 0
result = []

for i in n[::-1]:
    decimal += i * weight
    weight *= a

if decimal == 0:
    print(0)
    exit()

while(decimal != 0):
    i,j = divmod(decimal, b)

    result.append(j)
    decimal = decimal//b 

print(' '.join(list(map(str,result))[::-1]))

---

No. 11726

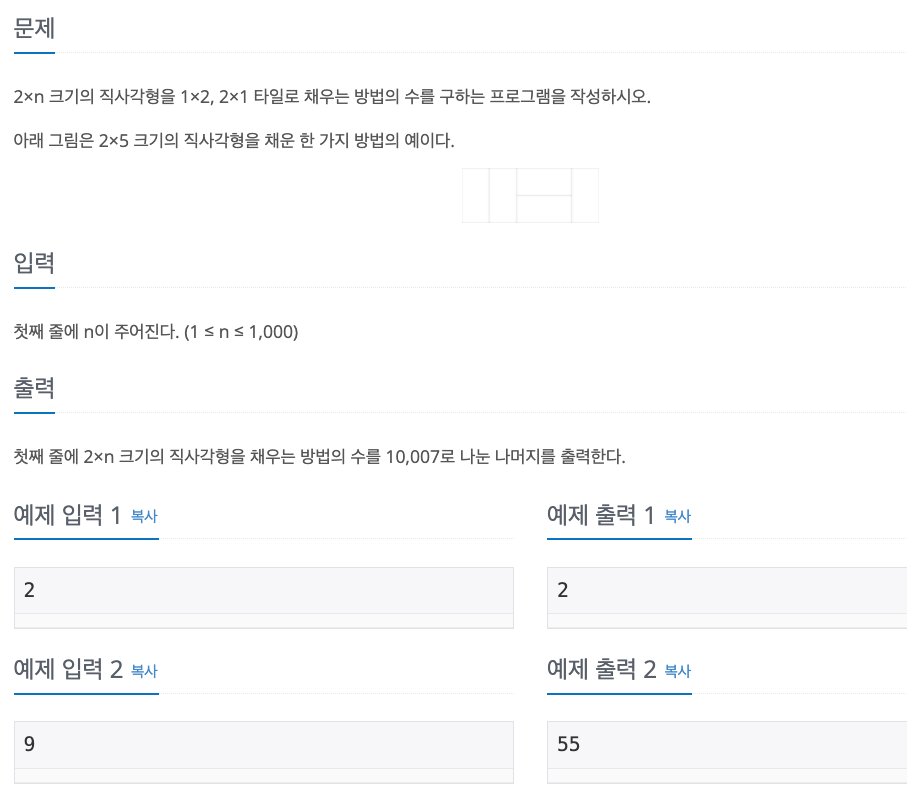
1. Problem

2. My Solution

• n = 1 부터 방법의 수를 구해서 규칙을 찾아냄
• 피보나치 수의 원리와 동일함
  
• 입력이 1000 까지이므로 단순 구현하면 런타임 에러 (RecursionError) 발생
• Dynamic Programming Top-Down 방식 구현

import sys

def solution(n):
    
    if n in dp:
        return dp[n]
    else:
        dp[n] = solution(n-1) + solution(n-2)
        return dp[n]

n = int(sys.stdin.readline().rstrip())
dp = {}
dp[1] = 1
dp[2] = 2

print(solution(n)%10007)

3. Others' Solution

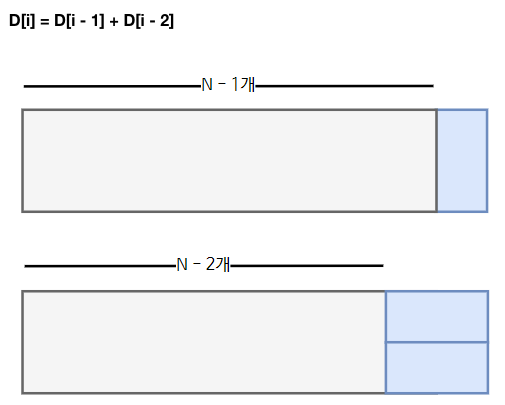
• 타일의 오른쪽 맨 끝의 모양은 2가지 경우가 존재할 수 있음
• 타일의 가로 크기 n을 1 증가시키면 2가지 경우로 나뉨

• 2 x n 크기의 타일은
  - 2 x n-1 크기의 타일에다 2x1 타일을 추가한 것
  - 2 x n-2 크기의 타일에다 1x2 타일 2개를 추가한 것

• 즉, 2 x n 타일의 가능한 경우를 구하기 위해 그 전의 답을 이용 (최적부분구조)
  

4. Learned

• 특별한 해결 원리를 찾을 수 없다면 일단 먼저 규칙을 찾아보자
• 규칙을 찾는 것 보단 해결 원리를 아는 것이 더 효율적이긴 하다
• 해결 원리 참고 유튜브

---

No. 11727

1. Problem

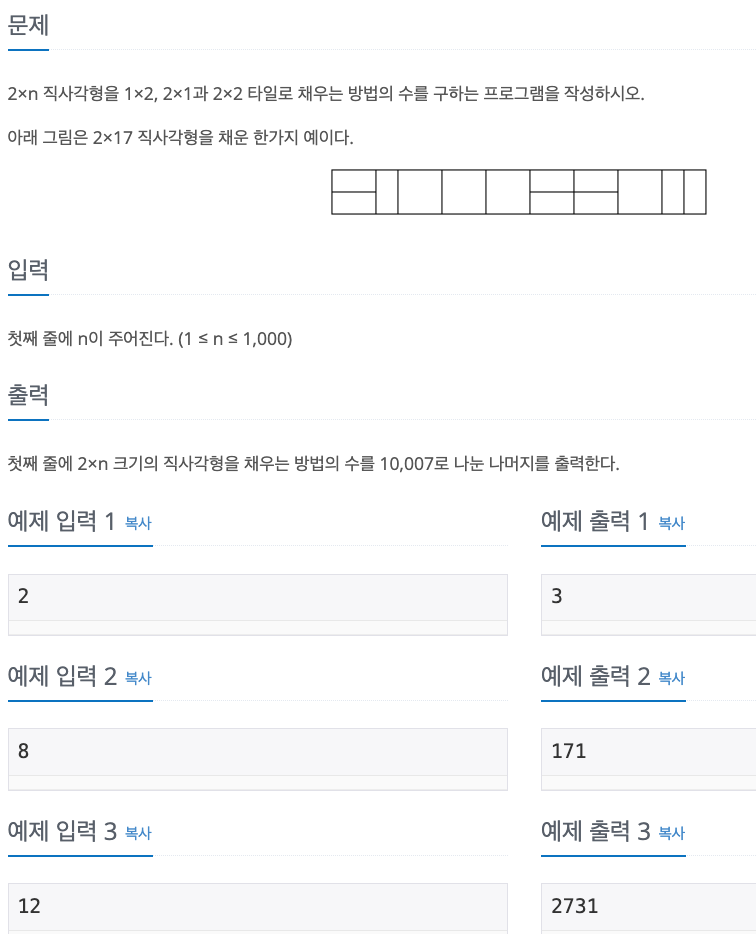
2. Others' Solution

• 타일의 오른쪽 맨 끝의 모양은 3가지 경우가 존재할 수 있음
• 타일의 가로 크기 n을 1 증가시키면 3가지 경우로 나뉨

• 2 x n 크기의 타일은
  - 2 x n-1 크기의 타일에다 2x1 타일을 추가한 것
  - 2 x n-2 크기의 타일에다 1x2 타일 2개를 추가한 것
  - 2 x n-2 크기의 타일에다 2x2 타일 1개를 추가한 것
  

• 즉, 2 x n 타일의 가능한 경우를 구하기 위해 그 전의 답을 이용 (최적부분구조)

import sys

def solution(n):
    
    if n in dp:
        return dp[n]
    else:
        dp[n] = (solution(n-1)) + (solution(n-2)) * 2
        return dp[n]

n = int(sys.stdin.readline().rstrip())
dp = {}
dp[1] = 1
dp[2] = 3

print(solution(n)%10007)