No. 17299
1. Problem
2. Others' Solutions
- 코드 길이 ↓
- 시간 ↓
import sys
n = int(sys.stdin.readline())
seq = list(map(int,sys.stdin.readline().rstrip().split()))
stack = []
result = [-1] * n
count = [0] * 1000001
for i in seq:
count[i] += 1
for i in range(n):
while stack and count[seq[stack[-1]]] < count[seq[i]]:
result[stack.pop()] = seq[i]
stack.append(i)
print(' '.join(map(str,result)))
No. 6064
1. Problem
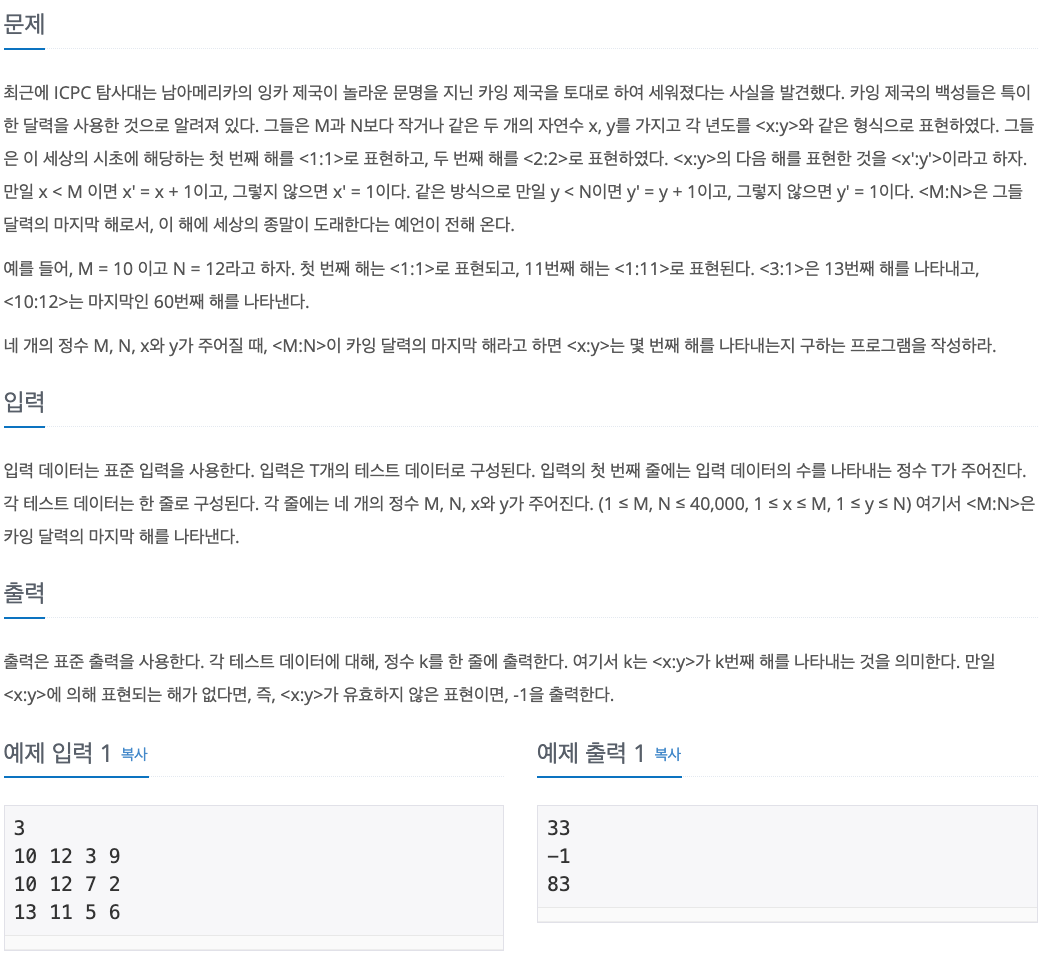
2. My Solution
- 날짜 계산 알고리즘 사용
- 브루트 포스 방식으로 1씩 증가시켜 일치하는 년도를 찾음 -> 시간초과
- 년도를 1씩 증가시키면 최악의 경우 M = 40000, N = 39999 일때 약 16억 번의 연산이 발생
import sys
test_n = int(sys.stdin.readline())
for _ in range(test_n):
m,n,x,y = map(int,sys.stdin.readline().rstrip().split())
x = x % m
y = y % n
year = 1
while(True):
if (year % m) == x and (year % n) == y:
print(year)
break
elif (year % m) == 0 and (year % n) == 0:
print(-1)
break
else:
year += 1
3. Others' Solutions
- 참고 사이트 (x,y 둘 다 말고 x 만 만족하는 경우를 생각)
- 첫 번째 방법
- 종말되는 해의 값인 m * n 이 넘어가면 종료
import sys
test_n = int(sys.stdin.readline())
for _ in range(test_n):
m,n,x,y = map(int,sys.stdin.readline().rstrip().split())
target = x - 1
year = 1 + target
x = x % m
y = y % n
while(True):
if (year % m) == x and (year % n) == y:
print(year)
break
elif year > m * n:
print(-1)
break
else:
year += m- 두 번째 방법
- 첫 번째 방법에서 종말이 되는 해의 값을 m * n 이 아닌 (m * n) // math.gcd(m,n) 이용
- 또한 while 문에서 여러 비교 연산등을 제거하여 시간을 단축
import sys
import math
test_n = int(sys.stdin.readline())
for _ in range(test_n):
m,n,x,y = map(int,sys.stdin.readline().rstrip().split())
x, y = x % m, y % n
max_year = (m * n) // math.gcd(m,n)
res = -1
for year in range(x, max_year+1, m):
if (year % n) == y:
res = year
break
print(res)
4. Learned
- math.gcd, math.lcm 을 이용하여 최대공약수 최대공배수 구할 수 있음
- 날짜 계산 문제 (% 연산 원리)의 여러가지 방법을 숙지함
ex) M N = 12 10 일때
- year = 0 으로 시작해서 결과를 출력할 때 year+1 을 출력
(x,y 를 입력받으면 각각 -1해서 12 10 전 11 9 까지만 수행)
x = 11, y = 1 이면 10,0 이 나와야함
10 % 12 = 10, 10 % 10 = 0 이므로 맞음
- 입력되는 목표 x,y 를 M,N 으로 % 연산한뒤 다시 M,N에 대입함
(12, 10 을 입력받으면 % 연산 수행수 0,0 이 되기때문에 비교할 때도 0,0 으로 비교되게끔)
M = x % M
N = y % N- (m n) // math.gcd(m,n) 해 까지 수행하는 이유
- 12 10 일때 최소 공배수인 60년도 까지만 수행하면 된다. 그 이유는 년도가 60이 되면 12와 10으로 % 연산을 했을 경우 0,0 이 나오고 이는 종말의 해인 12 10에 도달했다는 의미이다. m과 n 사이에 최대 공약수가 없다면 m * n 값이 종말의 해가 된다.