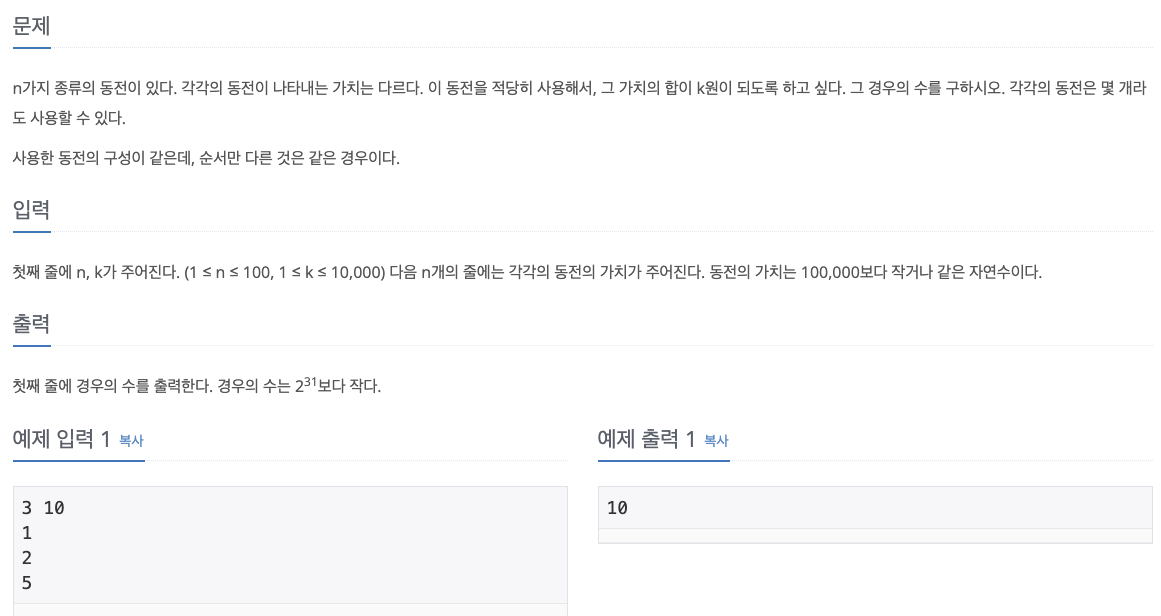
No. 2293
1. Problem
2. Others Solutions
- 첫 번째 방법
- 2차원 배열을 이용한 dp (1차원 = 사용한 동전의 수, 2차원 = k원)
- 3중 for 문으로 인해서 시간초과가 발생
import sys
n, k = map(int,sys.stdin.readline().rstrip().split())
dp = [[0]*(k+1) for _ in range(n)]
coin = []
answer = 0
for _ in range(n):
coin.append(int(sys.stdin.readline()))
for i in range(n):
for q in range(i+1):
for j in range(coin[i],k+1):
if j-coin[i] == 0:
dp[i][j] = 1
else:
dp[i][j] += dp[q][j - coin[i]]
for i in range(n):
answer += dp[i][k]
print(answer)- 두 번째 방법
- 1차원 배열을 이용한 dp (1차원 = k원)
- 1원만 사용할 때, 1원 2원만 사용할 때, 1원 2원 5원 모두 사용할 때를 누적합으로 구해냄
import sys
n, k = map(int,sys.stdin.readline().rstrip().split())
dp = [0] * (k+1)
coin = []
for _ in range(n):
coin.append(int(sys.stdin.readline()))
for i in range(n):
for cost in range(coin[i],k+1):
# cost 가 자기 자신일 때
if cost-coin[i] == 0:
dp[cost] += 1
else:
dp[cost] += dp[cost - coin[i]]
print(dp[k])
3. Learned
- dp 를 사용할 때, 2차원을 통해서 각각의 값을 가지고 있을 수 있지만 시간과 메모리가 제한적일 때는 1차원을 통해서 결과값만을 누적해서 가지고 있을 수 있음
- 참고유튜브
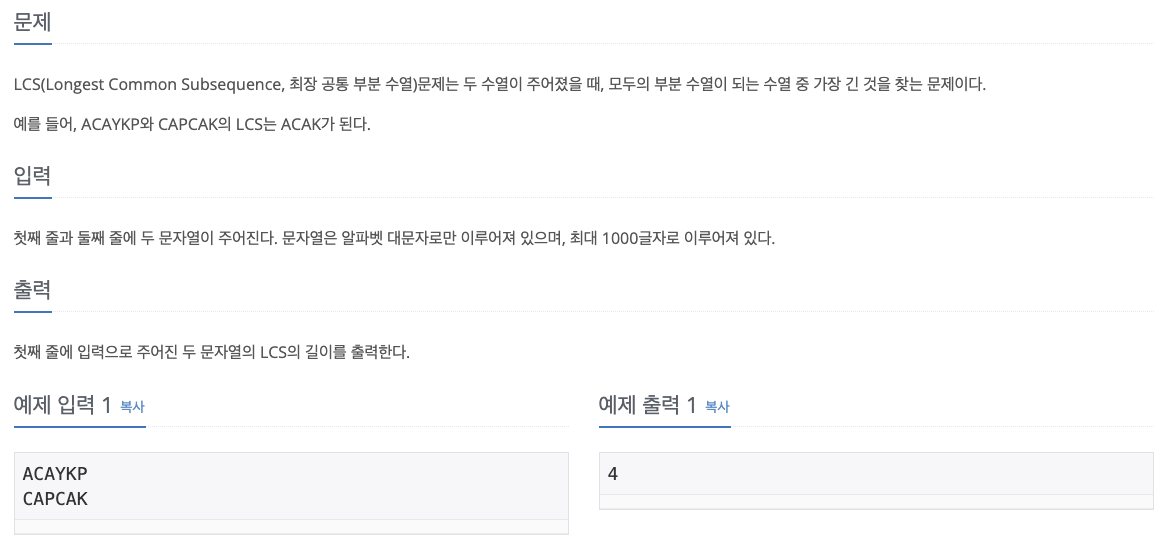
No. 9251
1. Problem
2. My Solution
- X = <x1,x2,x3,...xm>
Y = <y1,y2,y3,...yn>
-
두 문자열 X,Y 에 대한 최장공통부분순서는 아래와 같은 정리를 따른다
- xm = yn 이면 LCS의 길이는 Xm-1 과 Yn-1 의 LCS 길이보다 1 크다.
- xm != yn 이면 LCS의 길이는 Xm 과 Yn-1의 LCS 길이, Xm-1 과 Yn의 LCS 길이 중 큰 것과 같다 -
2차원 dp[i][j] 를 이용함 (i = X의 문자열길이, j = Y의 문자열길이)
-
3가지 경우로 나눌 수 있음
- i or j == 0 인 경우
- X[i] == Y[j] 인 경우
- X[i] != Y[j] 인 경우
# dp[i][j] -> i = 문자열 X에서 i번째까지 판단할 때(i번째가 마지막원소)
# -> j = 문자열 Y에서 j번째까지 판단할 때(j번째가 마지막원소)
# 0번째는 문자열이 없을 때를 나타냄. 따라서 1번부터 시작하면 됨
import sys
X = " " + sys.stdin.readline().rstrip()
Y = " " + sys.stdin.readline().rstrip()
dp = [[0] * len(Y) for _ in range(len(X))]
for i in range(len(X)):
dp[i][0] = 0
for i in range(len(Y)):
dp[0][i] = 0
for i in range(1,len(X)):
for j in range(1,len(Y)):
if X[i] == Y[j]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
print(dp[len(X)-1][len(Y)-1])
3. Learned
- LCS(최장공통부분수열) 문제에 대한 해결방법을 알게됨
- dp 문제를 풀 때, 1차원 또는 2차원의 값으로 사용할 요소를 선정하고 최적부분구조가 어디서 발생하는지를 파악해야함
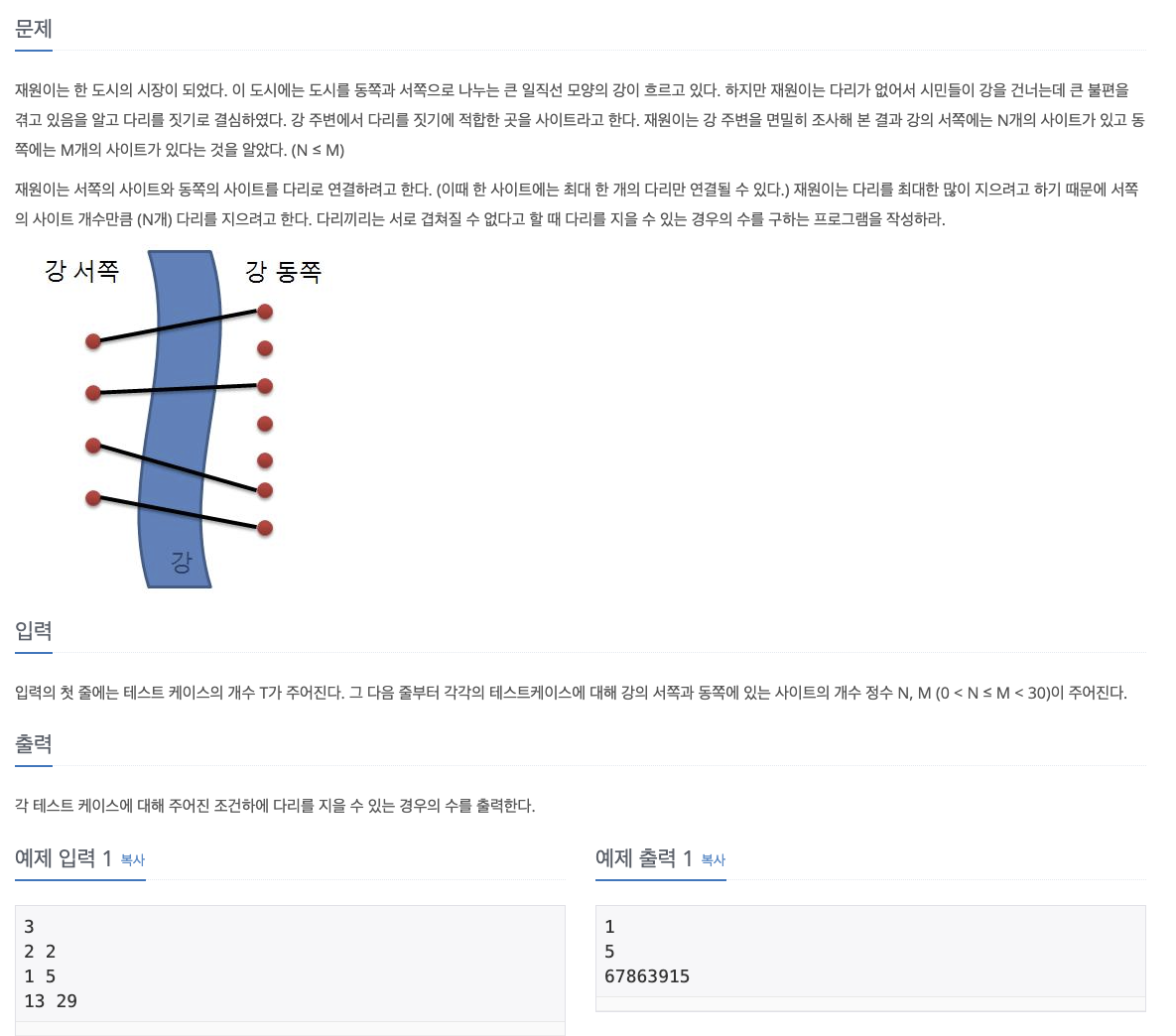
No. 1010
1. Problem
2. My Solution
- 첫 번째 방법
- 규칙을 통해 점화식을 세우는 방법
- 왼쪽의 사이트를 1차원, 오른쪽의 사이트를 2차원으로 하는 dp 를 직접 구해서 나열해봄
- 왼쪽의 사이트가 1인 경우 -> 오른쪽의 사이트 개수
- 왼쪽의 사이트와 오른쪽의 사이트의 수가같은 경우 -> 1
- 나머지 경우 -> dp[i][j] = dp[i][j-1] + dp[i-1][j-1]

import sys
test_n = int(sys.stdin.readline())
for _ in range(test_n):
n,m = map(int,sys.stdin.readline().rstrip().split())
dp = [[0]* (m+1) for _ in range(n+1)]
for i in range(1,m+1):
dp[1][i] = i
for i in range(1,n+1):
dp[i][i] = 1
for i in range(2,n+1):
for j in range(2,m+1):
dp[i][j] = dp[i][j-1] + dp[i-1][j-1]
print(dp[n][m])- 두 번째 방법
- 조합을 이용한 방법 (combinations)
- 다리가 겹치면 안되기 때문에 오른쪽 사이트에서 연결되는 순서는 아래 방향을 유지해야함 (예를들어 오른쪽에 1,2,3,4,5 사이트가 있을 때, 2번 다리를 연결했다면 3,4,5 중에 하나를 연결해야함)
- 또한 사이트는 중복될 수 없기 때문에 이러한 규칙을 생각하면 조합(Combinations) 원리와 동일함
3. Learned
- 경우의 수를 구하는 문제가 나오면 순열, 조합 등을 생각해보자
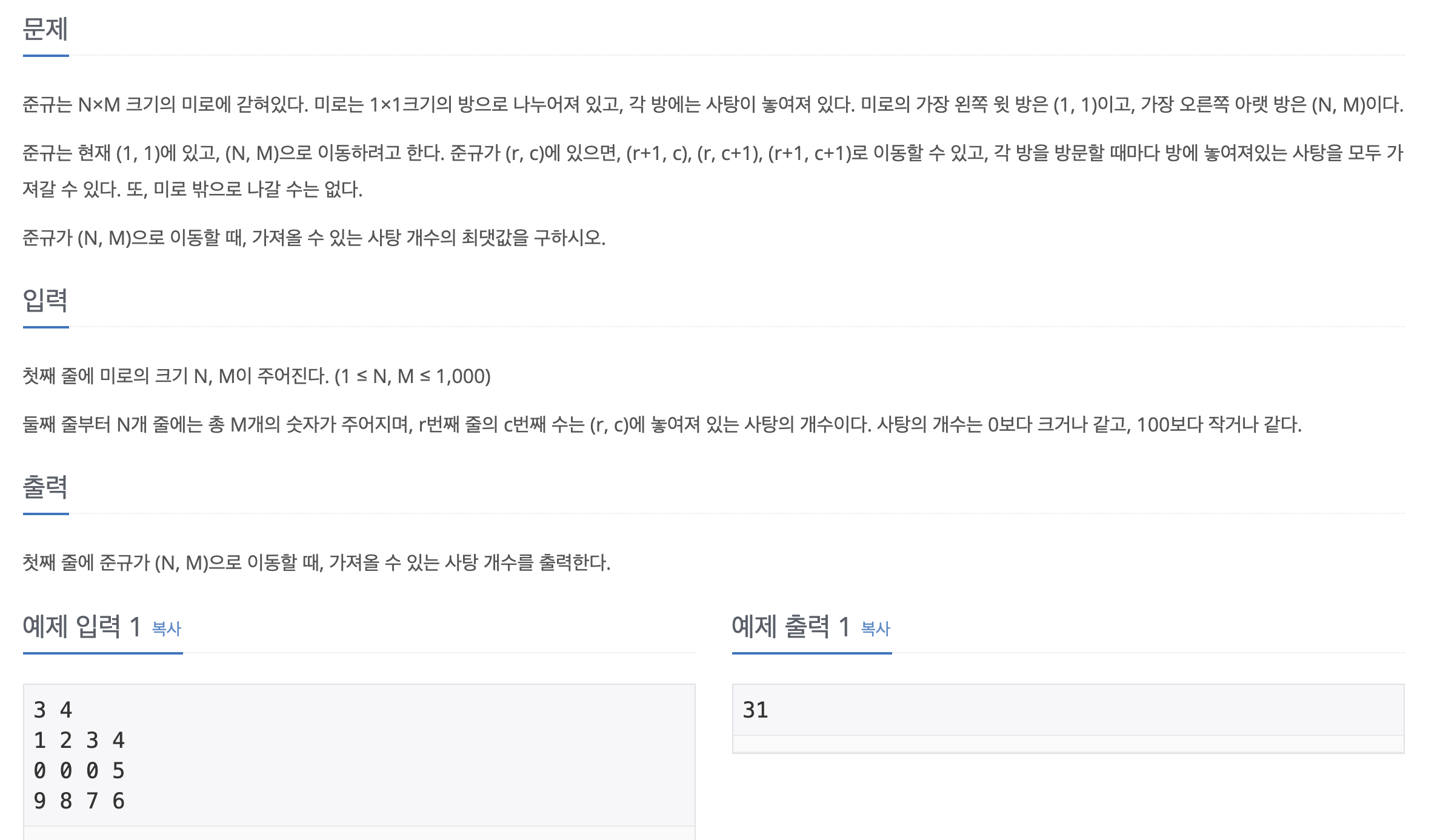
No. 11048
1. Problem
2. My Solution
- 행렬 경로 문제 해결 방법을 이용 (dp)
- 최대의 사탕을 획득하면서 n,m 까지 가는 이동 경로를 k라고 했을 때, k 경로는 마지막에
(n-1,m),(n,m-1),(n-1,m-1)중에서 (n,m) 으로 한칸 이동한 것임. 따라서 (n-1,m),(n,m-1),(n-1,m-1) 까지 최대의 사탕을 획득하는 경로에 (n,m)에 존재하는 사탕을 더하는 최적구분구조를 보이므로 dp 를 이용하여 해결 - dp[i][j] -> 미로 (i,j) 까지 갔을 때 획득할 수 있는 최대의 사탕개수
import sys
n,m = map(int,sys.stdin.readline().rstrip().split())
dp = [[0]* (m+1) for _ in range(n+1)]
miro = []
for _ in range(n):
miro.append(list(map(int,sys.stdin.readline().rstrip().split())))
for i in range(1,n+1):
for j in range(1,m+1):
dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + miro[i-1][j-1]
print(dp[n][m])No. 11066
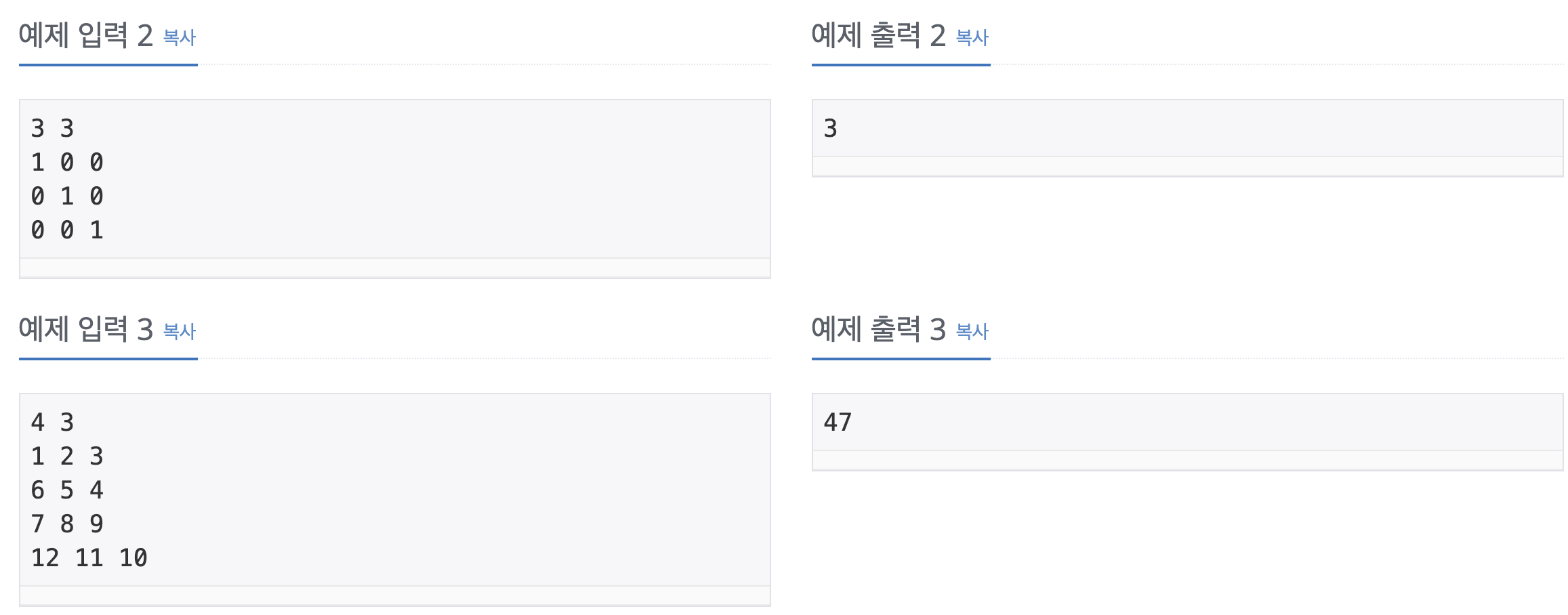
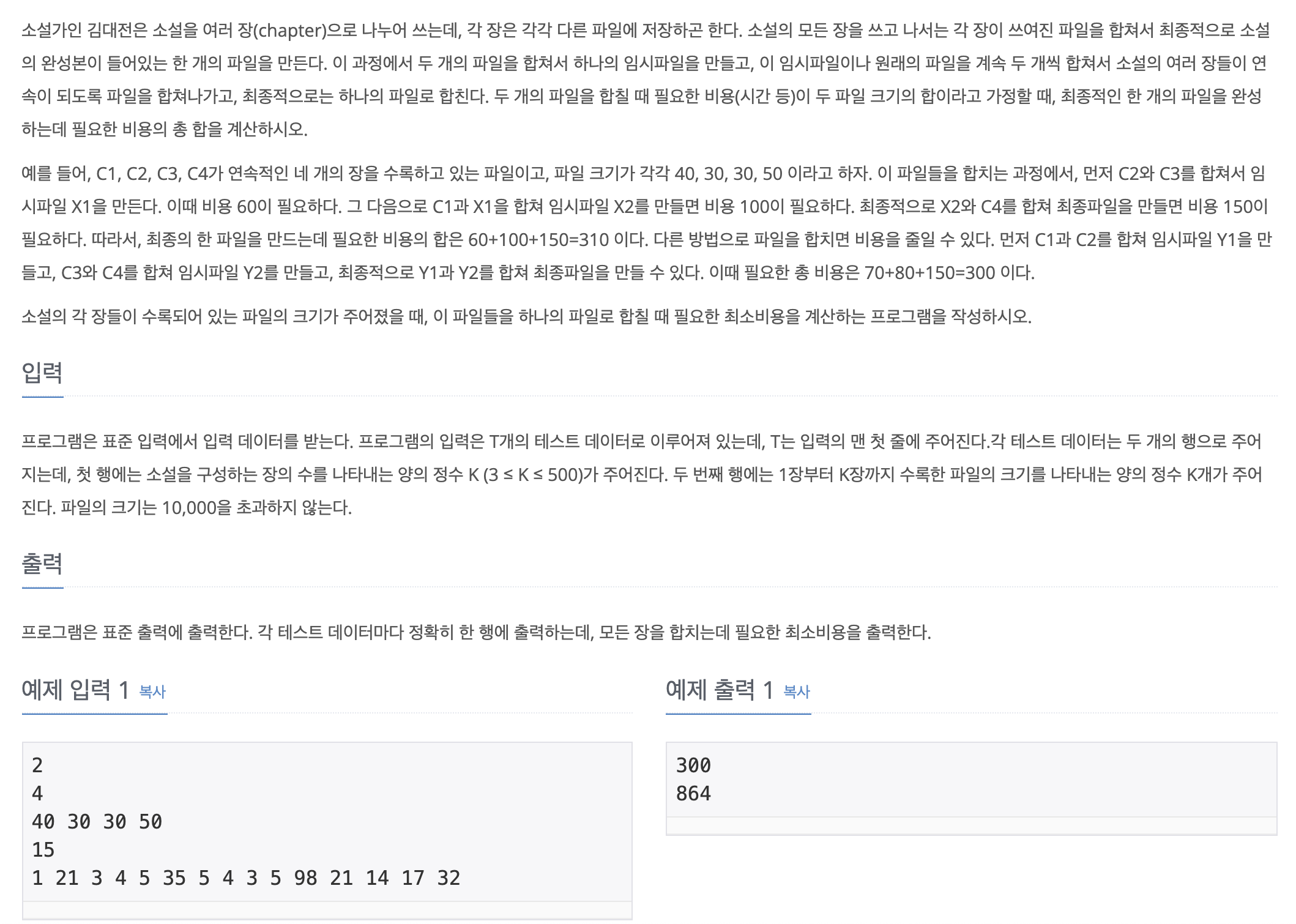
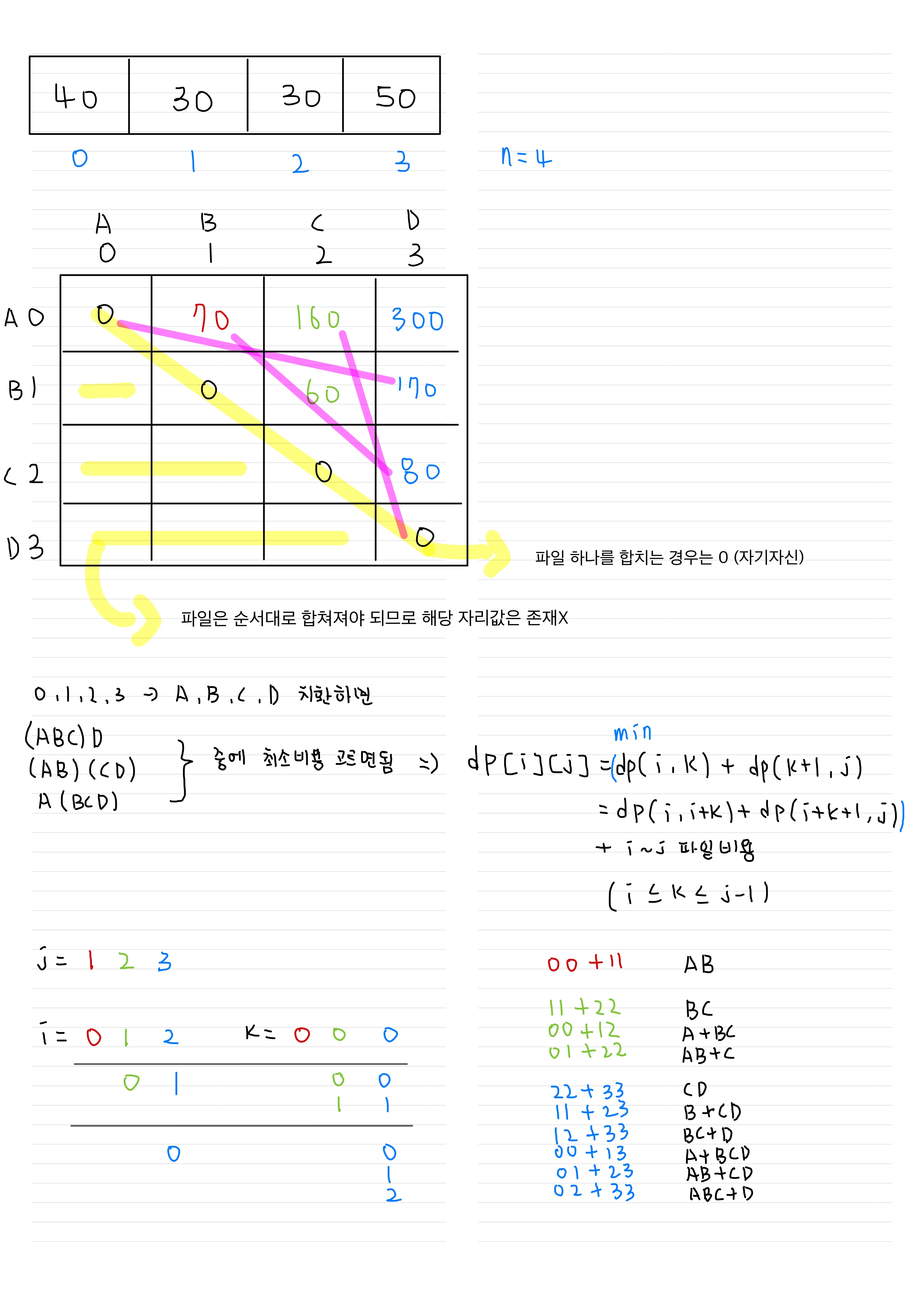
1. Problem
2. Others' Solutions
- 파일은 순서대로 합쳐져야함 (예를들어 C1, C4 가 합쳐지거나 C1, C3 가 합쳐지면 안됨)
- dp[i][j] -> i ~ j 번째 파일을 합칠 때 최소비용
- 시간복잡도 O(N^3) 이므로 python3 는 시간초과가 발생함 -> PyPy3 로 풀이 제출
import sys
import math
test_n = int(sys.stdin.readline())
for _ in range(test_n):
n = int(sys.stdin.readline())
files = list(map(int,sys.stdin.readline().rstrip().split()))
dp = [[0] * n for _ in range(n)]
for j in range(1,n):
for i in range(j-1, -1, -1):
small = math.inf
for k in range(j-i):
small = min(small, dp[i][i+k] + dp[i+k+1][j])
dp[i][j] = small + sum(files[i:j+1])
print(dp[0][n-1]) - 행렬 곱셈 순서 문제 해결 방법을 이용 (dp)
3. Learned
No. 2565
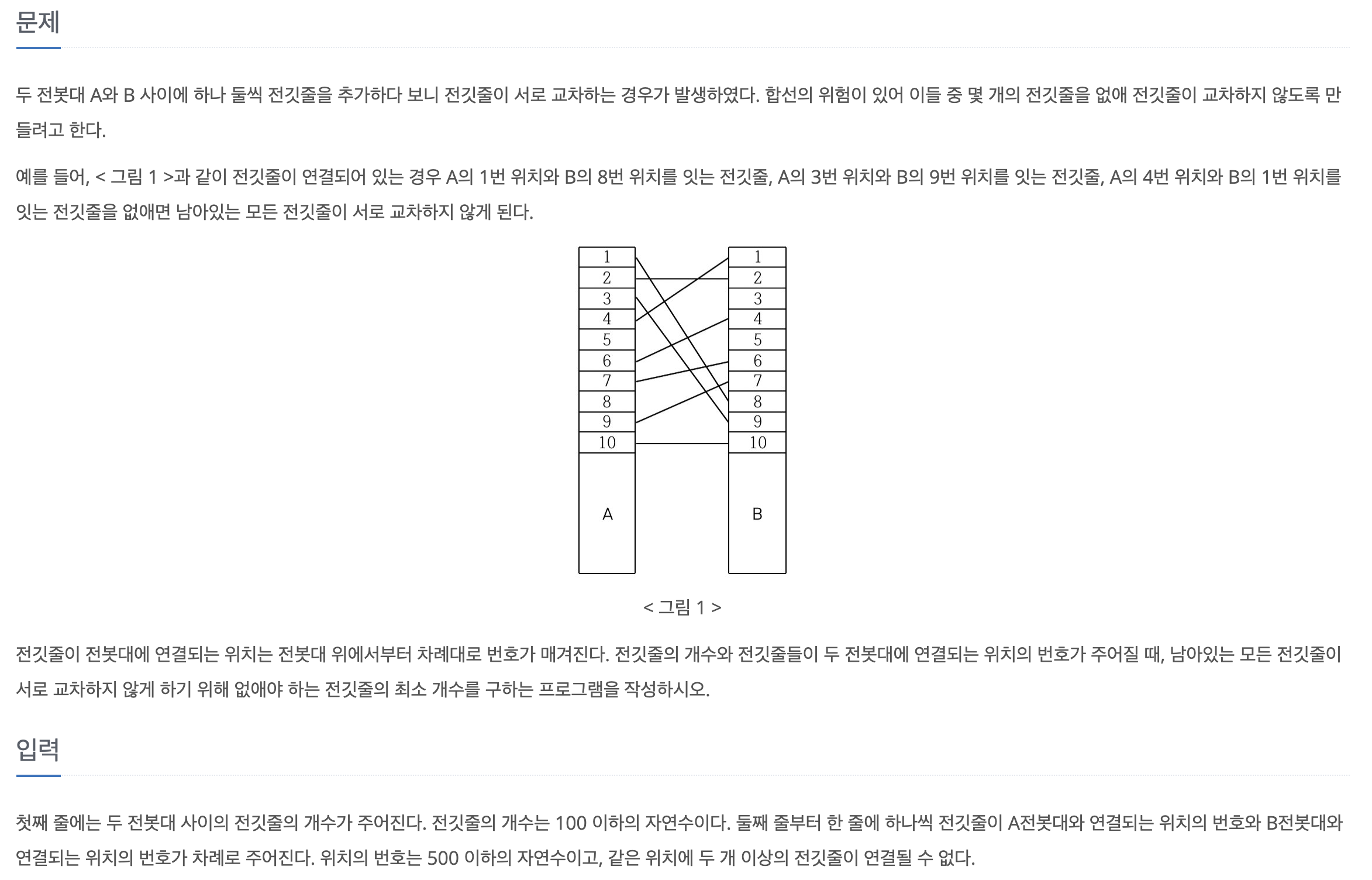
1. Problem
2. Others' Solutions
- 전깃줄의 정보에서 왼쪽의 가로등을 기준으로 오름차순 정렬했을 때, 오른쪽 가로등의 순서 또한 오름차순이어야만 전깃줄이 겹치지 않는다는 것이 보장됨
- 전깃줄이 겹치지 않도록 최소의 전깃줄을 자른다는 의미는, 또 다른 한편으로는 전깃줄이 겹치지 않도록 최대의 전깃줄을 연결하는 것을 의미함
- 오름차순 + 최대의 전깃줄 연결 => LIS (최장 증가 부분 수열) 알고리즘 이용
import sys
n = int(sys.stdin.readline())
lis = []
max_line = 0
for _ in range(n):
a,b = map(int,sys.stdin.readline().rstrip().split())
lis.append([a,b,1])
lis.sort(key=lambda x:x[0])
for i in range(n):
max_val = 0
for j in range(i):
if lis[j][1] < lis[i][1]:
max_val = max(max_val, lis[j][2])
lis[i][2] = max_val+1
max_line = max(max_line, max_val+1)
print(n - max_line)
3. Learned
- 오름차순으로 되어 있는 가장 긴(많은) 부분을 탐색할 때 LIS 알고리즘을 사용하자
- 주어진 테스트케이스에 코드를 끼워맞추지 말고, 문제의 핵심 원리를 파악하여 전체적으로 적용되는 코드를 작성하자
- 문제의 조건을 다른 관점으로도 해석할 수 있어야함 (최소의 전깃줄 자름 = 최대의 전깃줄 연결)