BAEKJOON : 2839, 10757, 1011, 11653

No. 2839

1. Problem

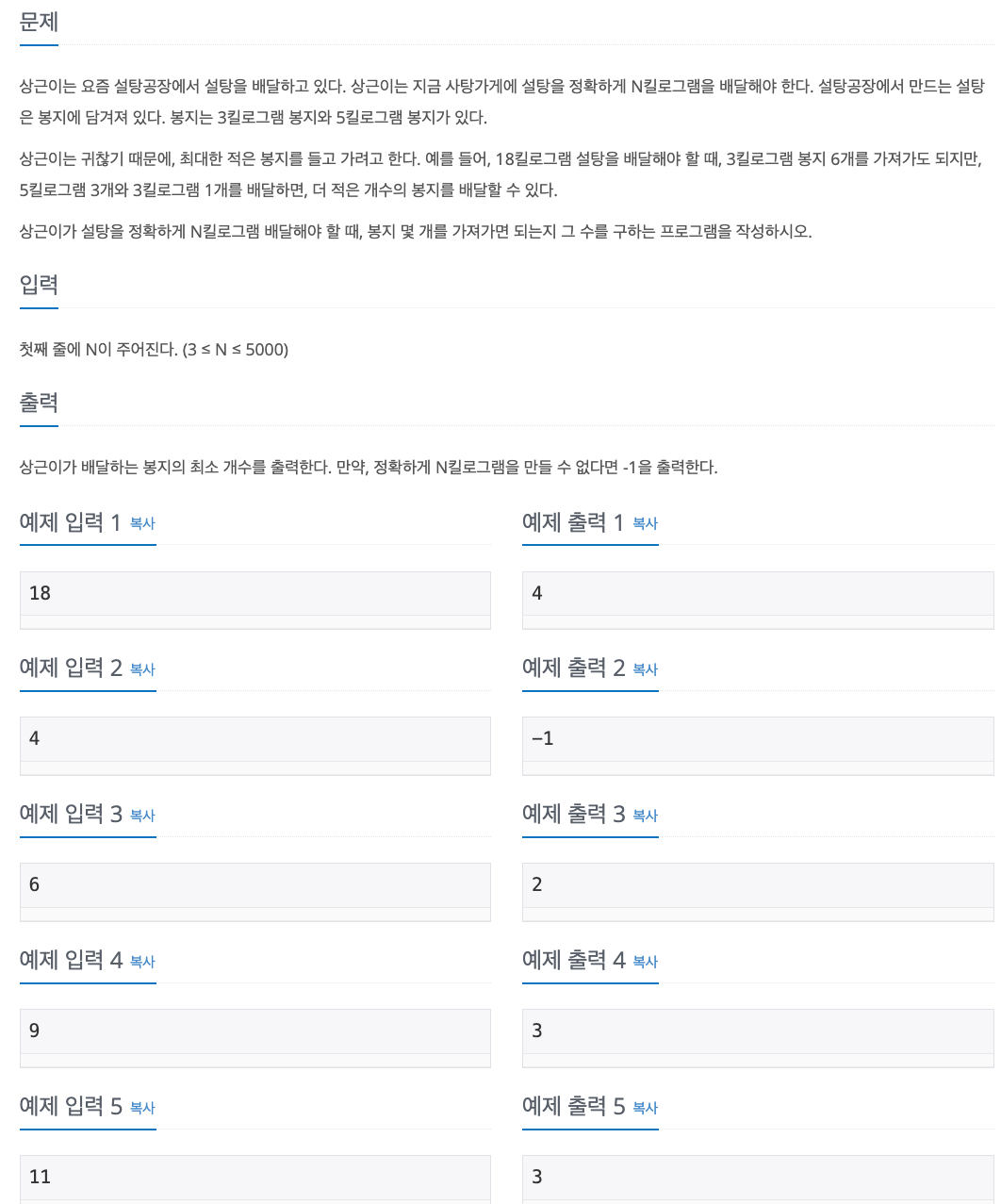
2. My Solution

• 5 킬로그램 봉지로 최대한 많이 담는 것이 중요
• 그리디 알고리즘 이용
• 5로 나눌 수 있는지 판단하고 아니면 3을 빼고 다시 5로 나눌 수 있는지 판단 (반복)

import sys

kg = int(sys.stdin.readline().strip())
count = 0

while(True):
    if kg == 0:
        break
    elif kg % 5 == 0:
        count += (kg//5)
        break
    else:
        if kg < 0:
            count = -1
            break
        kg -= 3
        count += 1

print(count)

3. Learned

• 그리디 알고리즘 - 솔루션(최선의 경우)이 될 수 있는 조건이나 상황을 파악하기

---

No. 10757

1. Problem

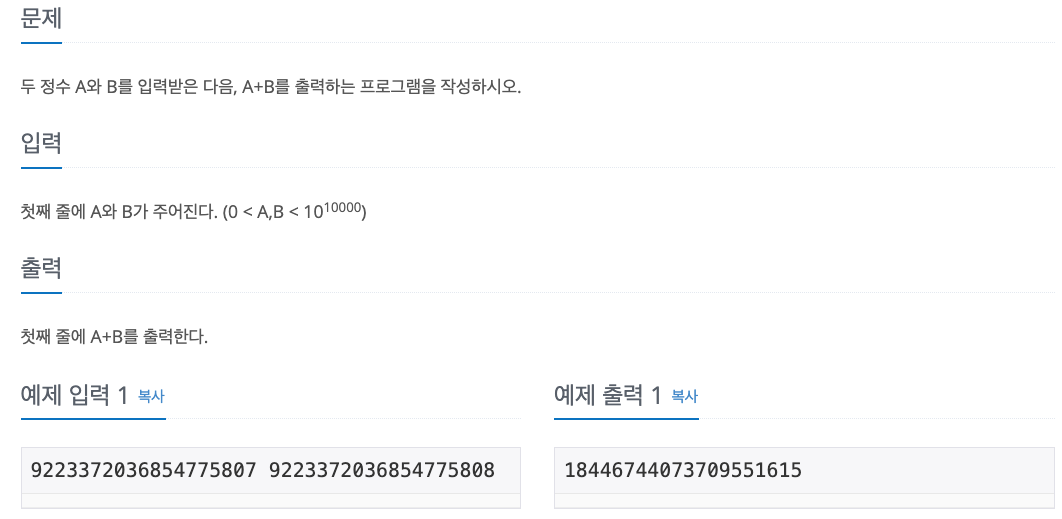
2. My Solution

• 파이썬은 큰 정수도 표현할 수 있음 (arbitrary precision)

import sys

a,b = map(int,sys.stdin.readline().strip().split())
print(a+b)

3. Others' Solutions

• 파이썬이 아닌 다른 여러 언어는 큰 정수를 표현하지 못함 (fixed precision)
• 다음과 같이 배열로 연산
  

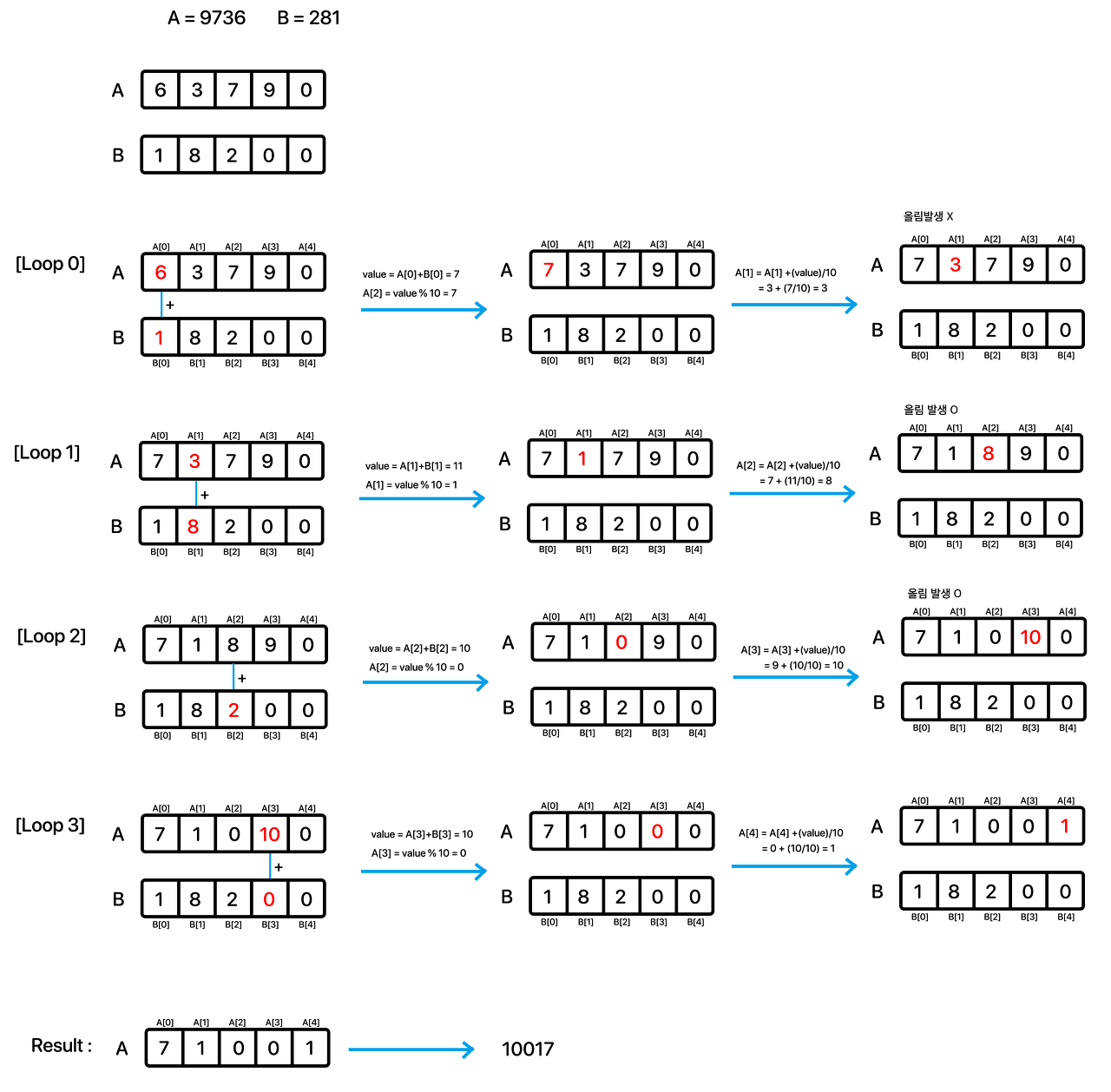
4. Learned

• 파이썬은 고정된 메모리 크기에 자료를 저장하지 않고 가변적인 메모리 크기를 사용함

---

No. 1011

1. Problem

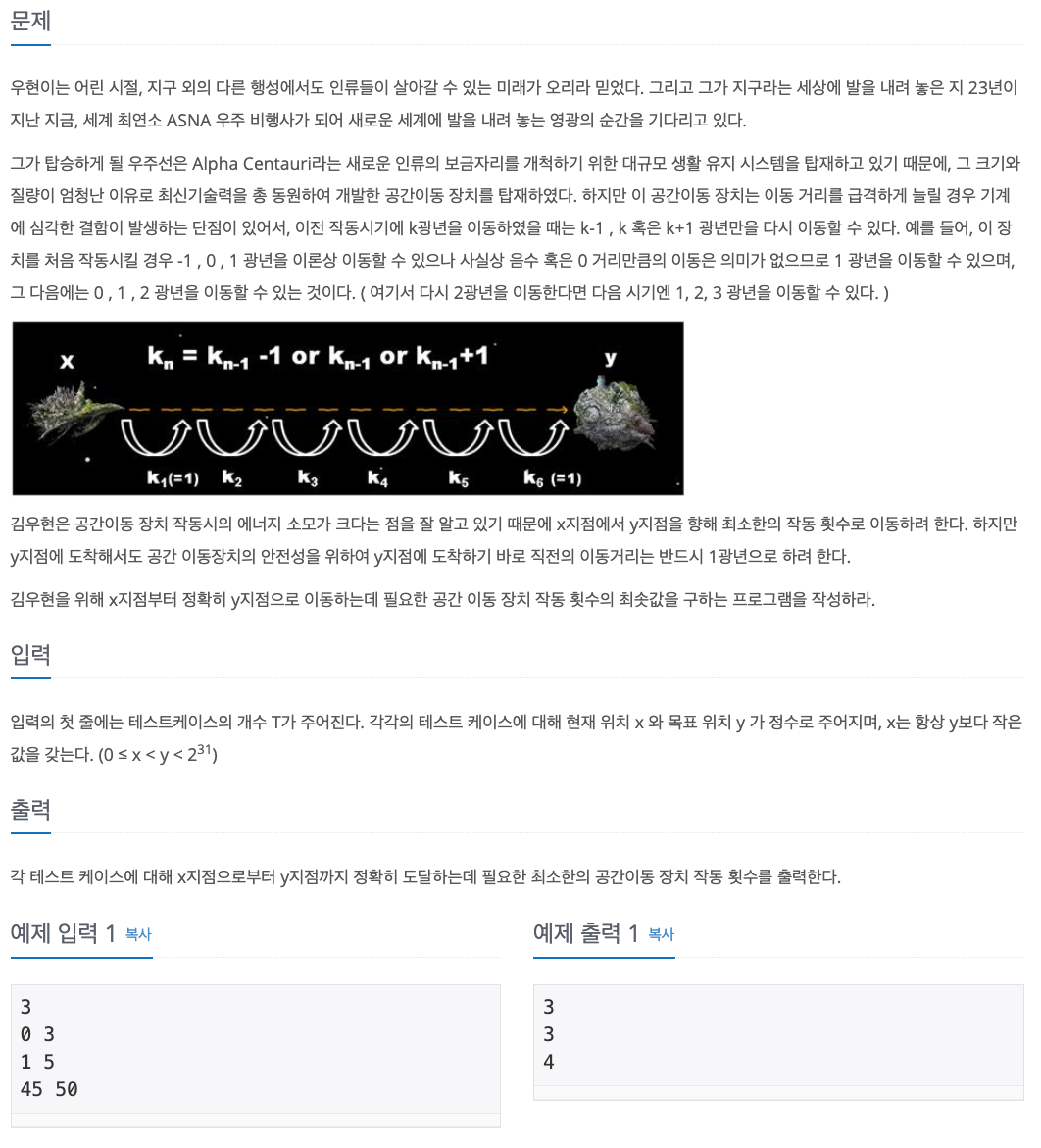
2. Others' Solutions

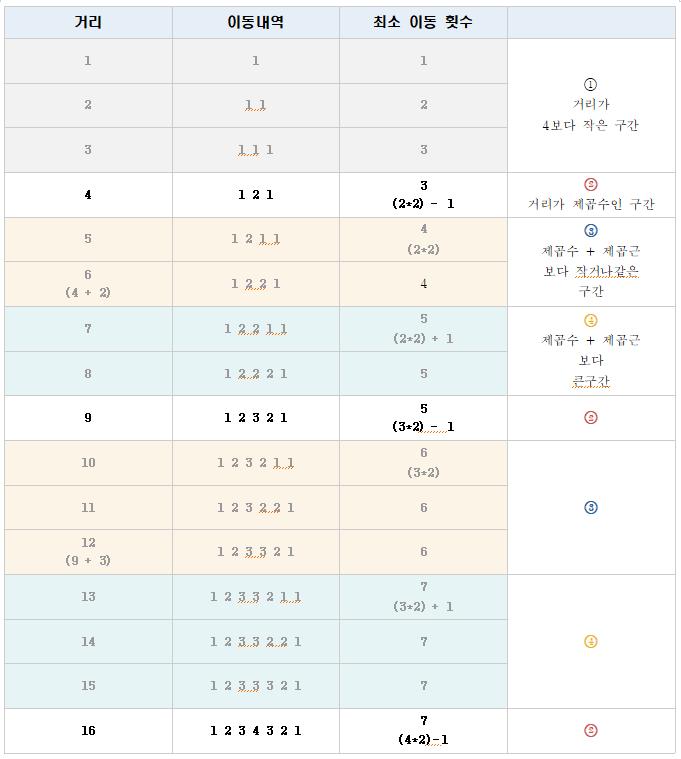
• 4,9,16 ... 제곱수에서 새로운 이동거리 나타남
• 거리가 제곱수인 구간 / 제곱수 + 제곱근 보다 작거나 같은 구간 / 큰 구간 으로 나눔

import sys
import math

test_n = int(sys.stdin.readline().strip())

for i in range(test_n):

    x,y = map(int,sys.stdin.readline().strip().split())
    distance = y - x
    sqrt = int(math.sqrt(distance))

    if distance < 4:            		# 1,2,3인 경우 해당 거리를 출력
        print(distance)

    elif distance == sqrt * sqrt:  		# 거리가 제곱수와 같은 경우
        print((sqrt * 2)-1)

    elif distance <= sqrt + (sqrt * sqrt):  	# 거리가 제곱수 + 제곱근 보다 작거나 같은 경우
        print(sqrt * 2)

    else:                       		# 거리가 제곱수 + 제곱근 보다 큰 경우
        print((sqrt * 2) +1)

3. Learned

• 제곱근을 구하는 sqrt() 함수를 위해서 math 라이브러리를 import 함
• 결과를 나열하고 모든 규칙을 찾아보자

---

No. 11653

1. Problem

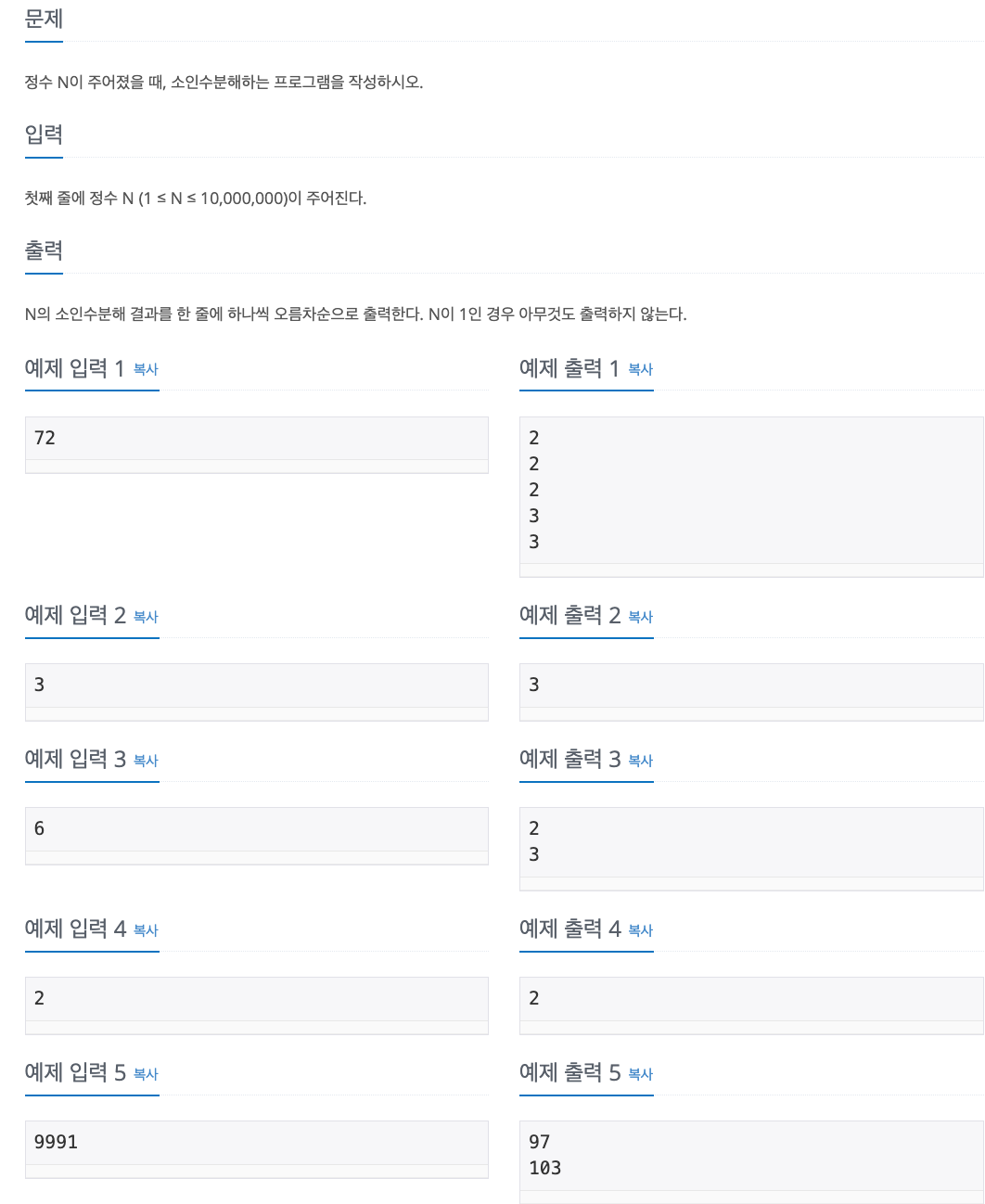
2. My Solution

• 1600ms
• 모든 수로 나눌 수 있는지 비교

import sys

n = int(sys.stdin.readline().strip())
num = 2
result = []

while(n != 1):

    if n % num == 0:
        n = n // num 
        result.append(num)
    else:
        num += 1

for i in range(len(result)):
    print(result[i])

3. Others' Solutions

• 72ms
• n = 7 일때, 2로 나뉘지 않고 3의 제곱인 9보다 작다면 4(2*2)보다는 크고 9(3*3)보다는 작은 소수

import sys

n = int(sys.stdin.readline().strip())
num = 2

while(num**2 <= n and n > 1):

    if n % num == 0:
        n = n // num 
        print(num)
    else:
        num += 1

if n!=1:
    print(n)

4. Learned

• 소인수 분해의 성질에 대해서 파악하자
• 소수를 판별할 때 해당 수의 제곱근까지만 나눠보면 판별 가능
• 9 = 1 * 9 = 3 * 3 = 9 * 1 제곱근의 곱이 중간이고 양쪽은 대칭이기 때문에 제곱근까지만 판단