선형리스트2 (Array Deque, Dual Array Deque, Rootish Array Stack)

📚 Array Deque

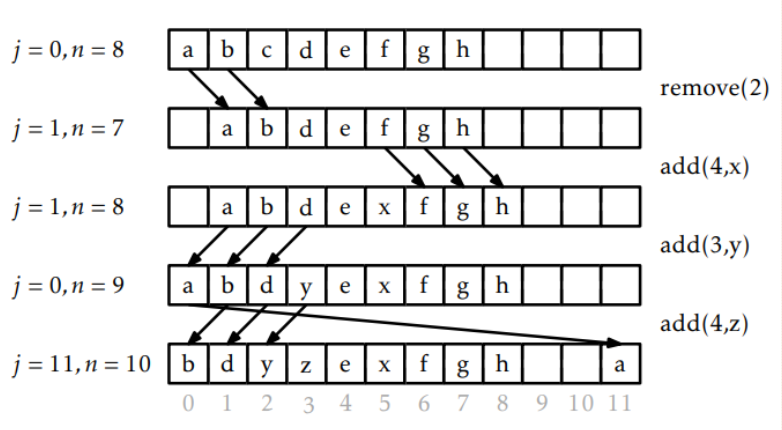
💡Array Deque이란?

배열(a) 기반으로 List인터페이스를 구현한 것.
Head, Tail 둘 중 어느곳에 원소를 조작하는 것이 더 효율적인지에 따라 인터페이스를 구현함.

• Array Deque 특징
  1. 효율적인 add, remove가 가능.
  2. Array Queue와 같은 순환 배열(circular array)기법을 사용.
  

initialize()
a <- new_array(1) # 새로운 배열을 생성하여 a변수에 저장
n <- 0 # 논리적인 순서의 처음을 나타내는 인덱스(head)
n <- 0 # 총 원소 
-> [] # 빈 배열

get(i)
#시간복잡도 O(1) 
# j(head)로 부터 i만큼 떨어진 원소를 리턴
	return a[(i + j) mod length(a)] 

set(i,x)
#시간복잡도 O(1)
	y <- a[(i + j) mod length(a)]
# j(head)로 부터 i만큼 떨어진 자리에 x 저장
	a[(i + j) mod length(a)] <- x
	return y

add(i,x)
# i의 위치에 따라 min{i, n-i} 만큼의 원소 이동이 일어나므로 시간복잡도 O(min{i, n-i})
if n = length(a) then resize() # 배열a가 꽉 차면 배열의 크기 조정
# i가 중앙보다 왼쪽이면 i왼쪽의 원소들은 왼쪽으로 한칸씩 이동할 것이므로 j를 1 감소
	if i < n/2 then
		j <- (j - 1) mod length(a)
# i보다 왼족의 원소들을 한칸식 왼쪽으로 이동
		for k in 0,1,2,... i - 1 do
        	a[(j + k) mod length(a)] <- a[(j + k + 1) mod length(a)]
    else
# i가 중앙보다 오른쪽이면 i오른쪽의 원소들을 한칸씩 오른쪽으로 이동
	    for k in n,n - 1, n - 2, ... ,i , i + 1 do
        a[(j + k) mod length(a)] <- a[(j + k - 1) mod length(a)]
# j(haed)로부터 i만큼 떨어진 자리에 x 저장
	a[(j + i) mod length(a)] <- x 
	n <- n + 1

remove(i)
# i의 위치에 따라 min{i, n-i} 만큼의 원소 이동이 일어나므로 시간복잡도 O(min{i, n-i})
x <- a[(j + i) mod length(a)]
# i가 중앙보다 왼쪽이면
if i < n/2 then
# i보다 왼쪽의 원소들을 한칸씩 오른쪽으로 이동
	for k in i,i - 1, i - 2, ..., 1 do
    	a[(j + k) mod length(a)] <- a[(j + k - 1) mod length(a)]
# i보다 왼쪽의 원소이 한칸씩 오른쪽으로 이동했기 때문에 j(head)가 1 증가
	j <- (j + 1) mod length(a)
else 
# i가 중앙보다 오른쪽이면 i보다 오른쪽의 원소들을 한칸씩 왼쪽으로 이동
	for k in i,i + 1, i + 2, ..., n - 2 do
    	a[(j + k) mod length(a)] <- a[(j + k + 1) mod length(a)]
n <- n - 1
if length(a) >= 3 * n then resize()
return x

• 🗣️ 요약 :
  ArrayDeQue는 List인터페이스를 구현한다. 이때 resize() 호출에 드는 비욜을 무시하면, get(i)와 set(i,x)는 O(1)의 시간복잡도를 가지고 add(i,x)와 remove(i)는 O(min{i, n-i})의 시간복잡도를 가진다.

📚 Dual Array Deque

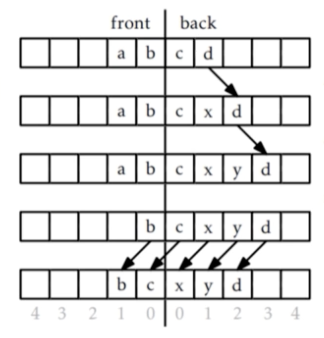
💡Dual Array Deque?

두 개의 Array Stack을 사용하여 List인터페이스를 구현한 것.

• Dual Array Deque의 특징
  1. Array Deque와 똑같은 성늘을 가짐.
  2. 단순한 데이터 구조를 결합하여 더 복잡한 데이터 구조를 생성하는 사례.
  

initialize()
	front <- ArrayStack()
    back <- ArrayStack()

get(i)
	if i < front.size() then
# front의 인덱스는 거꾸로 매겨져 있기 때문에, Index = front.size() - i - 1
		return front.get(front.size() - i - 1)
	else
# back의 경우에는 인덱스가 순차적이기 때문에, Index = i - front.size()
		return back.get(i - front.size())

set(i,x)
	if i < front.size() then
# front의 인덱스는 거꾸로 매겨져 있기 때문에, Index = front.size() - i - 1
		return front.set(front.size() - i - 1, x)
	else
# back의 경우에는 인덱스가 순차적이기 때문에, Index = i - front.size()
		return back.set(i - front.size(), x)

add(i,x)
	if i < front.size() then
# front의 인덱스는 거꾸로 매겨져 있기 때문에, Index = front.size() - i - 1
		return front.add(front.size() - i - 1, x)
	else
# back의 경우에는 인덱스가 순차적이기 때문에, Index = i - front.size()
		return back.add(i - front.size(), x)
balance() # front.size()와 back.size() 가 크게 차이나지 않도록 조정.
# add(i,x)의 시간복잡도는 balance함수가 어떻게 구현되느냐에 따라 다를 수 있지만,
# balance에 의해 front와 back의 원소 수가 거의 동일하게 유지되는 이상적인 경우를 가정하면, 
# i < n - i 일 때 (i < front.size()일 때) O(i)이고
# i >= n - i 일 때 (i >= front.size()일 때) O(n - i)이므로
# 종합하면 O(min{i, n - i})

remove(i)
	if i < front.size() then
# front의 인덱스는 거꾸로 매겨져 있기 때문에, Index = front.size() - i - 1
		x <- front.remove(front.size() - i - 1)
	else
# back의 경우에는 인덱스가 순차적이기 때문에, Index = i - front.size()
		return back.remove(i - front.size())
balance() # front.size()와 back.size() 가 크게 차이나지 않도록 조정.

balance()
# size() : return front.size() + back.size()
n <- size()
mid <- n div 2 # n을 2로 나눈 뒤 정수로 만든 값, DualArrayDeque의 중앙에 해당하는 인덱스
if 3 * front.size() < back.size() or 3 * back.size() < front.size() then
	f <- ArrayStack() # 새로운 ArrayStack을 front로 할당하고 처음부터 mid 전까지의 원소를 front에 저장
	for i in 0,1,2,... mid - 1 do
    	f.add(i, get(mid - i - 1))
    b <- ArrayStack() # 새로운 ArrayStack을 back으로 할당하고 mid로부터 mid 오른쪽의 원소들을 back에 저장
    for i in 0,1,2,... n - mid - 1 do
    	b.add(i, get(mid + i))
    front <- f
	back <- b

• 🗣️ 요약 :
  DualArrayDeQue는 List인터페이스를 구현한다. 이때 resize()와 balance() 호출에 드는 비욜을 무시하면, get(i)와 set(i,x)는 O(1)의 시간복잡도를 가지고 add(i,x)와 remove(i)는 O(min{i, n - i})의 시간복잡도를 가진다.

📚 Rootish Array Stack

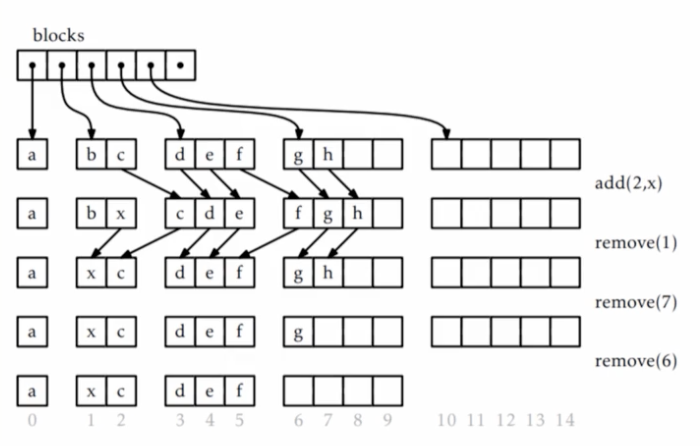
💡Rootish Array Stack 이란?

Rootish Array Stack은 앞서 나온 단점을 보안하여 List인터페이스를 구현한 것.

• 앞에 등장했던 배열 기반 데이터 구조들은 공간의 낭비가 있음.
  1. resize()의 비용이 크기 때문에 자주 호출할 수 없다.
  2. resize() 호출 후 절반 또는 1/3의 공간만이 사용됨.
• Rootish Array Stack은 𝑂(루트𝑛) 만큼의 공간이 비사용 되는 상태로 유지된다는 장점이 있음.
  

initialize()
	n <- 0
# block들을 가리킬 주소들을 ArrayStack으로 생성
	blocks <- ArrayStack()
# BlockIndex 구하는 공식
# Q) 인덱스 i가 속한 block의 인덱스 b와 block내 인덱스 j는?
i2b(i)
	 return int_value((ceil(-3.0 + sqrt(9 + 8 * i))/2.0))
# j = i - ((b(b+1)) / 2)

get(i)
	b <- i2b(i)
	j <- i - b * (b + 1) / 2
# i번째 원소는 b block의 j번째의 존재
	return blocks.get[b][j]

set(i,x)
	b <- i2b(i)
	j <- i - b * (b + 1) / 2
    y <- bloks.get(b)[j] # 기존 원소를 y에 저장해 놓고
	blocks.get[b][j] <- x # x를 b block의 j번째에 저장
	return  y

add(i,x)
# n - i - 1 개의 원소 이동이 일어나므로 O(n - i)
	r <- blocks.size()
# 총 공간이 원소 개수 + 1 보다 작으면 grow()
if r * (r + 1 ) / 2 < n + 1 then grow()
	n <- n + 1
# 마지막 원소부터 i번째 원소까지 한칸씩 오른쪽으로 이동
	for j in n - 1 , n - 2, n - 3 , ... , i + 1 do
    	set(j, get(j - 1))
	set(i,x)

# grow()함수
grow()
 	blocks.append(new_array(blocks.size() + 1))

remove(i)
# n - i 개의 원소 이동이 일어나므로 O(n - i)
	x <- get(i)
# 마지막 원소부터 i + 1번째 원소까지 한칸씩 왼쪽으로 이동
for j in i, i + 1, i + 2, ... , n - 2 do
	set(j, get(j + 1))
n <- n - 1
r <- blocks.size()
# 마지막 두 block을 제외한 나머지 block만으로 현재 원소를 모두 담을 수 잇다면 shrink()
if (r - 2)*(r - 1) / 2 <= n then shrink()
return x

# shrink()함수
shrink()
	r <- blocks.size() 
# 마지막 두 block을 제외한 나머지 block만으로 현재 원소를 모두 담을 수 잇는 조건이 성립하는 동안
# 계속 마지막 block을 삭제
	while r > 0 and (r - 2)*(r - 1) / 2 >= n do
	 	blocks.remove(blocks.size() - 1)
		r <- r - 1
# * 공간 복잡도
# shrink()의 특성상 항상 마지막 두 block은 완전히 채어지지 않은 상태로 유지됨.
# (r - 2)(r - 1) / 2 >= n인 조건에서는 계속 마지막 block을 삭제하므로, 결국 (r - 2)(r - 1) / 2 < n 가 성립
# r < (3 + 루트(1 + 8n)) / 2 = O(루트(n))
# 마지막 두 block의 사이즈는 r과 r - 1이므로 두 블록이 완전히 비었을 때 낭비되는 공간은 2r - 1 = O(루트(n))

• 🗣️ 요약 :
  RootishArrayStack는 List인터페이스를 구현한다. 이때 grow()와 shrink() 호출에 드는 비욜을 무시하면, get(i)와 set(i,x)는 O(1)의 시간복잡도를 가지고 add(i,x)와 remove(i)는 O(n - i)의 시간복잡도를 가진다.
  이때 RootishArrayStack에 의해 낭비되는 공간의 복잡도는 O(루트(n))이다.