[백준/C] 1629 - 곱셈

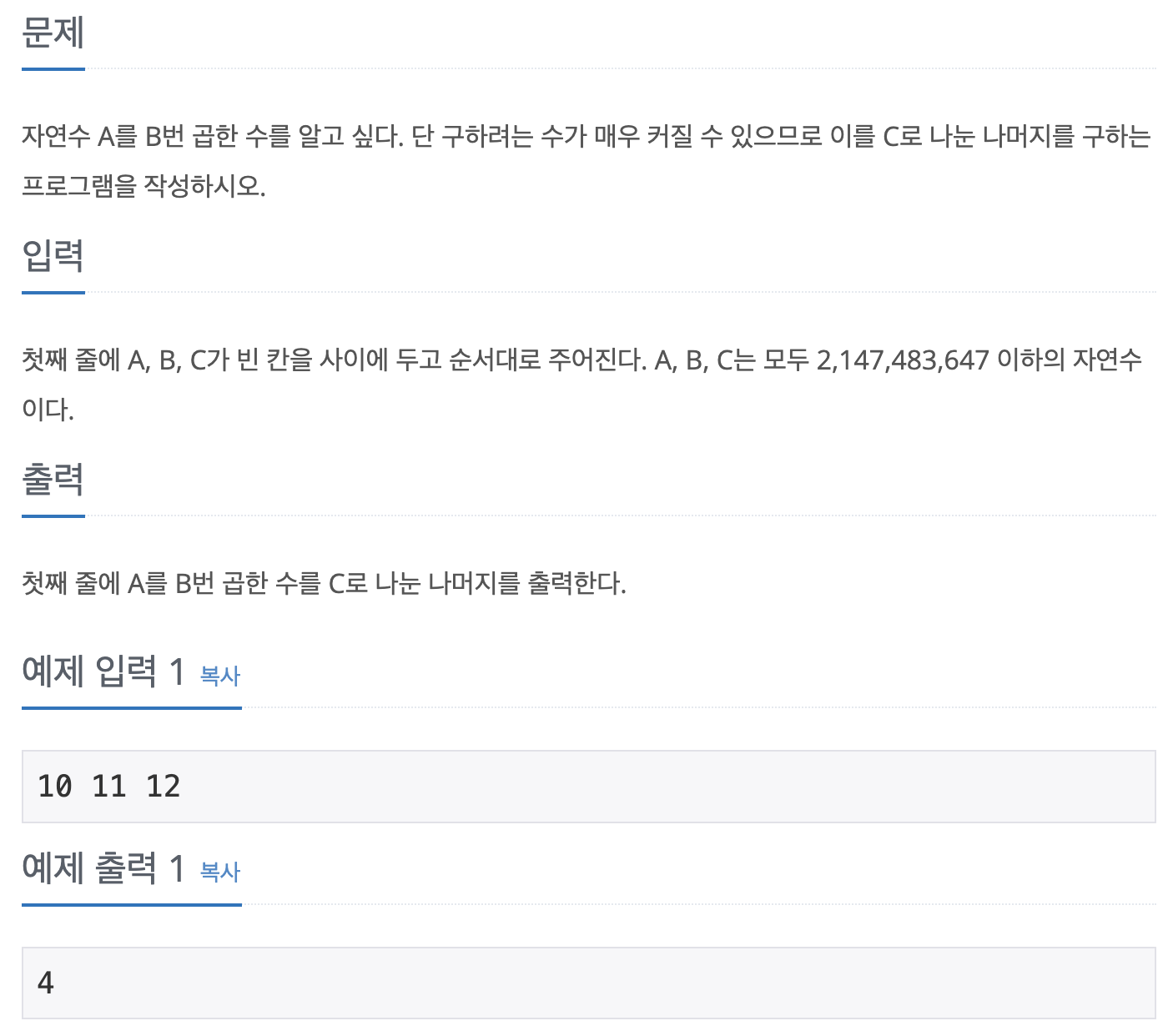
https://www.acmicpc.net/problem/1629
참고

해결 과정

int와 long long의 차이

숫자가 딱 봐도 커보이길래, long long 형을 써야 되는 줄 알았는데 알고보니 주어진 숫자 범위가 int에 들어간다.

int -2,147,483,648 ~ 2,147,483,647
long long -9,223,372,036,854,775,808 ~ 9,223,372,036,854,775,807

'A, B, C는 모두 2,147,483,647 이하의 자연수' 라고 되어 있기 때문에, int형을 쓰는 것이 가능하다. 곱한 후의 결과값만 long long형을 사용하면 된다.

분할 정복

A를 B번 곱한 수를 구할 때, 정석대로 A를 B번 곱하면 연산 횟수가 매우 많다. 특히 이 문제에서는 주어진 숫자의 범위가 매우 크기 때문에 시간 복잡도의 측면에서 굉장히 비효율적이게 된다. 따라서 이를 방지하기 위해 분할 정복을 사용해 연산한다.

이 과정에서 재귀를 사용하게 된다.

ex. 어떤 수 n을 8번 곱하는 경우
1. 정석대로 - n * n * n * n * n * n * n * n 으로 총 8번 연산하게 된다.
2. 분할 정복 - 곱하는 함수를 mul 이라고 할 때,
1) mul(8) = mul(4) mul(4) - 연산 1번
2) mul(4) = mul(2) mul(2) - 연산 1번
3) mul(2) = mul(1) * mul(1) - 연산 1번
4) mul(1) = n
이렇게 총 3번 연산하게 되어 시간복잡도가 훨씬 줄어든다.

전체 코드

#include <stdio.h>

int mul(int a, int b, int c) {
    if (b == 1)
        return a % c;

    long long res = mul(a, b / 2, c);
    res = (res * res) % c;
    if (b % 2 == 1)
        res = (res * a) % c;
    return res;
}

int main() {
    int a, b, c;
    scanf("%d %d %d", &a, &b, &c);

    printf("%d\n", mul(a % c, b, c));
    return 0;
}