[백준/C/Python] 1003 - 피보나치 함수

https://www.acmicpc.net/problem/1003

구현 과정

문제에서 주어진 피보나치 재귀함수를 호출할 때, fib(1)의 경우에는 1을 출력하고 1을 리턴하며, fib(0)의 경우에는 0을 출력하고 0을 리턴한다고 한다. 이 경우, fib(n)을 호출할 때 1과 0이 각각 몇 번 출력되는지를 구해야 한다.

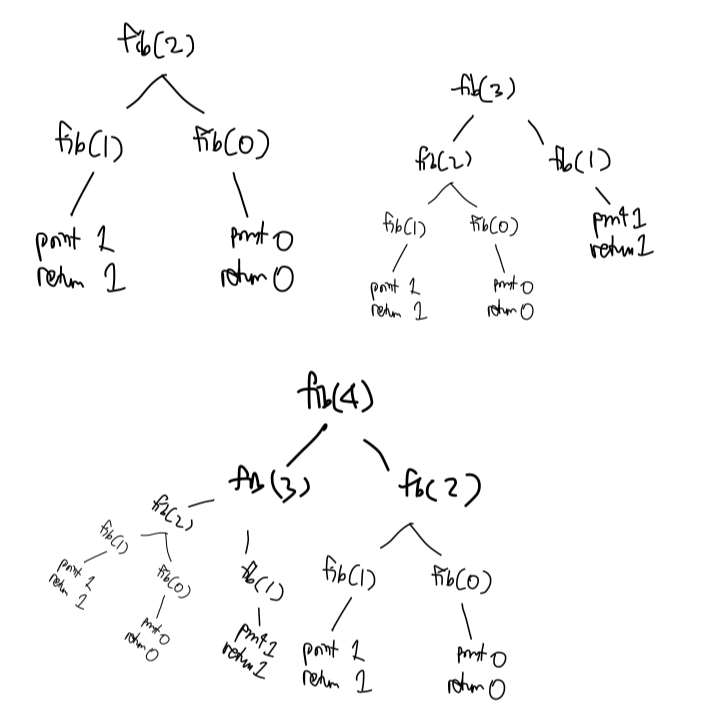
fib(2), fib(3), fib(4)에서의 재귀를 시각화해보면 아래와 같다.

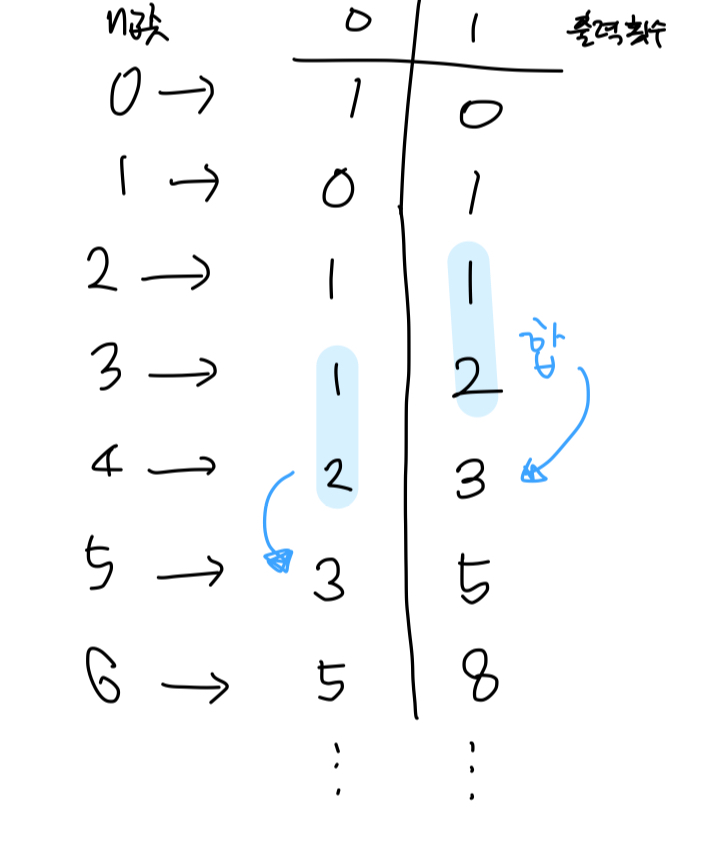
표로 정리해봤더니, 아래처럼 앞의 두 순서 개수의 합이 현재 개수가 되는 규칙이 보였다. 0이 나타나는 횟수, 1이 나타나는 횟수 각각 피보나치 수열이다. 0 출력 횟수의 피보나치 수열이 1 출력 횟수의 피보나치 수열보다 한차례 늦게 진행된다는 특징이 있다.

따라서 각각을 피보나치 수열로 구현해주면 된다. 이 문제의 경우에는 n이 최대 40까지 가능하기 때문에 fib 함수에서 미리 40번째까지 계산해두어도 문제 될 것이 없다.

C로 구현하는 경우, fib()함수를 선언하기 전에 전역변수로 각 n에 대해 0이 등장하는 횟수, 1이 등장하는 횟수를 저장해둘 int count0[41], int count1[41]을 선언해준다.

파이썬으로 구현하는 경우, 리스트의 인덱스에 접근하려면 그 인덱스가 미리 존재해야 된다. 이를 위해 count0 = [0] * 41 이런 식으로 초기화해주면서 선언해줘야 한다.

fib() 함수에서는
1. (C인 경우) n=0, n=1인 경우를 따로 초기화해주고
2. n=2부터 n=40까지는 재귀를 이용해 계산한다.

전체 코드

C

#include <stdio.h>

int count0[41];
int count1[41];

void fib() {
    count0[0] = 1;
    count1[0] = 0;
    count0[1] = 0;
    count1[1] = 1;

    for (int i = 2; i <= 40; i++) {
        count0[i] = count0[i - 1] + count0[i - 2];
        count1[i] = count1[i - 1] + count1[i - 2];
    }
}

int main() {
    int t;
    scanf("%d", &t);

    fib();

    while (t--) {
        int n;
        scanf("%d", &n);
        printf("%d %d\n", count0[n], count1[n]);
    }
    return 0;
}

Python

count0 = [0] * 41
count1 = [0] * 41

count0[0] = 1
count1[1] = 1

for i in range(2, 41):
    count0[i] = count0[i-1] + count0[i-2]
    count1[i] = count1[i-1] + count1[i-2]

t = int(input())

for _ in range (t):
    n = int(input())
    print(count0[n], count1[n])