그래프(Graph)란 무엇인가?

그래프(Graph)란?

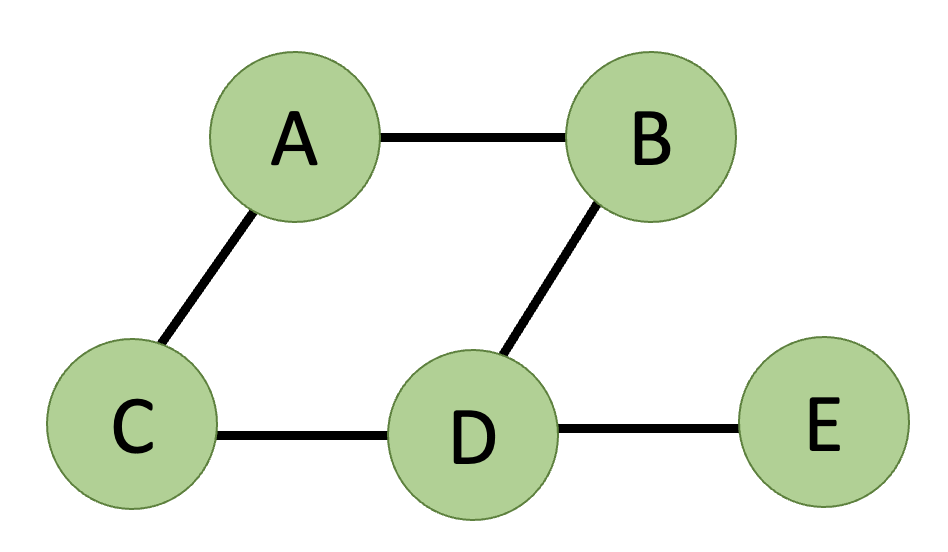
• 정의 : 그래프란 ,수학자 오일러가 만든 “그래프 이론” 의 개념을 기초로 구성된 자료구조로 서로 연결되어있는 원소간의 관계를 표현한 자료구조 이다.

---

그래프(Graph) 용어 정리

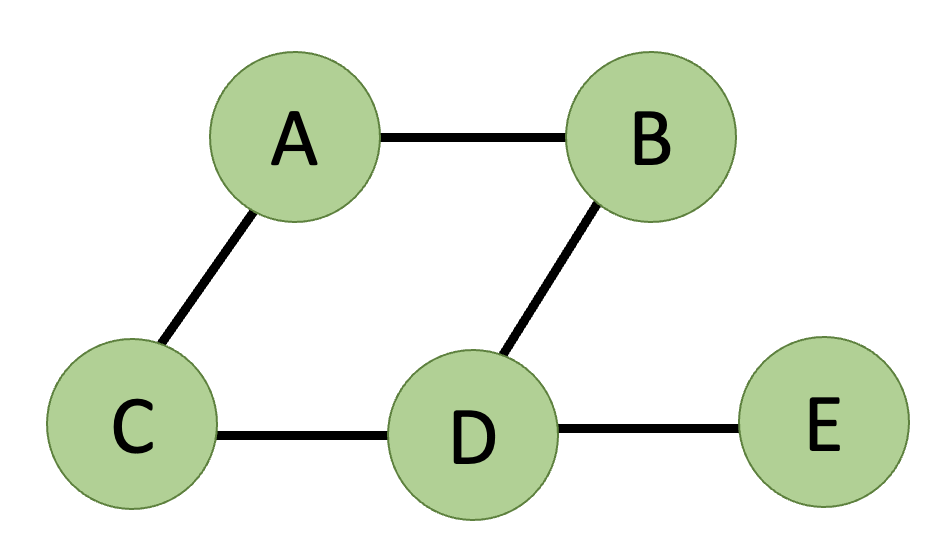
• 녹색 동그라미 : 정점 ( Vertex )
• 검정색 실선 : 간선 ( Edge )

---

그래프(Graph)의 특징

• 그래프는 네트워크 모델 이다.
• 2개 이상의 경로가 가능하다.
• 루트 노드라는 개념이 없다.
• 부모-자식 관계라는 개념이 없다.
• 그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
• 그래프는 크게 방향 그래프와 무방향 그래프가 있다.
• 포털 사이트의 검색 엔진, SNS에서 사람들과의 관계, 네비게이션 (길찾기) 등에서 그래프 자료구조가 사용된다.
  
  

---

그래프(Graph)의 종류

무방향 그래프

• 무방향 그래프는 간선의 방향이 없어 서로간 왕복이 가능한 그래프 이다.
  

방향 그래프

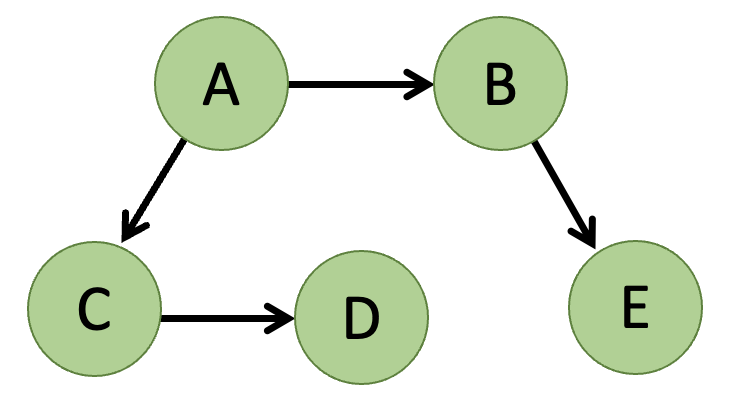
• 방향 그래프는 간선의 방향이 존재하는 그래프 이다.

ex)

• SNS 팔로우
  - 5명의 유저 팔로우 관계에서 A → B → E 관계로 팔로우 하고 있다
  ⇒ A는 B를 통해 E를 건너 볼 수 있다.

  
  

• 방향 그래프는 간선이 추가되면

  • 한쪽 정점에서 다른 정점으로 이동은 가능 (A → B)
  • 하지만 반대로의 이동은 불가능 ( B → A)

이외의 연결, 비연결, 사이클, 비순환, 완전 그래프 등이 존재한다.

---

그래프(Graph)의 구현 방식

그래프의 구현 방식에는 2가지 방식으로 나뉜다.

• 연결 리스트 기반 그래프

  • 연결 리스트 기반 그래프는 연결 리스트 배열을 만들고 다음과 같이 표현한다.

    

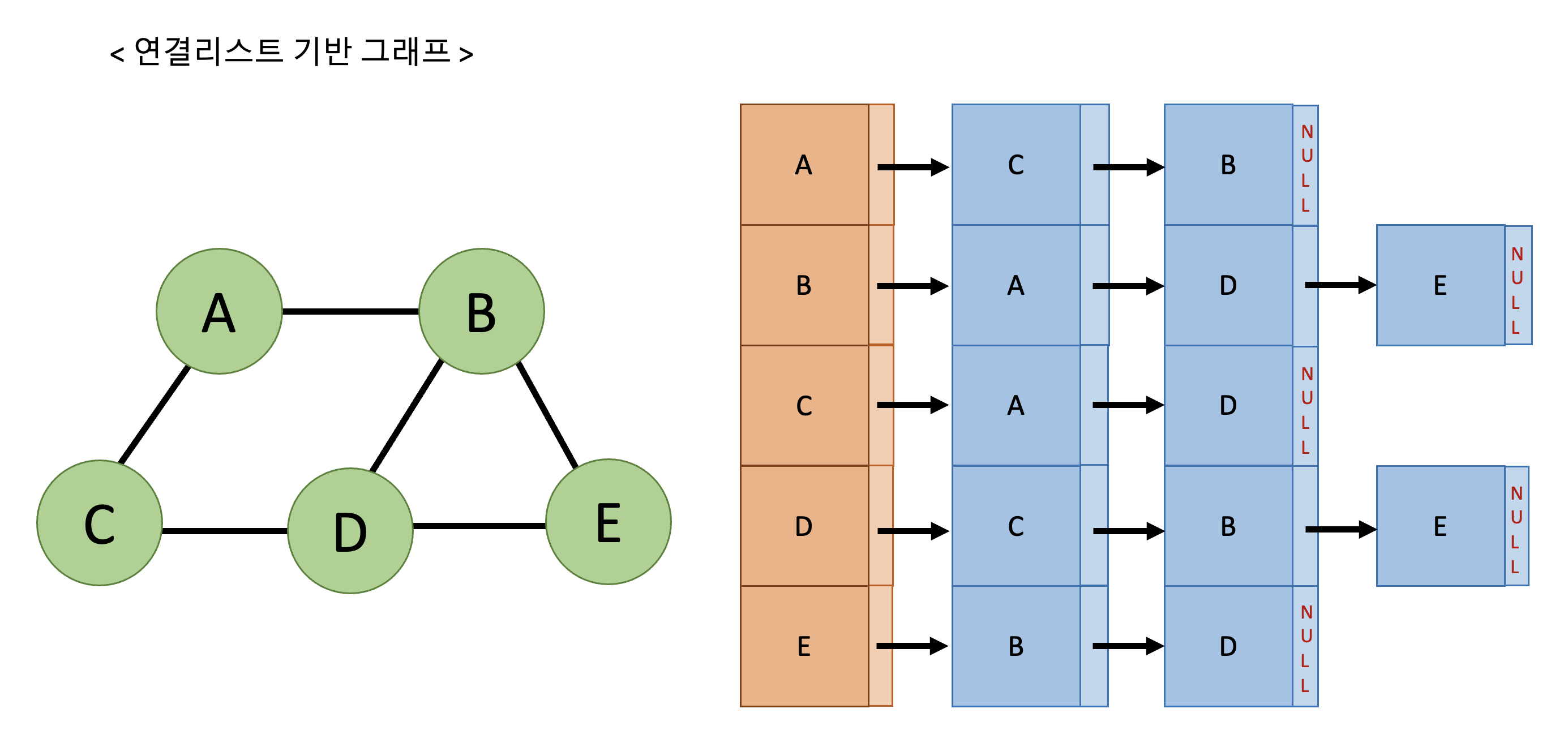
  • 연결 리스트 기반 그래프 장단점

    • 장점

      • 정점 연결 정보 탐색시 O(n)의 시간이면 가능 n = 간선의 갯수
      • 필요 만큼의 공간만 사용하기 때문에 공간 낭비가 적다

    • 단점

      • 특정 두 점이 연결되었는지 확인 시 행렬 기반에 비해 시간이 오래걸린다 (검색 속도가 느림)
      • 구현이 비교적 어렵다.

• 행렬 기반 그래프
  • 인접 행렬 기반 그래프는 이차원 배열을 만들고
  • 연결된 곳은 1
  • 연결되지 않은 곳은 0
    ⇒ 같이 표현한다.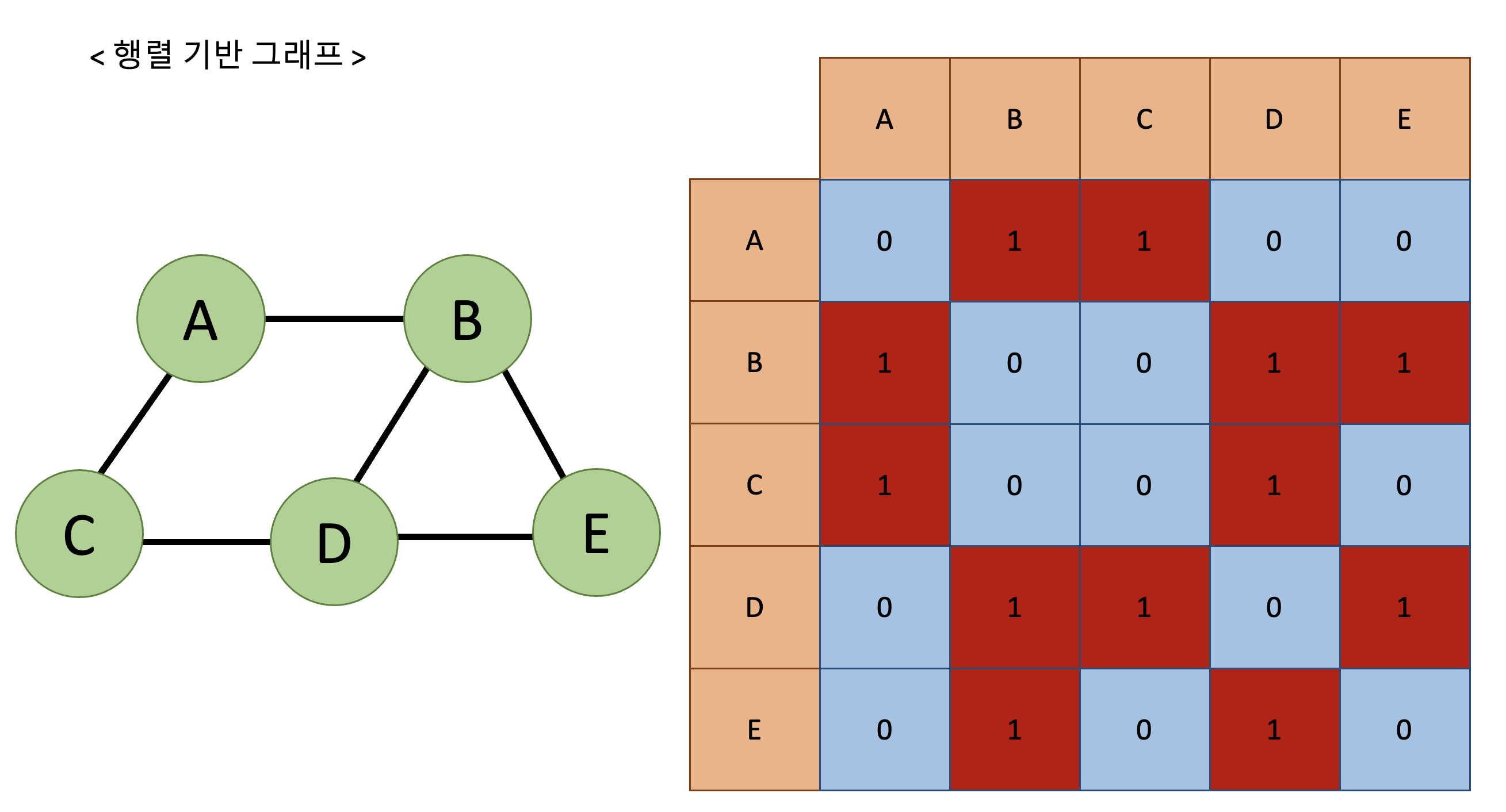

    

• 행렬 리스트 기반 그래프 장단점

  • 장점

    • 2차원 배열에 간선 정보를 담기 때문에 두점의 연결 정보 조회시 O(1) 시간 복잡도가 걸린다.
    • 구현이 비교적 간편하다.

  • 단점

    • 모든 정점에 대한 간선 정보를 삽입하여야 하기 때문에 O(n^2) 시간 복잡도가 걸린다.
    • 무조건적으로 2차원 배열이 필요하기 때문에 필요 이상의 공간이 낭비된다.

그래프를 가지고 위의 2가지 방식으로 표현이 가능하다.

---

그래프(Graph)의 탐색

 그래프 탐색

• 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
  • Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지

깊이 우선 탐색 (DFS, Depth-First Search)

• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

1. 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사

2. 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함

3. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함

4. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함

5. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림

너비 우선 탐색 (BFS, Breadth-First Search)

• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법

1. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

2. 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것

3. 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함

---