(Swift) 3053 택시 기하학

3053번: 택시 기하학

// 택시 기하학

let R = Double(readLine()!)!

print(R * R * Double.pi)
print(R * R * 2)

1. 택시 기하학의 정의만 파악하면 코드 자체는 너무나 간단합니다.
2. 아래 그림을 봅시다.
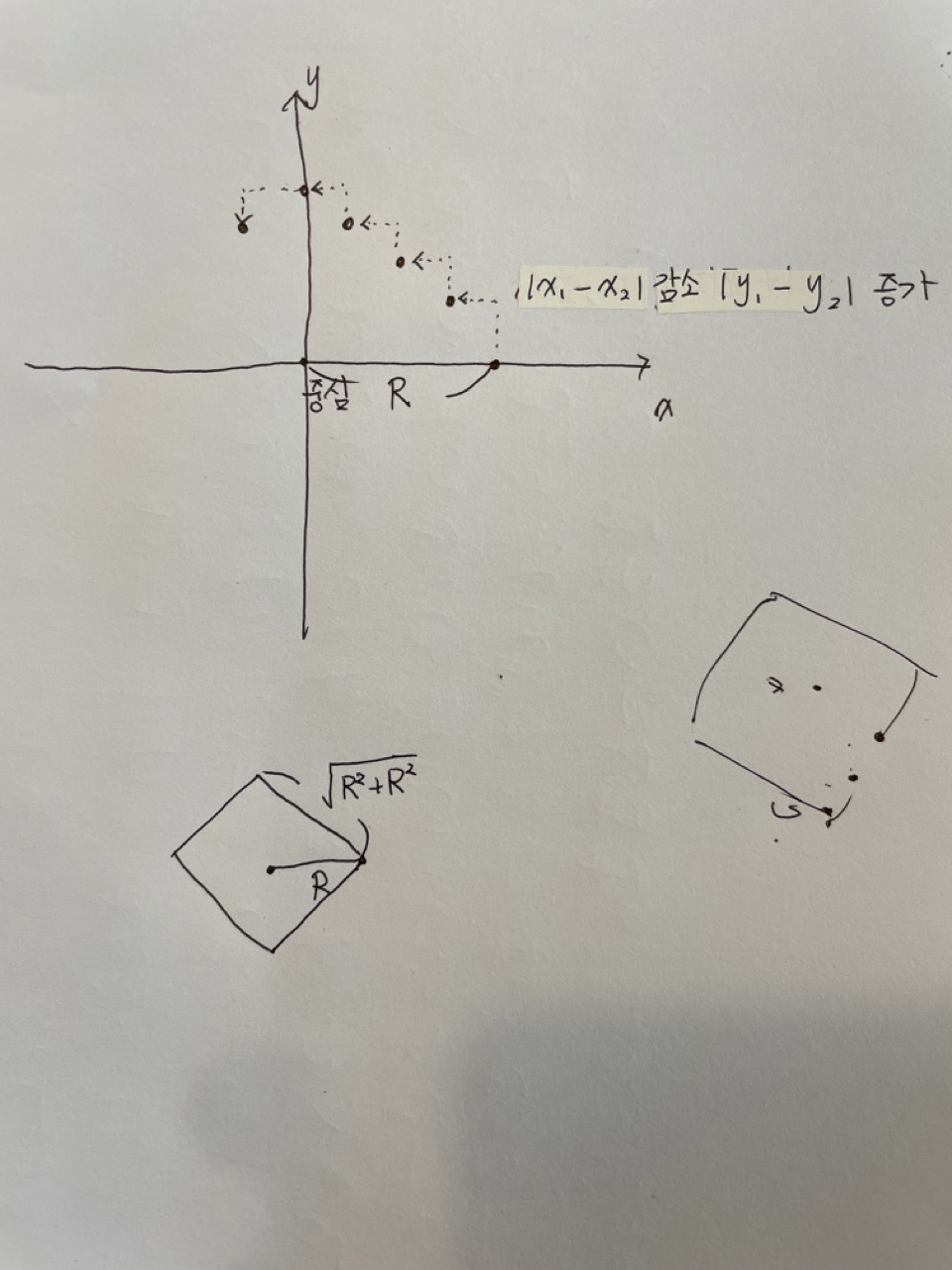
   1. 먼저 T1을 원점에 두고 T2는 x축 위에 R만큼 떨어진 점이라고 합시다.
   2. 택시 기하학에서 원의 정의는 유클리드 기하학과 동일하므로 동일한 거리만큼 떨어진 점들을 구해야 합니다.
   3. 거리를 구하는 공식은 D(T1,T2) = |x1-x2| + |y1-y2|이므로 |x1-x2|이 감소할 때 |y1-y2|가 증가해야 D(T1,T2)가 동일할 수 있게 됩니다.
   4. 따라서 이 원리를 따라서 |x1-x2|을 1씩 감소시키고 |y1-y2|를 1씩 증가시키면 아래와 같은 점들을 얻을 수 있습니다.
   5. 1사분면 외에 다른 사분면 들도 같은 똑같은 원리로 점들을 얻을 수 있습니다.
   6. 이렇게 점들을 찍어보면 택시기하학에서 반지름이 R인 원은 한변이 root(R^2 + R^2)인 정사각형임을 알 수 있습니다.