코딩테스트 연습 - 가장 큰 정사각형 찾기

문제 풀이 아이디어

🚫 Brutal Force

맨 처음에 문제를 풀 때는 row, column의 최댓값이 1,000 정도이므로 아래와 같은 코드로 정사각형을 최대 크기부터 하나하나 찾으면서 푸는 방법을 사용했는데요. 정확성 테스트는 통과할 수 있었지만 효율성 테스트는 하나도 통과할 수 없었습니다.

그도 그런 것이 아래 코드의 시간 복잡도는 O(N^3)이기 때문입니다. 물론 최대한 빠르게 실행되기 위해서 정사각형의 크기를 작은 것이 아니라 최댓값부터 찾았기 때문에 보통의 케이스들을 통과할 수 있었지만 효율성 테스트의 케이스는 통과할 수 없었던 것입니다.

func solution(_ board:[[Int]]) -> Int {
    let rowLength = board.count
    let columnLength = board[0].count
    let maxSize = min(rowLength, columnLength)

    func findSquare(_ r: Int, _ c: Int, _ size: Int) -> Bool {
        guard r + size <= rowLength && c + size <= columnLength else { return false }

        for i in r..<(r + size) {
            for j in c..<(c + size) {
                if board[i][j] == 0 { return false }
            }
        }

        return true
    }

    for size in stride(from: maxSize, to: 0, by: -1) {
        for r in 0..<rowLength {
            for c in 0..<columnLength {
                if findSquare(r, c, size) { return size * size }
            }
        }
    }

    return 0
}

👍 Dynamic Programming

O(N^3)의 알고리즘을 O(N^2)까지 줄여야 합니다. 즉 board에서 이중반복문 단 1개만 사용해야 하는 것이죠. 이 문제는 DP를 사용해서 현재의 node가 정사각형의 우하단에 위치한 꼭지점일 때 구할 수 있는 정사각형의 최대 크기를 board에 저장해가면서 문제를 풀어야 합니다.

DP의 원리

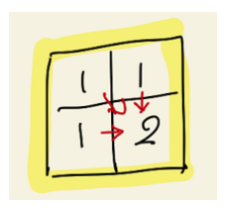
위 그림을 참고해서 설명해보도록 하겠습니다. (아이패드를 산 기념으로 직접 그림을 그려봤습니다.) 위 그림의 경우 우하단에 있는 칸 기준으로 좌상단, 상단, 좌측 3개의 위치에 모두 1이 존재하므로 해당 칸이 “정사각형의 우하단에 위치한 꼭지점”일 때 해당 정사각형의 최대 크기는 2입니다.

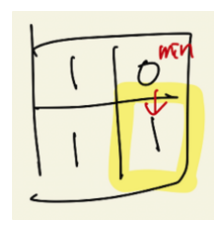
반면에 이런 케이스의 경우 좌상단, 좌측은 1이 존재하지만 상단에 0이 존재하므로 해당 칸이 “정사각형의 우하단에 위치한 꼭지점”일 때 해당 정사각형의 최대 크기는 1입니다.

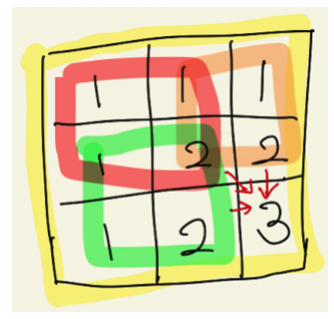
케이스를 한칸 더 키워서 보겠습니다. 위 케이스의 가장 오른쪽 하단 구석에 있는 칸을 기준으로 보았을 때 좌상단, 상단, 좌측이 모두 크기가 2인 정사각형을 만들 수 있습니다. 따라서 해당 칸에 1이 존재하는 경우, 해당 칸이 “정사각형의 우하단에 위치한 꼭지점”일 때 해당 정사각형의 최대크기는 3이 됩니다.

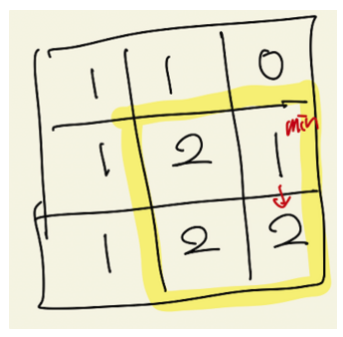
마지막 케이스입니다. 이번에는 좌상단, 좌측을 기준으로는 모두 크기가 2인 정사격형을 만들 수 있지만 상단을 기준으로는 크기가 1인 정사각형 밖에 만들 수 없습니다. 이 경우 해당 칸은 최대 크기가 2인 정사각형 밖에 만들 수 없게 됩니다.

점화식

위 원리를 통해서 우리는 아래와 같은 점화식을 도출할 수 있습니다.

if dp[r][c] != 0 {
    dp[r][c] = min(dp[r - 1][c - 1], dp[r][c - 1], dp[r - 1][c]) + 1
}

board의 크기가 1 * 1인 경우

아래 코드를 보시면 board의 크기가 1 * 1인 경우 반복문이 실행되지 않습니다. 이 경우를 대비해서 처음에 maxSize 값을 dp[0][0]으로 설정했습니다.

코드

func solution(_ board:[[Int]]) -> Int {
    // dp로 쓰기 위해 변수로 복사
    var dp = board
    // 사이즈 최대값
        //👉 board의 사이즈가 1 * 1인 경우 아래 반복문이 실행되지 않으므로 초기값을 dp[0][0]으로 해야 함!
    var maxSize = dp[0][0]
    
    for r in 1..<dp.count {
        for c in 1..<dp[0].count {
            // 현재 위치가 0이 아닌 경우 (= 정사각형이 될 수 있는 경우)
            if dp[r][c] != 0 {
                // 현재위치가 우하단 꼭지점인 정사각형의 최대 크기를 찾는다.
                dp[r][c] = min(dp[r - 1][c - 1], dp[r][c - 1], dp[r - 1][c]) + 1
                maxSize = max(maxSize, dp[r][c])
            }
        }
    }
    
    // 최대 "크기"를 리턴한다.
    return maxSize * maxSize
}