문제 링크

이진 트리 순회

정의

문제에 나온 순회의 방식은 전위 순회와 후위 순회입니다. 이 외에도 2가지 더 있는데요. 각각의 정의를 설명드리겠습니다.

1. 전위 순회: 루트 우선 (루트를 다 방문하고 나서 다른 노드로)
2. 후위 순회: 하위 트리 우선 (하위 트리를 다 방문하고 나서 루트로)
3. 중위 순회: 왼쪽 하위 트리를 방문하고 나서 루트로
4. 층별 순회: 각각의 층 별로 순회

문제에 주어진 트리를 각각의 방식으로 순회하면 아래와 같습니다.

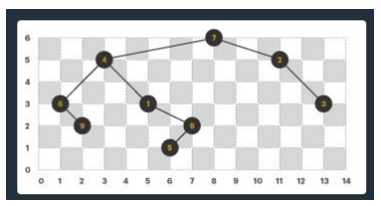
• 전위 순회 : 7, 4, 6, 9, 1, 8, 5, 2, 3
• 후위 순회 : 9, 6, 5, 8, 1, 4, 3, 2, 7
• 중위 순회: 6, 9, 4, 1, 5, 8, 7, 2, 3
• 층별 순회: 7, 4, 2, 6, 1, 3, 9, 8, 5

코드

해당 순회를 Swift 코드로 구현해봅시다. 먼저 이진 트리의 node를 class로 구현합니다. left와 right는 각각 왼쪽 자식 node, 오른쪽 자식 node를 의미합니다.

참고로 Node는 class로 만들어야 합니다. 할당할 경우 값이 복사되는 struct는 값 타입이기 때문에 내부에 또 다른 Node 객체를 property로 가질 수 없습니다.

class Node {
    var left: Node?
    var right: Node?
}

전위 순회를 코드로 구현하면 아래와 같습니다. 루트 노드를 먼저 순회하고 왼쪽 자식 노드로 가서 재귀적으로 전위 순회를 합니다. 왼쪽 자식이 모든 노드를 순회하면 오른쪽 자식으로 갑니다

var ans = [Node]()

func preOrder(now: Node?) {
    guard let now = now else { return }
    ans.append(now) //👉 루트 노드를 먼저 순회하고
    preOrder(now: now.left) //👉 왼쪽 자식 순회
    preOrder(now: now.right) // 
}

다음 후위 순회를 코드로 구현하면 아래와 같습니다. 먼저 왼쪽 자식의 하위 node를 모두 방문하고 오른쪽 자식의 하위 node를 모두 방문한 후에 루트를 순회합니다.

func postOrder(now: Node?) {
    guard let now = now else { return }
    postOrder(now: now.left)
    postOrder(now: now.right)
    ans.append(now)
}

다음은 중위 순회입니다. 코드가 비슷비슷합니다. 왼쪽 자식 노드를 다 순회한 후에 루트를 순회합니다. 그리고 오른쪽 노드를 순회합니다.

func inOrder(now: Node?) {
    guard let now = now else { return }
    inOrder(now: now.left)
    ans.append(now)
    inOrder(now: now.right)
}

마지막으로 층별 순회입니다. 재귀함수를 이용한 지금까지의 방식과는 다르게 큐를 사용해야 합니다. 자식 node가 아니라 같은 층이 기준이 되기 때문입니다. dfs와 bfs의 차이를 생각하시면 이해하기 편할 것 같네요.

func levelOrder(now: Node?) {
    var q = Queue<Node>()
    q.push(now)
    
    while !q.isEmpty {
        let now = q.pop()!
        ans.append(now)
        if let left = now.left {
            q.push(left)
        }
        if let right = now.right {
            q.push(right)
        }
    }
}

문제 풀이 아이디어

지금까지 이진 트리의 순회에 대해서 배워봤습니다. 이제 순회하는 방법을 알았으니 문제를 반 정도는 푼 것이나 다름 없습니다. 이제 해야할 일은 주어진 좌표를 Node로 만들고 Node들을 연결하여 이진 트리를 만드는 것입니다.

문제의 조건에 따르면 y 좌표가 클수록 높은 층위의 node이며, x좌표가 작을 수록 왼쪽 node입니다. 따라서 node를 층위 순으로 정렬하려면 y좌표의 내림차순으로 정렬하면 됩니다.

위 조건으로 정렬된 Node의 배열을 가지고 left와 right에 각각 자식 노드를 연결하는 함수를 아래와 같이 만들겠습니다. 자세한 설명은 주석을 참고해주세요.

// nodes는 y 기준 내림차순으로 정렬되어 있는 Node들의 배열
func makeTree(nodes: [Node]) {
    // 탈출 조건: 남은 nodes의 갯수가 없거나 1개 = 더 이상 연결할 자식 node가 없음
    if nodes.count < 2 { return }
    
    // 현재 nodes에서 root = y좌표가 가장 큰 node
    let root = nodes[0]
    
    // 각각 root의 왼쪽, 오른쪽 자식
    var lefts = [Node]()
    var rights = [Node]()
    
    // x 값을 기준으로 왼쪽 자식들과 오른쪽 자식들을 분리
        // nodes가 y 기준 내림차순이므로 lefts와 rights도 당연히 y기준으로 정렬되어 있음
    for i in 1..<nodes.count {
        if nodes[i].x < root.x {
            lefts.append(nodes[i])
        } else {
            rights.append(nodes[i])
        }
    }
    
    // 왼쪽 자식들에서 가장 y값이 높은 것이 left (없으면 nil)
    root.left = lefts.first
    // 오른쪽 자식들에서 가장 y값이 높은 것이 right (없으면 nil)
    root.right = rights.first
    
    // 양쪽 node들로 다시 tree 만들기
    makeTree(nodes: lefts)
    makeTree(nodes: rights)
}

코드

이제 트리와 순회 함수들이 완성되었으니 조합해서 문제를 풀면 됩니다. 전체 문제 풀이 코드는 아래와 같습니다.

class Node {
    let index: Int
    let x: Int
    let y: Int
    var left: Node?
    var right: Node?
    
    init(index: Int, x: Int, y: Int) {
        self.index = index
        self.x = x
        self.y = y
    }
}

// nodes는 y 기준 내림차순으로 정렬되어 있는 Node들의 배열
func makeTree(nodes: [Node]) {
    // 탈출 조건: 남은 nodes의 갯수가 없거나 1개 = 더 이상 연결할 자식 node가 없음
    if nodes.count < 2 { return }
    
    // 현재 nodes에서 root = y좌표가 가장 큰 node
    let root = nodes[0]
    
    // 각각 root의 왼쪽, 오른쪽 자식
    var lefts = [Node]()
    var rights = [Node]()
    
    // x 값을 기준으로 왼쪽 자식들과 오른쪽 자식들을 분리
        // nodes가 y 기준 내림차순이므로 lefts와 rights도 당연히 y기준으로 정렬되어 있음
    for i in 1..<nodes.count {
        if nodes[i].x < root.x {
            lefts.append(nodes[i])
        } else {
            rights.append(nodes[i])
        }
    }
    
    // 왼쪽 자식들에서 가장 y값이 높은 것이 left (없으면 nil)
    root.left = lefts.first
    // 오른쪽 자식들에서 가장 y값이 높은 것이 right (없으면 nil)
    root.right = rights.first
    
    // 양쪽 node들로 다시 tree 만들기
    makeTree(nodes: lefts)
    makeTree(nodes: rights)
}

func solution(_ nodeinfo:[[Int]]) -> [[Int]] {
    
    func preOrder(now: Node?) {
        guard let now = now else { return }
        preAns.append(now)
        preOrder(now: now.left)
        preOrder(now: now.right)
    }

    func postOrder(now: Node?) {
        guard let now = now else { return }
        postOrder(now: now.left)
        postOrder(now: now.right)
        postAns.append(now)
    }
    
    var nodes = [Node]()
    
    for i in 0..<nodeinfo.count {
        nodes.append(Node(index: i + 1, x: nodeinfo[i][0], y: nodeinfo[i][1]))
    }
    
    // y축 기준 내림차순 정렬
    nodes.sort { $0.y > $1.y }
    
    makeTree(nodes: nodes)
    
    // 각각 전위, 후위 순회 실시
    var preAns = [Node]()
    var postAns = [Node]()
    
    preOrder(now: nodes[0])
    postOrder(now: nodes[0])
    
    // 인덱스로만 바꾸어서 출력
    return [
        preAns.map { $0.index },
        postAns.map { $0.index }
    ]
}