코딩테스트 연습 - 멀쩡한 사각형

문제 풀이 아이디어

❗️w, h는 1억 이하의 자연수

처음에 이 문제를 봤을 때는 Dynamic Programming을 생각했습니다만, w와 h가 최대 1억이라는 것은 동적계획법으로 풀 경우 1억 1억의 엄청나게 큰 Cache가 필요하다는 의미입니다. 시간복잡도도 O(w h)라면 곤란하겠지요.

따라서 이 문제의 풀이법은 w와 h를 사용해서 바로 답을 구할 수 있는 공식을 찾아야 합니다.

최대공약수

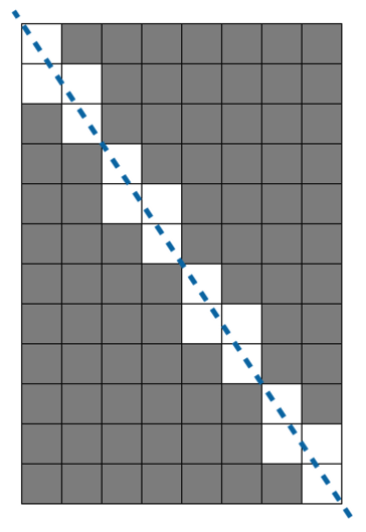
자 그렇다면 규칙성을 찾아야 합니다. 주어진 예시를 보도록 하겠습니다. w가 8, h가 12인 사각형입니다. 선을 그어진 사각형을 보면 같은 패턴이 4번 반복되는 것을 볼 수 있습니다. 바로 w가 2, h가 3인 사각형이 4번 반복되는 형태입니다.

즉 w(= 8)과 h(= 12)의 최대공약수를 g(= 4)라고 할 때 w/g(= 2), h/g (= 3)인 사각형이 g번 반복되는 패턴입니다.

사각형 세기

자 이제 w, h가 커도 최대공약수를 통해서 작은 사각형으로 나누어서 구할 수 있게 되었습니다. 그렇다면 각각의 단위 사각형에서 몇 개의 버려지는 사각형이 나오는지 구해야 합니다.

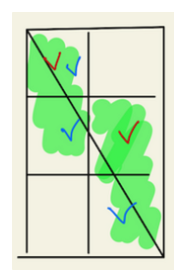
w, h를 각각 g로 나눈 값을 w’와 h’라고 합시다. w’와 h’는 서로소 관계입니다. 아래 예시를 봐주세요.

먼저 w’가 2, h’가 3인 사각형입니다. 가로 기준으로 보았을 때 (빨간 체크) w’개의 사각형이 있습니다. 세로 기준 (파란 체크)으로 보면 h’개의 사각형이 있습니다. 다만 1개의 사각형이 겹치므로 1을 빼주어야 합니다. w’ + h’ - 1입니다.

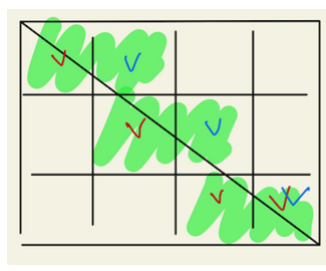
다른 예시로 위 공식을 검증해보도록 하겠습니다. w’가 4, h’가 3인 사각형입니다. 마찬가지로 빨간 체크 w’개, 파란 체크 h’개 겹치는 것 1개입니다.

최종 공식

우리가 구하는 것은 멀쩡한 사각형이므로 전체 사각형에서 위 공식을 통해서 구한 못 쓰는 사각형을 빼주어야 합니다. 즉 w h - g (w’ + h’ - 1)입니다. 그런데 w’ g = w, h’ g = h이므로 정리하면 w * h - (w + h - g)가 되겠습니다. 이제 코드로 옮기기만 하면 됩니다.

다 정리하고 나니까 수학문제에 가깝네요. 아래 코드에서는 재귀함수를 통해서 최대공약수를 구하는 방법만 주목해서 보시면 되겠습니다.

코드

func solution(_ w:Int, _ h:Int) -> Int64 {

    // 최대공약수 구하는 함수: 유클리드 호제법
    func gcd(_ a: Int, _ b: Int) -> Int {
        if b == 0 {
            return a
        } else {
            return gcd(b, a % b)
        }
    }

    return Int64(w * h - (w + h - gcd(w, h)))
}