문제 풀이 아이디어
트리?
해당 구조물은 트리로 되어 있습니다. 따라서 자연스럽게 class로 Node를 만들고 일단 트리 자료구조를 만들어 놓고 문제를 풀기 시작하는 분들 계실 것 같습니다. (저도 그랬습니다;;;) 하지만 일반적은 DFS로 풀 수 있는 문제입니다.
DFS
늑대와 양의 위치가 일정한 규칙이 있는 것이 아니기 때문에 완전탐색을 사용하는 방법 밖에는 없습니다. DFS를 실시하기 위해서는 탐색할 수 있는 다음 node와 탈출조건을 알아야 합니다.
1. 다음으로 방문할 수 있는 node는?
문제의 조건에 따르면 한번 방문한 node를 다시 방문해도 괜찮습니다. 최단거리 문제가 아니라 최대한 양을 많이 모으는 것이 목표이니까요.
따라서 다음에 방문할 수 있는 node는 자기 자식 node 뿐만이 아닙니다. 트리를 거슬러 올라가서 이미 방문한 다른 node들의 자식 node들도 방문할 수 있습니다. 아래 그림을 보겠습니다.
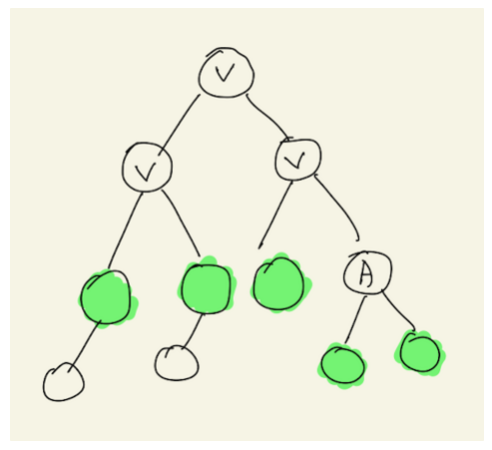
V 표시가 된 곳은 이미 방문한 node입니다. 그리고 A node가 현재 방문 중인 node입니다. 해당 node에서 다음으로 탐색할 수 있는 node는 A의 자식 node들 말고도 이미 방문한 node들 중에 아직 방문하지 않은 자식 node들도 있습니다. 즉, 초록색으로 표시된 node들을 다음 node로 탐색할 수 있다는 것이죠.
초록색으로 표시된 node들을 정의하면 부모 node는 방문했지만 아직 자식 node는 방문하지 않은 경우의 자식 node들입니다.
2. 탈출 조건
다음은 탈출 조건입니다. 보통 DFS를 할 때는 현재 탐색하는 정답에 도달한 경우 return을 하는 경우가 많은데요. 이 문제의 경우는 반대입니다.
늑대의 수가 양보다 많거나 같아지면 정답이 아닙니다. 그리고 해당 node에서 다른 node로 추가적인 탐색을 하는 것도 불가능합니다. 따라서 return합니다.
반면에 양의 수가 늑대보다 많다면 추가적인 탐색이 가능합니다. 따라서 다른 node를 더 탐색해야 합니다. 하지만 추가적인 탐색을 하고 return이 될 수도 있습니다. 그렇게 되면 정답을 저장할 기회가 없을 것입니다.
따라서 추가적인 탐색을 하기 전에 현재까지 모은 양의 갯수를 저장합니다. 그리고 저장한 값 중에서 가장 큰 값을 리턴하면 됩니다.
시간복잡도
DFS의 시간복잡도는 노드의 갯수를 N, 간선의 갯수를 E라고 했을 때 O(N + E)입니다. N이 최대 17이고 트리의 구조이므로 E도 그리 크지 않습니다. 따라서 시간초과를 걱정할 필요가 없습니다.
코드
func solution(_ info:[Int], _ edges:[[Int]]) -> Int {
// 방문 배열과 정답배열
var visited = Array(repeating: false, count: info.count)
var ans = [Int]()
// dfs
func dfs(sheep: Int, wolf: Int) {
// 정답 조건에 만족하면 저장
if sheep > wolf {
ans.append(sheep)
// 불만족하면 리턴
} else {
return
}
// 모든 간선을 순회하면서
for edge in edges {
let parent = edge[0], child = edge[1]
// 부모는 방문했고 자식은 방문하지 않은 edge를 찾는다.
// 부모는 이미 방문했으므로 현재 node에서 갈 수 있다. (돌아서라도)
if visited[parent] && !visited[child] {
visited[child] = true
if info[child] == 0 {
dfs(sheep: sheep + 1, wolf: wolf)
} else {
dfs(sheep: sheep, wolf: wolf + 1)
}
visited[child] = false
}
}
}
visited[0] = true
dfs(sheep: 1, wolf: 0)
return ans.max()!
}