참고한 블로그 🙏

스위프트 | "(최소)힙 구현"하기 (Swift5 | Heap - MinHeap)

Swift) 힙(Heap) 구현 해보기

힙의 정의

최댓값 혹은 최솟값의 연산을 빠르게 하기 위해서 고안된 완전이진트리를 기반으로 한 자료구조를 의미합니다.

힙의 이진트리는 부모 node가 자식 node보다 더 작은 (혹은 큰) 구조를 유지하고 있습니다. 새로운 데이터가 들어 올 때 이 원칙으로 트리를 다시 정렬하고 데이터가 나갈 때도 마찬가지입니다.

간단하게 이야기하면 힙은 안에 데이터를 넣기만 하면 자동으로 정렬을 해주는 자료구조라고 볼 수 있습니다. 시간 복잡도는 O(logn)입니다.

힙의 원리

insert

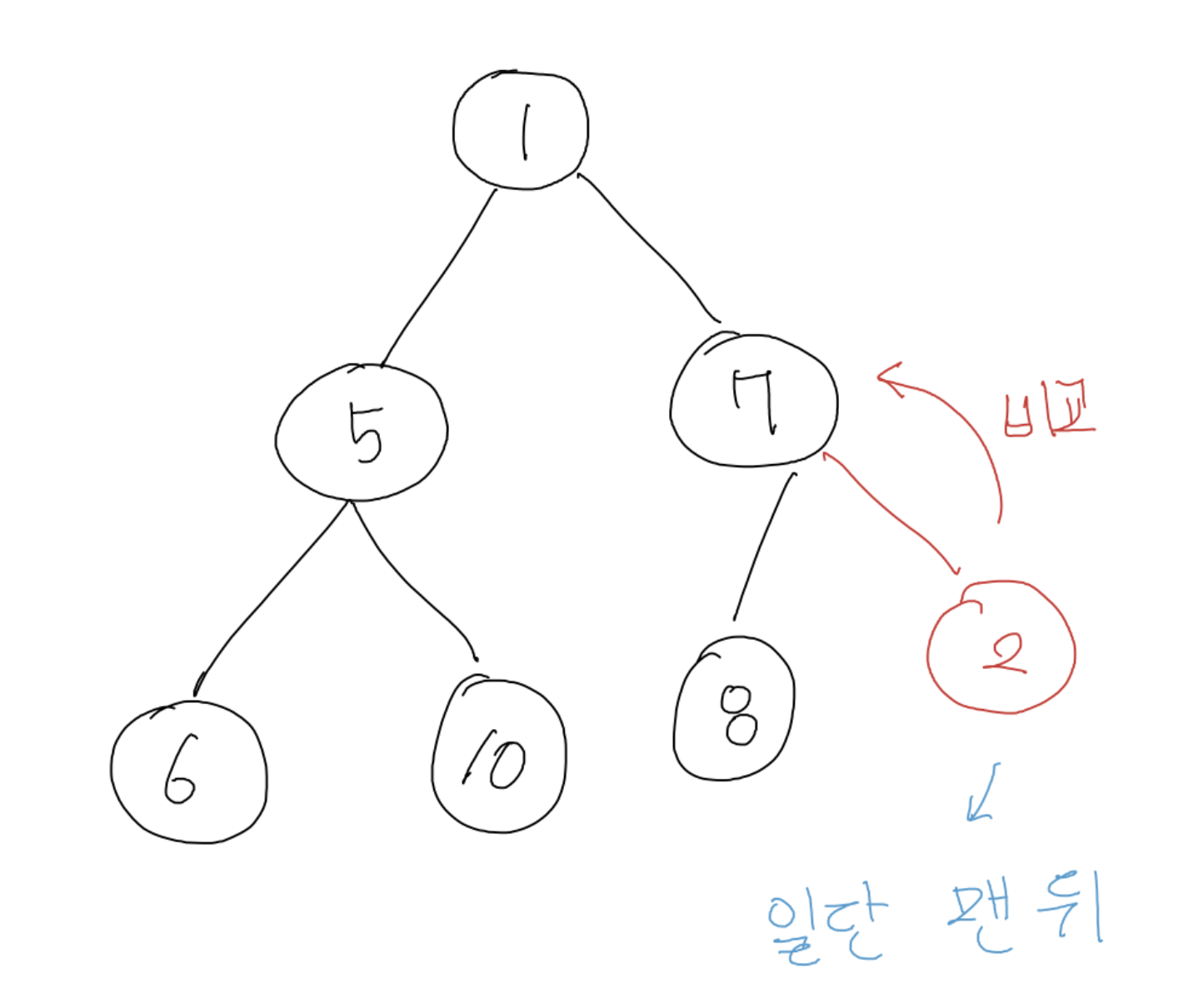
새로운 데이터를 insert할 때는 일단 힙의 맨 아래에 insert합니다. 그 이후에 부모 node와의 비교를 통해 부모 node보다 작으면 위로 올라가고 부모 node보다 크면 그대로 있는 방식으로 제자리를 찾아갑니다.

mutating func insert(_ element: T) {
    //✅ 빈 heap이라면 init과 똑같은 동작
    if heap.isEmpty {
        heap.append(element)
        heap.append(element)
        return
    }
    
    //✅ 일단 맨 뒤에 넣고
    heap.append(element)
    
    //✅ 부모 node와 비교해서 올라갈지 여부를 결정하는 함수
    func isMoveUp(_ insertIndex: Int) -> Bool {
        if insertIndex <= 1 { //❓ 맨 위 (root node까지 올라왔을 때)
            return false //❗️ 더 이상 올라갈 때 없으므로 false
        }
        
        let parentIndex = insertIndex / 2 //👉 부모 node의 index (짝수, 홀수 관계 없이 Int니까 반올림)
        return heap[insertIndex] < heap[parentIndex] ? true : false //👉 부모 node와 값 비교
    }
    
    var insertIndex = heap.count - 1 //👉 가장 마지막 node의 index
    
    //✅ 부모 node와 비교하면서 제자리를 찾아간다.
    while isMoveUp(insertIndex) {
        let parentIndex = insertIndex / 2
        heap.swapAt(insertIndex, parentIndex) //👉 시간 복잡도 O(1)
        insertIndex = parentIndex //👉 부모 node와 자리 바꾸었으므로 insertIndex 갱신
    }
}

pop

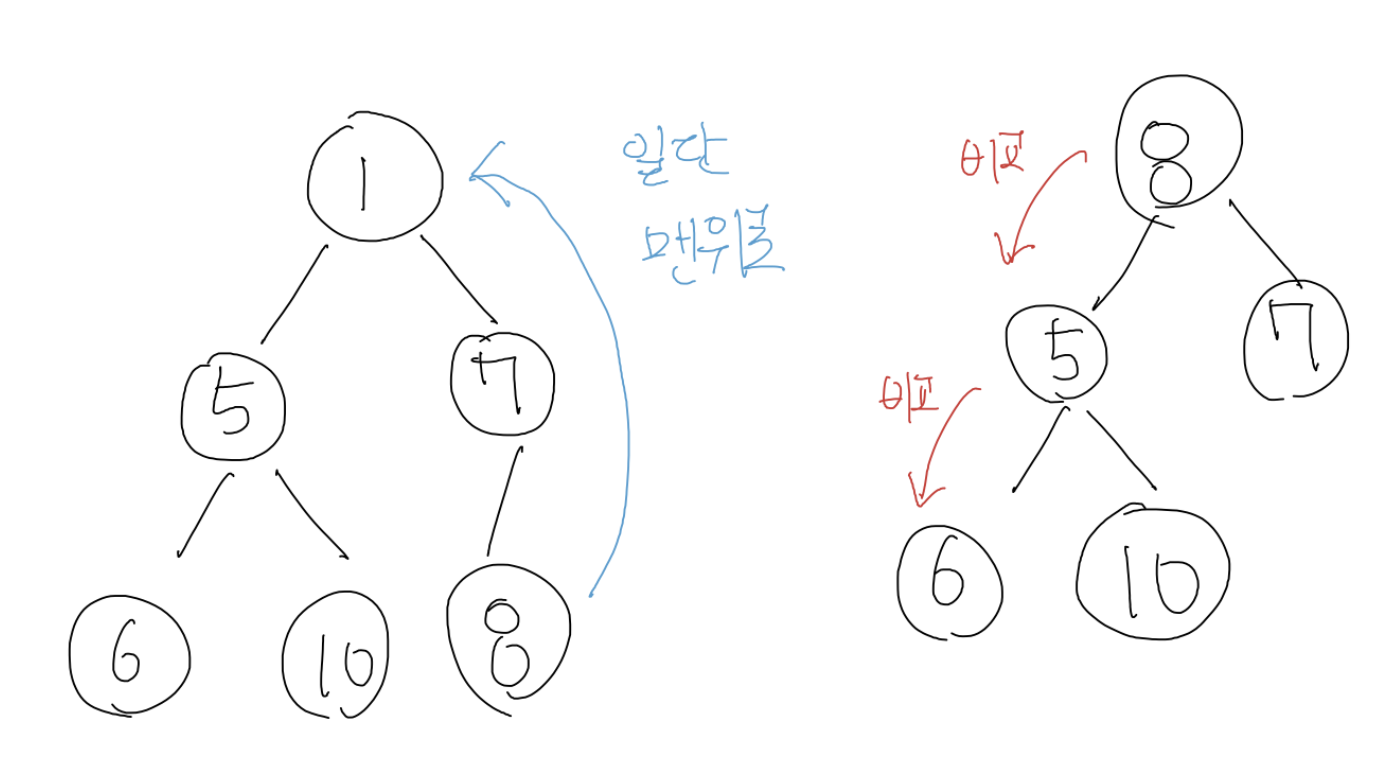
일단 pop할 node (이진 트리의 가장 상위에 위치한 데이터)를 가장 마지막 node와 바꾸고 pop합니다. 가장 상위 node를 자식 node들과 비교해 하면서 제자리를 찾아갑니다.

//✅ 어느 자식 node와 자리를 바꿀지
enum moveDownDirection { case left, right, none }

//✅ 자료 빼기
    //👉 일단 맨 위로 올리고 제자리 찾아가기
mutating func pop() -> T? {
    //✅ heap이 비었을 때
    if heap.count <= 1 {
        return nil
    }
    
    //✅ root node에 있는 자료를 리턴
    let returnData = heap[1]
    heap.swapAt(1, heap.count - 1) //👉 root node 맨 뒤로 보내고
    heap.removeLast() //👉 pop하기
    
    //✅ root node와 자리를 바꾼 맨 마지막 node의 원래 자리를 찾아주기 위한 함수
    func moveDown(_ poppedIndex: Int) -> moveDownDirection {
        //✅ 자식 node들의 index
        let leftChildIndex = poppedIndex * 2 //👉 왼쪽은 2배
        let rightChildIndex = leftChildIndex + 1 //👉 오른쪽은 2배 + 1
        
        //1️⃣ 자식 node가 없는 경우 (왼쪽 자식만 확인하면 됨)
        if leftChildIndex >= heap.count {
            return .none //👉 더 이상 내려갈 곳이 없다. (제자리)
        }
        
        //2️⃣ 왼쪽 자식 node만 있는 경우
        if rightChildIndex >= heap.count {
            return heap[leftChildIndex] < heap[poppedIndex] ? .left : .none
            //👉 왼쪽 자식 node와 비교해서 내가 더 크면 왼쪽과 swap
        }
        
        //3️⃣ 자식 node가 둘 다 있다.
        //3️⃣ - 1 : 모든 자식 node들이 나보다 큰 경우
        if (heap[leftChildIndex] > heap[poppedIndex]) && (heap[rightChildIndex] > heap[poppedIndex]) {
            return .none //👉 swap할 필요가 없음
        }
        
        //3️⃣ - 2 : 모든 자식 node들이 나보다 작은 경우
        if (heap[leftChildIndex] < heap[poppedIndex]) && (heap[rightChildIndex] < heap[poppedIndex]) {
            return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
            //👉 두 자식 node 중에서 더 작은 쪽과 swap (작은 쪽이 부모로 올라가야 하니까)
        }
        
        //3️⃣ - 3 : 둘 중에 하나만 나보다 작은 경우
        if (heap[leftChildIndex] < heap[poppedIndex]) || (heap[rightChildIndex] < heap[poppedIndex]) {
            return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
            //👉 작은 쪽과 swap
        }
        
        return .none
    }
    
    //✅ heap 맨 위에서 제자리를 찾아가는 과정
    var poppedIndex = 1
    while true {
        switch moveDown(poppedIndex) {
        case .none:
            return returnData
        case .left:
            let leftChildIndex = poppedIndex * 2
            heap.swapAt(poppedIndex, leftChildIndex)
            poppedIndex = leftChildIndex
        case .right:
            let rightChildIndex = (poppedIndex * 2) + 1
            heap.swapAt(poppedIndex, rightChildIndex)
            poppedIndex = rightChildIndex
        }
    }
}

힙의 구현

🤔  index를 왜 1부터 시작할까? → 0부터 시작하게 되면 자식 node를 구할 때 예외처리를 해주어야 함. (0은 2배를 해도 0이므로)

// 최소힙 구현
import Foundation

struct MinHeap<T: Comparable> {
    var heap: [T] = []

    var isEmpty: Bool {
        return heap.count <= 1 ? true : false
    }
    
    
    init() {}
    // 첫 node를 가지고 init할 때
    init(_ element: T) {
        heap.append(element) //👉 0번 index 일부러 채우기 (아니면 예외처리 해야함)
        heap.append(element) //👉 1번 index가 root node
    }
    
    //✅ 자료 넣기
        // 👉 일단 자료에 넣고서 부모 node와 비교해가면서 위로 올린다.
    mutating func insert(_ element: T) {
        //✅ 빈 heap이라면 init과 똑같은 동작
        if heap.isEmpty {
            heap.append(element)
            heap.append(element)
            return
        }
        
        //✅ 일단 맨 뒤에 넣고
        heap.append(element)
        
        //✅ 부모 node와 비교해서 올라갈지 여부를 결정하는 함수
        func isMoveUp(_ insertIndex: Int) -> Bool {
            if insertIndex <= 1 { //❓ 맨 위 (root node까지 올라왔을 때)
                return false //❗️ 더 이상 올라갈 때 없으므로 false
            }
            
            let parentIndex = insertIndex / 2 //👉 부모 node의 index (짝수, 홀수 관계 없이 Int니까 반올림)
            return heap[insertIndex] < heap[parentIndex] ? true : false //👉 부모 node와 값 비교
        }
        
        var insertIndex = heap.count - 1 //👉 가장 마지막 node의 index
        
        //✅ 부모 node와 비교하면서 제자리를 찾아간다.
        while isMoveUp(insertIndex) {
            let parentIndex = insertIndex / 2
            heap.swapAt(insertIndex, parentIndex) //👉 시간 복잡도 O(1)
            insertIndex = parentIndex //👉 부모 node와 자리 바꾸었으므로 insertIndex 갱신
        }
    }
    
	//✅ 어느 자식 node와 자리를 바꿀지
    enum moveDownDirection { case left, right, none }
    
    //✅ 자료 빼기
        //👉 일단 맨 위로 올리고 제자리 찾아가기
    mutating func pop() -> T? {
        //✅ heap이 비었을 때
        if heap.count <= 1 {
            return nil
        }
        
        //✅ root node에 있는 자료를 리턴
        let returnData = heap[1]
        heap.swapAt(1, heap.count - 1) //👉 root node 맨 뒤로 보내고
        heap.removeLast() //👉 pop하기
        
        //✅ root node와 자리를 바꾼 맨 마지막 node의 원래 자리를 찾아주기 위한 함수
        func moveDown(_ poppedIndex: Int) -> moveDownDirection {
            //✅ 자식 node들의 index
            let leftChildIndex = poppedIndex * 2 //👉 왼쪽은 2배
            let rightChildIndex = leftChildIndex + 1 //👉 오른쪽은 2배 + 1
            
            //1️⃣ 자식 node가 없는 경우 (왼쪽 자식만 확인하면 됨)
            if leftChildIndex >= heap.count {
                return .none //👉 더 이상 내려갈 곳이 없다. (제자리)
            }
            
            //2️⃣ 왼쪽 자식 node만 있는 경우
            if rightChildIndex >= heap.count {
                return heap[leftChildIndex] < heap[poppedIndex] ? .left : .none
                //👉 왼쪽 자식 node와 비교해서 내가 더 크면 왼쪽과 swap
            }
            
            //3️⃣ 자식 node가 둘 다 있다.
            //3️⃣ - 1 : 모든 자식 node들이 나보다 큰 경우
            if (heap[leftChildIndex] > heap[poppedIndex]) && (heap[rightChildIndex] > heap[poppedIndex]) {
                return .none //👉 swap할 필요가 없음
            }
            
            //3️⃣ - 2 : 모든 자식 node들이 나보다 작은 경우
            if (heap[leftChildIndex] < heap[poppedIndex]) && (heap[rightChildIndex] < heap[poppedIndex]) {
                return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
                //👉 두 자식 node 중에서 더 작은 쪽과 swap (작은 쪽이 부모로 올라가야 하니까)
            }
            
            //3️⃣ - 3 : 둘 중에 하나만 나보다 작은 경우
            if (heap[leftChildIndex] < heap[poppedIndex]) || (heap[rightChildIndex] < heap[poppedIndex]) {
                return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
                //👉 작은 쪽과 swap
            }
            
            return .none
        }
        
        //✅ heap 맨 위에서 제자리를 찾아가는 과정
        var poppedIndex = 1
        while true {
            switch moveDown(poppedIndex) {
            case .none:
                return returnData
            case .left:
                let leftChildIndex = poppedIndex * 2
                heap.swapAt(poppedIndex, leftChildIndex)
                poppedIndex = leftChildIndex
            case .right:
                let rightChildIndex = (poppedIndex * 2) + 1
                heap.swapAt(poppedIndex, rightChildIndex)
                poppedIndex = rightChildIndex
            }
        }
    }
}

주석 제거 버전

// 최소힙 구현
import Foundation

struct MinHeap<T: Comparable> {
    var heap: [T] = []

    var isEmpty: Bool {
        return heap.count <= 1 ? true : false
    }
    
    
    init() {}

    init(_ element: T) {
        heap.append(element)
        heap.append(element)
    }
    
    mutating func insert(_ element: T) {
        if heap.isEmpty {
            heap.append(element)
            heap.append(element)
            return
        }
        
        heap.append(element)
        
        func isMoveUp(_ insertIndex: Int) -> Bool {
            if insertIndex <= 1 {
                return false
            }
            
            let parentIndex = insertIndex / 2
            return heap[insertIndex] < heap[parentIndex] ? true : false
        }
        
        var insertIndex = heap.count - 1

        while isMoveUp(insertIndex) {
            let parentIndex = insertIndex / 2
            heap.swapAt(insertIndex, parentIndex)
            insertIndex = parentIndex
        }
    }
    
    enum moveDownDirection { case left, right, none }
    
    mutating func pop() -> T? {
        if heap.count <= 1 {
            return nil
        }
        
        let returnData = heap[1]
        heap.swapAt(1, heap.count - 1)
        heap.removeLast()
        
        func moveDown(_ poppedIndex: Int) -> moveDownDirection {
            let leftChildIndex = poppedIndex * 2
            let rightChildIndex = leftChildIndex + 1
            
            if leftChildIndex >= heap.count {
                return .none
            }
            
            if rightChildIndex >= heap.count {
                return heap[leftChildIndex] < heap[poppedIndex] ? .left : .none
            }
            
            if (heap[leftChildIndex] > heap[poppedIndex]) && (heap[rightChildIndex] > heap[poppedIndex]) {
                return .none
            }
            
            if (heap[leftChildIndex] < heap[poppedIndex]) && (heap[rightChildIndex] < heap[poppedIndex]) {
                return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
            }
            
            if (heap[leftChildIndex] < heap[poppedIndex]) || (heap[rightChildIndex] < heap[poppedIndex]) {
                return heap[leftChildIndex] < heap[rightChildIndex] ? .left : .right
            }
            
            return .none
        }
        
        var poppedIndex = 1
        while true {
            switch moveDown(poppedIndex) {
            case .none:
                return returnData
            case .left:
                let leftChildIndex = poppedIndex * 2
                heap.swapAt(poppedIndex, leftChildIndex)
                poppedIndex = leftChildIndex
            case .right:
                let rightChildIndex = (poppedIndex * 2) + 1
                heap.swapAt(poppedIndex, rightChildIndex)
                poppedIndex = rightChildIndex
            }
        }
    }
}