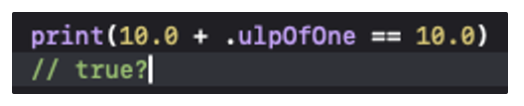
오늘은 Double, Float 등 소수점을 다루는 수에 정의된 .ulpOfOne이라는 개념에 대해서 알아본다.
정의
공식 문서를 보고 가자. 공식 문서에 따른 정의는 아래와 같다.
The positive difference between 1.0 and the next greater representable number.
해석을 해보면 1.0과 그 다음으로 큰 “표현할 수 있는” 수의 양적인 차이 (= 음수가 아니라 양수라는 이야기)라는 뜻이다. 여기서 주목할 점은 “표현할 수 있는”이라는 표현이다. (참고로 ulp는 Unit in the Last Piece이다.)
swift의 Float를 저장하기 위해서는 32비트, Double은 64비트의 메모리가 필요하다. 따라서 소수점을 무한대로 모두 표현할 수 있는 것은 아니다. 따라서 최대한 효과적으로 소수점을 표현하기 위해서 “IEEE Standard 754 Floating Point Numbers”라는 표준을 따른다. Floating Point는 우리말로는 부동 소수점이라고 하는데 간단히 설명하면 간단하게 설명할 수 밖에 없다. 실수를 표현할 때 소수점의 위치를 나타내는 지수와 유효 숫자를 표현하는 가수로 나누어서 표현하는 방식이다.
즉 (부호) / (가수부) / (기수) / (지수)로 표현한다. 뭔소리야 간단한 예를 들어보자.
1.2345을 표현하기 위해서 0 / 12345 / 10 / -4로 표현하는 식이다. 0은 양수라는 것을 의미한다. 12345는 가수부로 소수점을 제외하고 보이는 숫자만 양의 정수로 표현한다. 기수는 이 가수부에 곱할 수의 밑이다. 그리고 지수는 밑의 지수.
즉 1.2345 = (-1)^0 12345 10^(-4)로 표현하는 방식이다.
이 방법의 한가지 단점이 있다. 바로 “지수”가 차지하는 메모리가 커지면 “가수부”에 할당할 수 있는 메모리가 줄어든다는 점이다.
단순하게 설명
저걸 그대로 다 설명하는 것은 불가능하므로 아주 단순화해서 설명하겠다. 예를 들어 A라는 자료형은 4자리의 십진수와 소수점의 위치를 저장할 수 있다고 가정을 하자. 그렇다면 1.0은 “1.000”로 저장할 수 있을 것이다. 이 자료형에서 1.0 다음으로 큰 “표현할 수 있는” 1.0보다 큰 바로 “1.001”이다. 즉 ulpOfOne은 바로 “0.001”이 되는 것이다.
왜 “10.0 + .ulpOfOne == 10.0”은 true인가?
그럼 오늘의 메인 질문인 왜 “10.0 + .ulpOfOne == 10.0”은 true인가?”에 대한 답을 알아보자. 위에 A라는 자료형을 사용해서 10.0을 표현해보자. 4자리 십진수 밖에 못 쓰므로 “10.00”이 될 것이다. 여기에 A 자료형의 ulpOfOne인 “0.001”을 더하면 어떻게 될까?
현실에서는 “10.001”로 표현하면 되지만 A 자료형의 메모리로는 표현할 수 없는 숫자다. 다라서 “10.00” + “0.001”은 그냥 “10.00”이 된다. 따라서 “10.0 + .ulpOfOne == 10.0”은 true가 되는 것이다.
그렇다면 ulpOfTen은 없는가?
당연히 없다. 하지만 간접적으로 구할 수는 있다. 바로 10.0 (1 + .ulpOfOne)을 하는 것이다. 다시 A 자료형으로 예시를 들어보자. 표현할 수 있는 “10.00”보다 큰 다음 수는 “10.01”이다. “10.00” “1.001”을 연산한 값과 동일하다.
마치며: 나는 왜 .ulpOfOne을 알게 되었는가?
나는 10.0보다는 크고 100.0보다는 작은 수의 범위를 나타내기 위해서 아래 같은 코드를 작성했다.
(10.0 + .ulpOfOne)..<100.0이 포스팅을 끝까지 읽은 분들은 아마 저 위 코드가 얼마나 바보 같은지 알 것이다. 저 코드는 사실상 아래 코드와 같다.
10.0..<100.0의도한 대로 하려면 아래와 같이 작성해야 한다.
(10.0 * (1 + .ulpOfOne))..<100.0우연히 이런 과정을 통해서 오랜만에 열심히 찾아서 공부해본 것 같다. 요즘 CS를 다시 처음부터 공부하고 있는데 (포스팅도 할 생각이다. “리제로부터 시작하는 CS 공부”) 큰 도움이 된 것 같다.
