알고리즘
1.유클리드 호제법 (Euclidean Algorithm)

🦖 유클리드 호제법 두 개의 수가 주어졌을때, 최대공약수(GCD)를 구하는 알고리즘 두 개의 자연수 a와 b가 주어진다. a는 b보다 큰 자연수이며 a를 b로 나눈 나머지를 r이라고 하자. 이때 a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
2022년 6월 21일
2.에라토스테네스의 체

소수를 찾는 방식2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.2는 소수이므로 오른쪽으로 이동하고 자기자신을 제외한 2의 배수를 모두 지운다.남아있는 수 중에서 3은 소수이므로 오른쪽으로 이동하고 자기자신을 제외한 3의 배수를 모두 지운다.남아있는 수 중에서
2022년 6월 27일
3.탐욕법 (Greedy Algorithm)
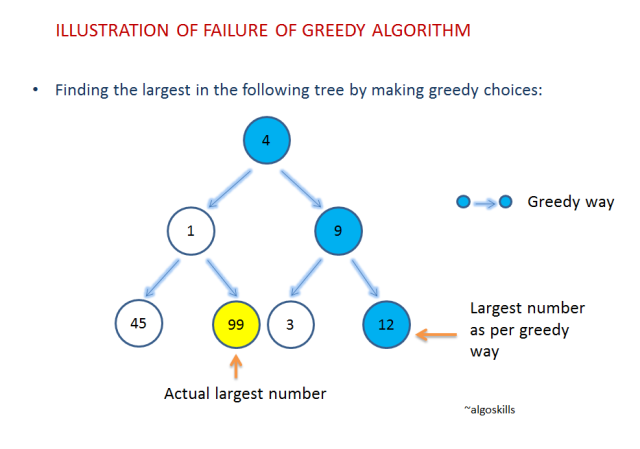
현재 상황에서 가장 좋은 것을 고르는 알고리즘문제를 해결하는 과정에서 그 순간마다 최적이라고 생각되는 결정을 하는 방식으로 최종 해답에 도달하는 방식이다.동적프로그래밍을 간단한 문제해결에 사용하면 지나치게 많은 일을 한다는 것을 착안하여 고안되었다.순간마다 하는 선택은
2022년 6월 30일
4.JAVA로 순열, 중복 순열, 조합, 중복 조합 이해하기

프로그래머스-소수만들기문제를 해결하면서 조합코드를 찾아보게 되었고 그 외에 순열과 중복이 가능한 경우에 대해서 공부가 필요하다고 생각되서 정리해보았다.순열에서는 순서가 중요하기 때문에 1,2 와 2,1은 순서가 다르므로 다른 경우의 수로 카운팅한다.순서가 있게 뽑는 것
2022년 7월 5일