From Cryptohack.org
- course 2 ( MODULAR ARITHMETIC ) -
2번째 과정은 cryptography 에서 매우 많이 쓰이는 modular 에 대한 과정인듯 하다. 첫번째 문제부터 살펴보자.
< 1 >
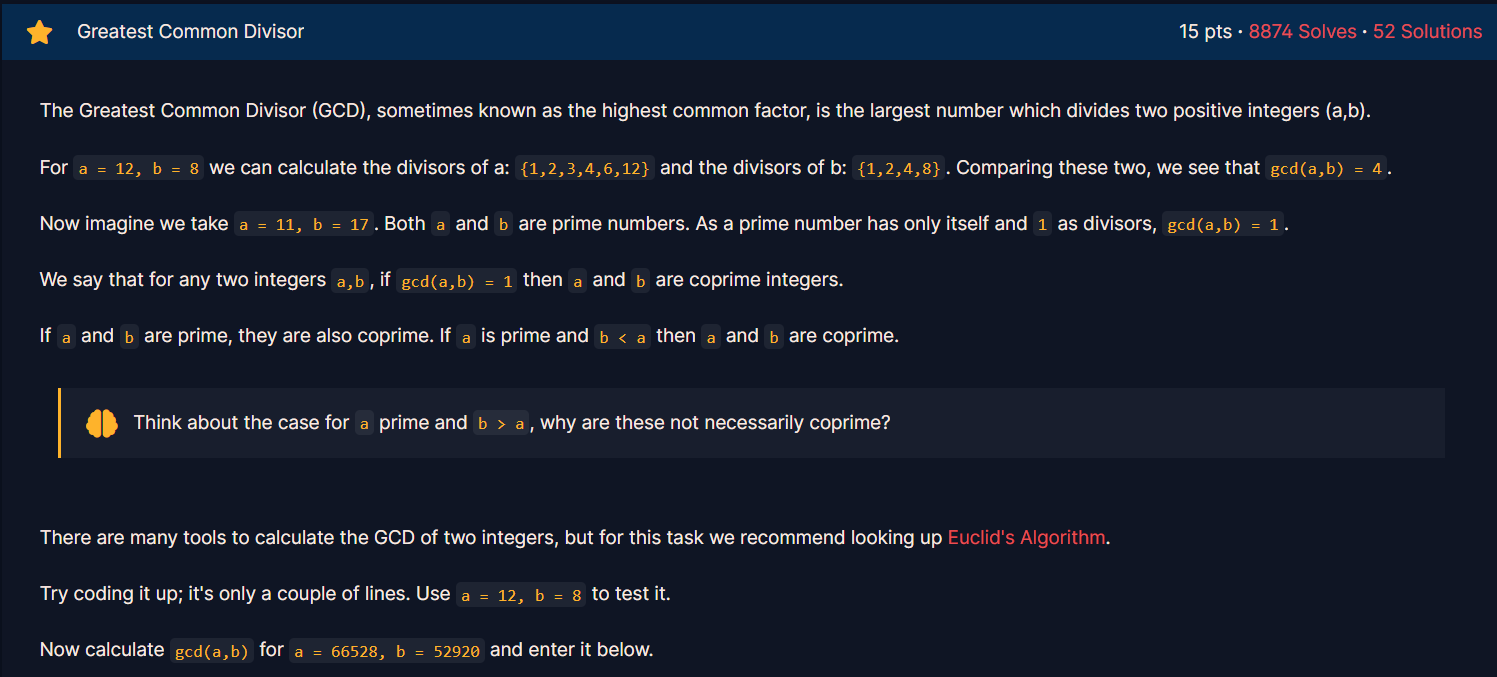
GCD 는 greateset common divisor 즉, 최대공약수의 약자이다. 앞선 내용은 GCD 에 대한 설명인듯 하고, 문제에 나와 있는 Euclid's Algorithm 을 이용해서 두 수의 GCD 를 구하라는 문제인 것 같다.
먼저, 유클리드 알고리즘에 대해서 잘 모르는 사람은 다음 페이지를 보고 오는 걸 추천한다.
이 알고리즘을 통해서 우리는 최대공약수를 구할 수 있다. 물론 python 에는 이 유클리드 알고리즘을 구현한 모듈이 있어 손쉽게 구할 수 있지만, 문제의 의도에 맞추어 스스로 구현해보도록 하자.
a = 66528
b = 52920
def Euclid(m,n):
if m == n:
return n
if m % n == 0:
return n
return Euclid(n, m % n)
print(Euclid(a,b))
이렇게 유클리드 호제법 함수를 만들 수 있겠다.
바로 실행해보자.
1512
< 2 >
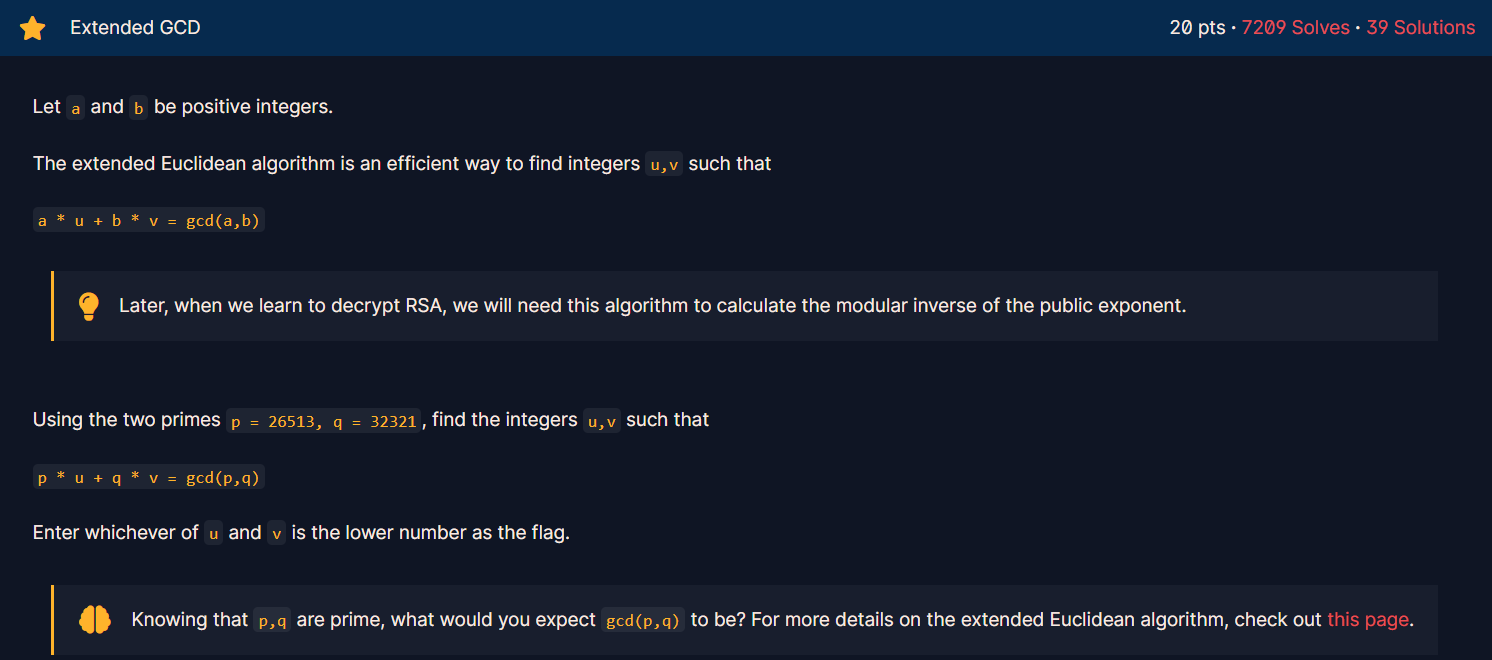
Extended GCD, GCD 의 확장버전이다. 두 수 p, q 에 대해서
p * u + q * v = gcd(p,q) 를 만족하는 u 와 v 를 찾는 것이 이 문제의 목표인 것 같다.
< 1 > 에서는 유클리드 알고리즘을, < 2 > 에서는 확장된 유클리드 알고리즘에 대해서 설명하고 있다.
확장된 유클리드 알고리즘에 대한 설명은 다음 링크에 있다.
- 확장된 유클리드 알고리즘은 위 사진에 명시된 것처럼, RSA 암호를 복호화하고, key 를 알아내는 데에 필수적인 요소라고 할 수 있다.
- 잘 이해가 가지 않는다면, 이렇게 생각해도 좋다. 우리는 유클리드 알고리즘에서 a 와 b 를 토대로 gcd( a, b )를 구하는 알고리즘을 작성했다.
- 하지만, 이 GCD 를 찾는 과정에서 우리는 나머지를 구하는 연산을 이용해서 나머지로만 계산을 했는데, 이제는 몫까지 계산함으로써 얼마나 빼야 GCD 가 만들어질지를 계산하는 것이다.
충분한 설명이 되었으리라 생각한다. 이제 코드를 작성해보자.
p = 26513
q = 32321
s = [1, 0]
t = [0, 1]
r = [p, q]
while True:
if r[-1] == 0:
print(f'u = {s[-2]} and v = {t[-2]}')
break
q = r[-2] // r[-1]
r.append(r[-2]-r[-1]*q)
t.append(t[-2]-t[-1]*q)
s.append(s[-2]-s[-1]*q)
이렇게 작성해줄 수 있겠다.
바로 실행해보자.
u = 10245 and v = -8404
< 3 >
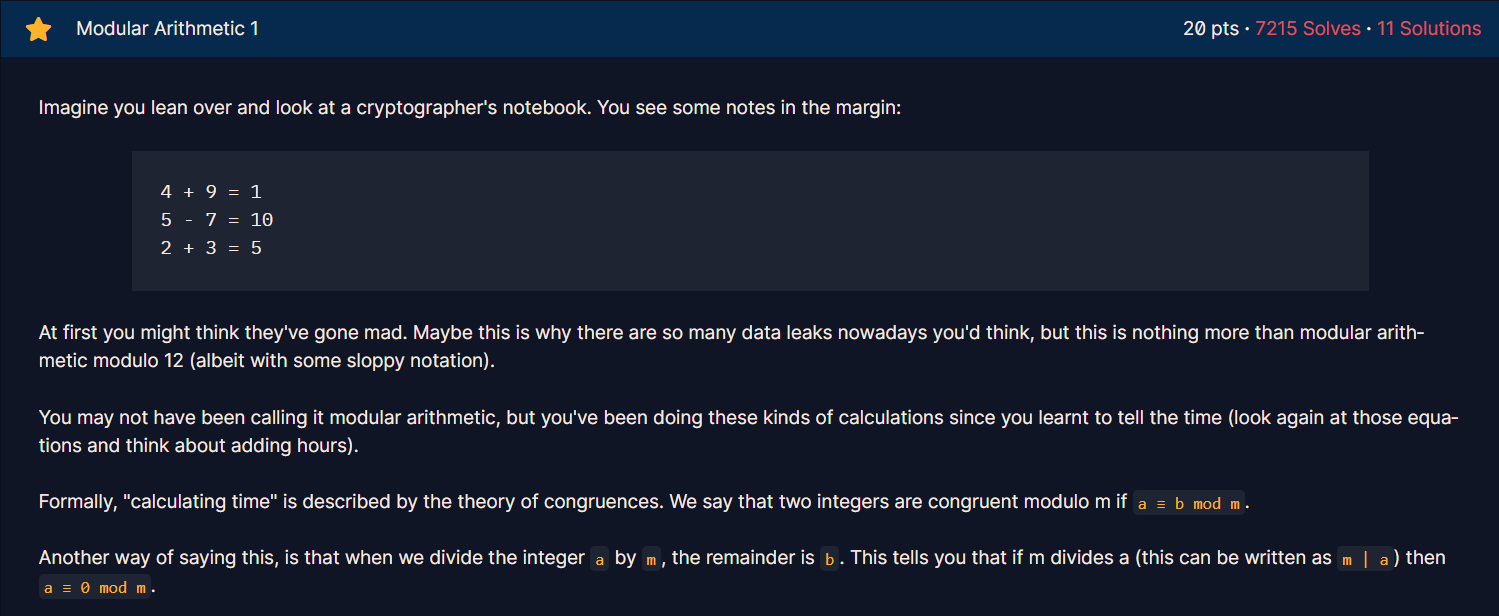
이제 본격적으로 modular 에 대한 과정이 시작되었다.
대부분 modular 이 어떤 연산 (?) 인지 알고 있을 걸로 예상되지만, 모르는 사람들을 위해 간단히 설명하자면, modular 은 나머지 연산과 같다고 생각해도 된다.
예시로 4 = 1 ( mod 3 ) 이라고 볼 수 있겠다.
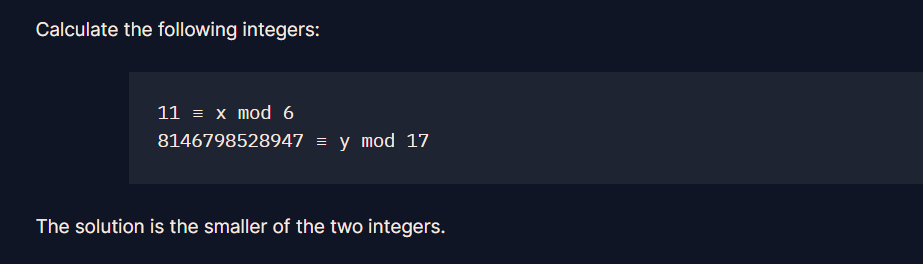
문제는 다음 x y 중에서 더 작은 값을 구하는 것 같다.
X 는 굳이 컴퓨터를 사용하지 않고도 빠르게 머릿속으로 계산할 수 있을 것 같다. X 는 알다시피 5 가 되겠다.
num = 8146798528947
print(num % 17)
굳이 코드까진 필요 없었지만 허전해서 넣었다.. ㅎㅎ
바로 실행해보면 4 가 나오게 된다.
따라서 더 작은 값은 4 가 되겠다.
< 4 >
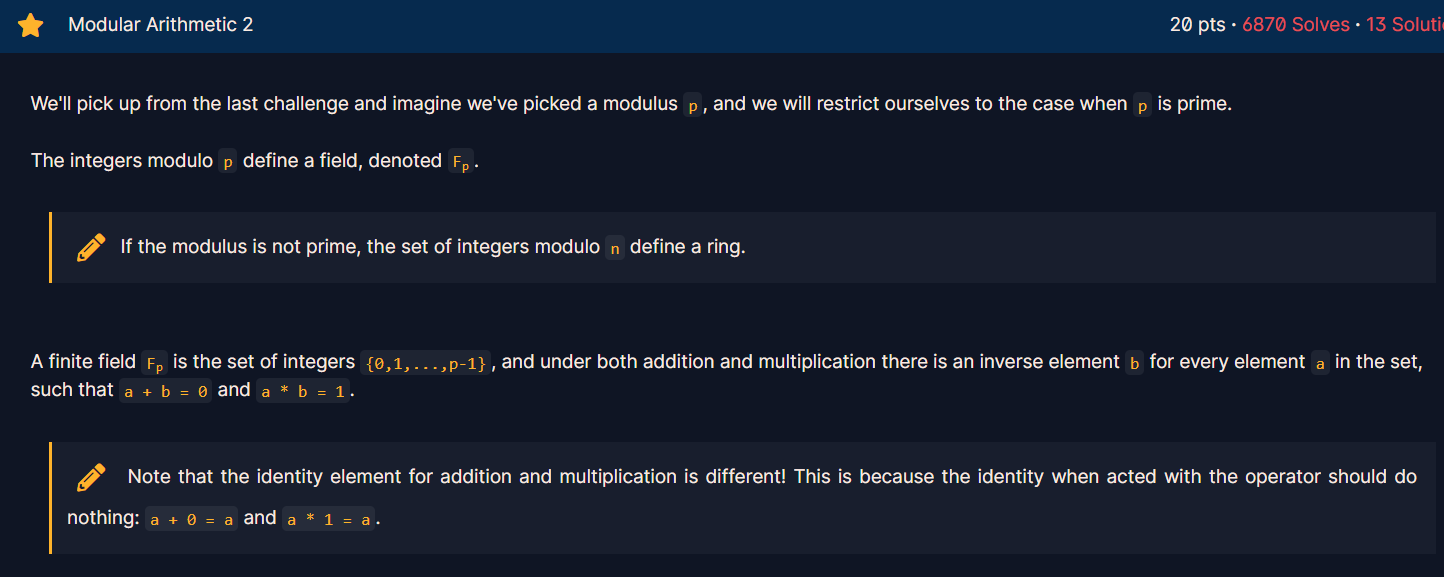
modular Prime에 대해서 modular 연산을 통한 값은
{0, 1, . . . , p-1} 총 p 개의 값만 가능하다. 이를 "군" 이라고 하는데, 이번 포스팅에서 설명하기에는 너무 방대한 개념이니 나중에 따로 포스팅하도록 하겠다.
여기서 주의깊게 보아야 할 점은 이 군 중에서 임의의 원소 A 를 정의하더라도, A + B = 0, A * C = 1 ( modular P ) 를 만족하는 B 와 C 가 항상 존재한다는 것이다.
( 여담이지만 이는 윌슨의 정리 와도 연관성이 있다. 수학에 관심있는 사람들은 꼭 한번쯤은 보길 추천한다. )
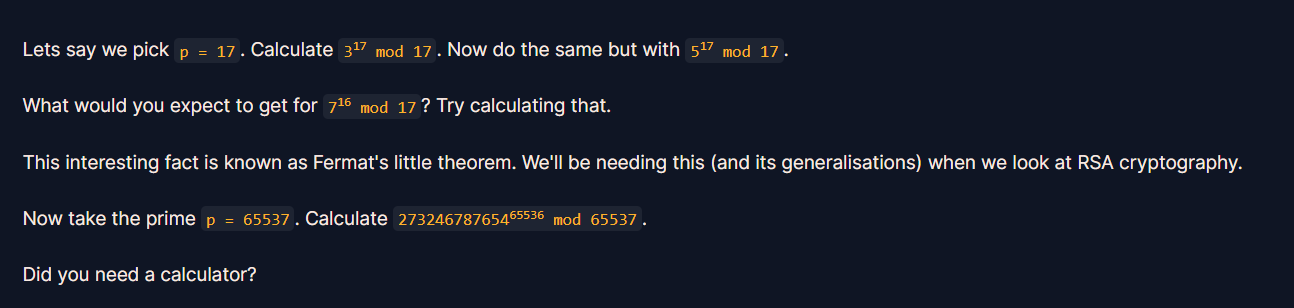
그래서 우리가 해결해야 할 문제는 다음과 같다.
27324678765465536 ^ 65536 = ??? ( mod 65537 )
앞선 말에서 힌트를 얻을 수 있다. 3 의 17제곱, 5의 17 제곱, 7의 16 제곱을 mod 17 에 대해서 계산해보면 한가지 규칙을 얻을 수 있다.
바로 a ^ 16 = 1 ( mod p ) 라는 것이다.
이를 페르마 소정리 라고 한다.. 역시 암호학은 공부할 것이 많다.. ( 아직 별 거 아니니 참고하시길.. )
따라서 우리는 굳이 python 으로 계산하지 않고도 답을 구할 수 있겠다.
정답은 1 이 되겠다.
< 5 >
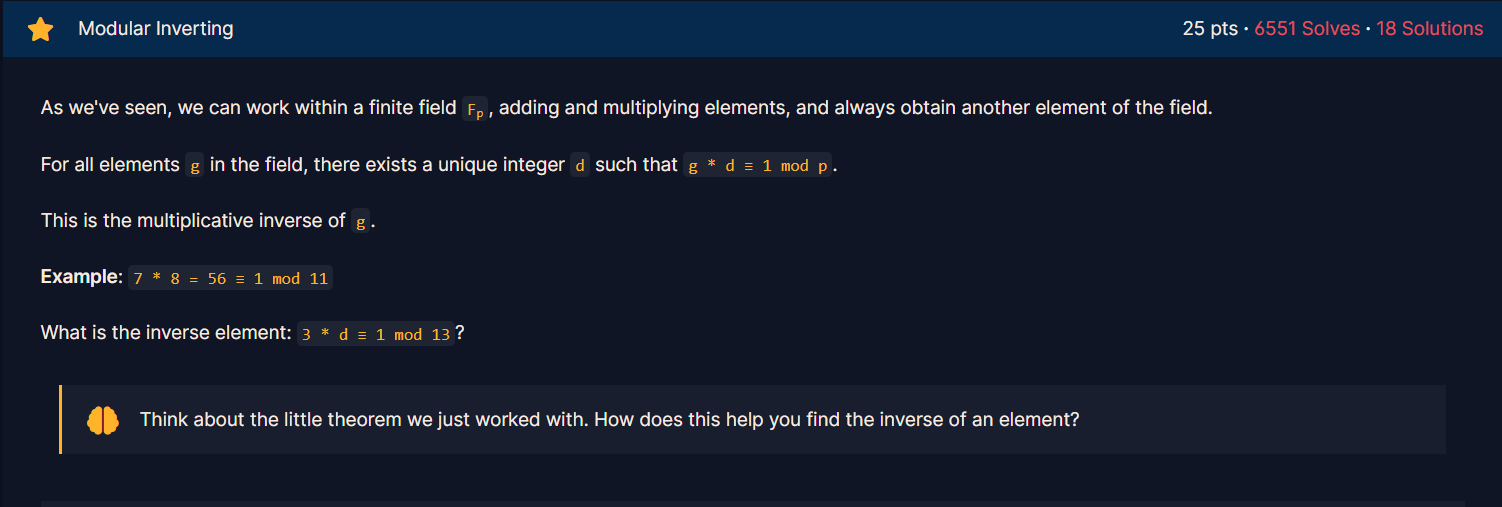
이번 문제도 군론의 일부이다. 앞서 말한 < 4 > 번 문제에서 말한 군론을 살짝 끌고오자면, 소수 P 에 대한 잉여계는 항상 곱셈에 대한 역원이 존재한다.. ( 이 정도 말은 알아들을 수 있어야 한다 ㅠㅠ )
따라서 임의의 수를 잡더라도, A * B = 1 ( mod P ) 를 만족하는 B 가 존재하는데, 이 B 를 mod P 에서 A 의 역수, 역원이라고 보통 이야기한다.
python 에는 너무너무 고맙게도 이를 계산해주는 모듈이 있다. 이번에는 이 모듈을 사용해서 코드를 짜보도록 하자.
from Crypto.Util.number import inverse
print(inverse(3,13))
바로 실행해보자.
결과는 9 가 나왔다. 검산해보면 3 * 9 = 27 = 13 * 2 + 1
따라서 3 * 9 = 1 ( mod 13 ) 이라고 볼 수 있겠다.
벌써 course 2 의 절반 정도까지 도달했다.
다음 포스팅은 이어서 본격적으로 정수론의 꽃, 2차 잉여계부터 시작해보도록 하자.
공부할 내용은 무궁무진하니 많이 많이 공부해보자...