백준 1389: 케빈 베이컨의 6단계 법칙 (플로이드 워셜)

챌린저 문제를 앞에서부터 풀어보려고 한다.

챌린저 Day2
백준 1389: 케빈 베이컨의 6단계 법칙

그래프의 모든 노드 간의 거리를 구해야 하기 때문에 처음에는 DFS로 풀려고 했는데 잘 안돼서 질문 게시판을 보니 플로이드 워셜 알고리즘을 쓴다고 한다.

• 플로이드 워셜: 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구하는 알고리즘

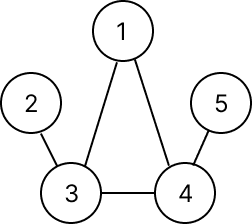
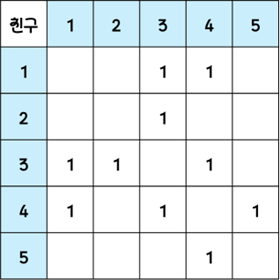
1. 친구 관계 그래프, 테이블

문제에 나온 친구 관계를 그래프, 테이블로 나타냄
모든 거리는 1

2. 최단거리 테이블
   

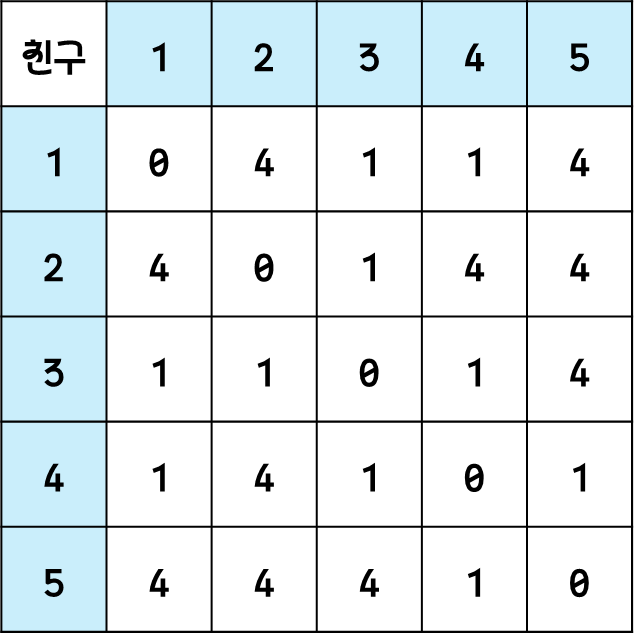
자기자신과의 거리: 0
간선이 없는 노드 사이의 거리: 모두 친구 관계로 이어져있기 때문에 가장 먼 친구와의 거리는 n-1단계인 4

3. a↔b의 거리
   a와 b는 다른 친구 m들을 거치면 무조건 이어져 있다
   모든 m을 거쳐보면서 최소 몇 단계인지 확인한다
   d[a][b]= d[a][b]와 d[a][m] + d[m][b] 중 최소

4. 모든 a의 케빈 베이컨 수를 구한 후 가장 작은 a의 인덱스를 출력

5. 구현

n, m = map(int, input().split())
d = [[n - 1] * n for _ in range(n)]
for i in range(n):
    d[i][i] = 0

for _ in range(m):
    a, b = map(int, input().split())
    d[a - 1][b - 1] = 1
    d[b - 1][a - 1] = 1

for m in range(n):
    for a in range(n):
        for b in range(n):
            d[a][b] = min(d[a][b], d[a][m] + d[m][b])
            d[b][a] = d[a][b]

kevin = list(sum(d[i]) for i in range(n))
print(kevin.index(min(kevin)) + 1)