자료구조를 공부함에 따라 자연스레 시간 복잡도와 공간 복잡도의 개념에 대해서도 공부하게 되었다. 자료구조의 종류는 다양하고 각 자료구조마다 장단점이 존재하므로 개발자는 자신이 원하는 자료구조를 사용할 수 있어야 한다. 모든 경우에서 항상 우월한 성능을 보이는 자료구조와 알고리즘은 없으므로 끊임없는 공부가 필요할 것 같다.
알고리즘의 성능분석의 주된 요소는 시간 복잡도(Time Complexity), 공간 복잡도(Space Complexity) 두가지로 볼 수 있다. 이 포스트에서는 시간 복잡도에 대해 알아보려고 한다.
시간복잡도(Time Complexity)
시간 복잡도는 입력 값의 개수와 알고리즘의 처리 시간과의 상관관계를 표현한 것이다. 입력 데이터의 양이 많아지짐에 따른 처리 속도를 표현한다. x를 데이터로 하고 y를 시간으로 했을때 x(데이터)가 증가함에 따라 y(시간)의 변화를 나타내게 된다.
▶︎ Big-O
-
O(1) => Constant Time
입력 데이터의 크기와 상관없이 언제나 일정한 시간이 걸리는 알고리즘이다. 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다. -
O(log n) => Log Time
Binary search tree access(이진검색), -search(검색), -insertion(삽입), -deletion(삭제)
데이터 양이 많아져도 시간은 조금씩 늘어난다. 시간에 비례하여 탐색 가능한 데이터의 양은 2의 n승이 된다. 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다. -
O(n) => linear Time
for문을 통한 탐색을 생각하면 되는데, 데이터의 양에 따라 시간이 정비례한다. -
O(n^2) => Quadratic Time
데이터의 양에 따라 시간은 제곱에 비례한다. 문제를 해결하기 위한 단계의 수가 입력값 n의 제곱이기에 상당히 효율이 좋지 않은 시간 복잡도이다.
위 그림은 Big-O 표기법에 따른 시간 복잡도의 표시 방법이다. Better에 가까울 때 성능이 좋다고 볼 수 있다. 이 외에도 점근 표기법이라고 해서 빅오(Big-O), 빅오메가(big-Ω),빅세타(big-Θ) 표기법이 있다.
하지만 왜 우리는 Big-O 표기법을 사용하는지 알아야 한다. 그 이유는 알고리즘 효율성을 상한선 기준으로 표기하기 때문이다. 쉽게 말하자면 가장 최악의 상황을 가정하는 것이다. 이에 반해 빅오메가는 최선의 상황을 가르키며 하한선을 기준으로 표기하고 빅세타는 빅오와 빅오메가의 평균을 나타낸다고 이해하면 된다.
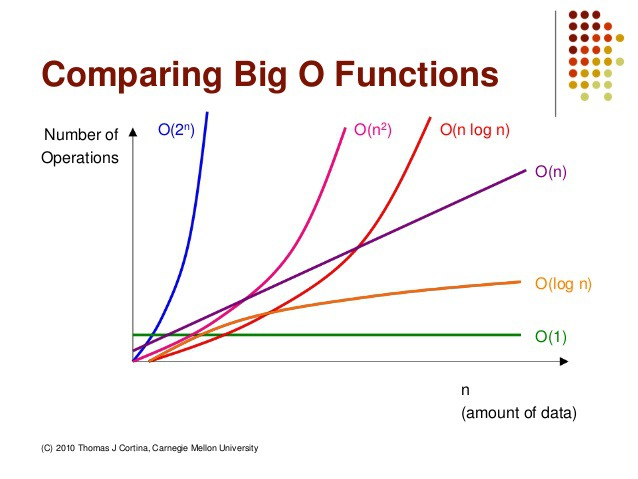
시간 복잡도의 성능 비교
상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수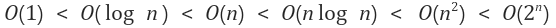
▶︎ Big-O 표기법의 특징
-
상수항 무시
빅오 표기법은 데이터 입력값(n)이 충분히 크다고 가정하고, 알고리즘의 효율성이 데이터 입력값의 크기에 따라 영향 받기에 상수항 같은 사소한 부분은 무시한다.
-
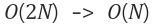
영향력 없는 항 무시
데이터 입력값(n)의 크기에 따라 영향을 받기 때문에 가장 영향력이 큰 항 이외의 영향력이 없는 항들은 무시한다.(차수가 가장 높은 최고차항만 둔다)
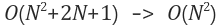
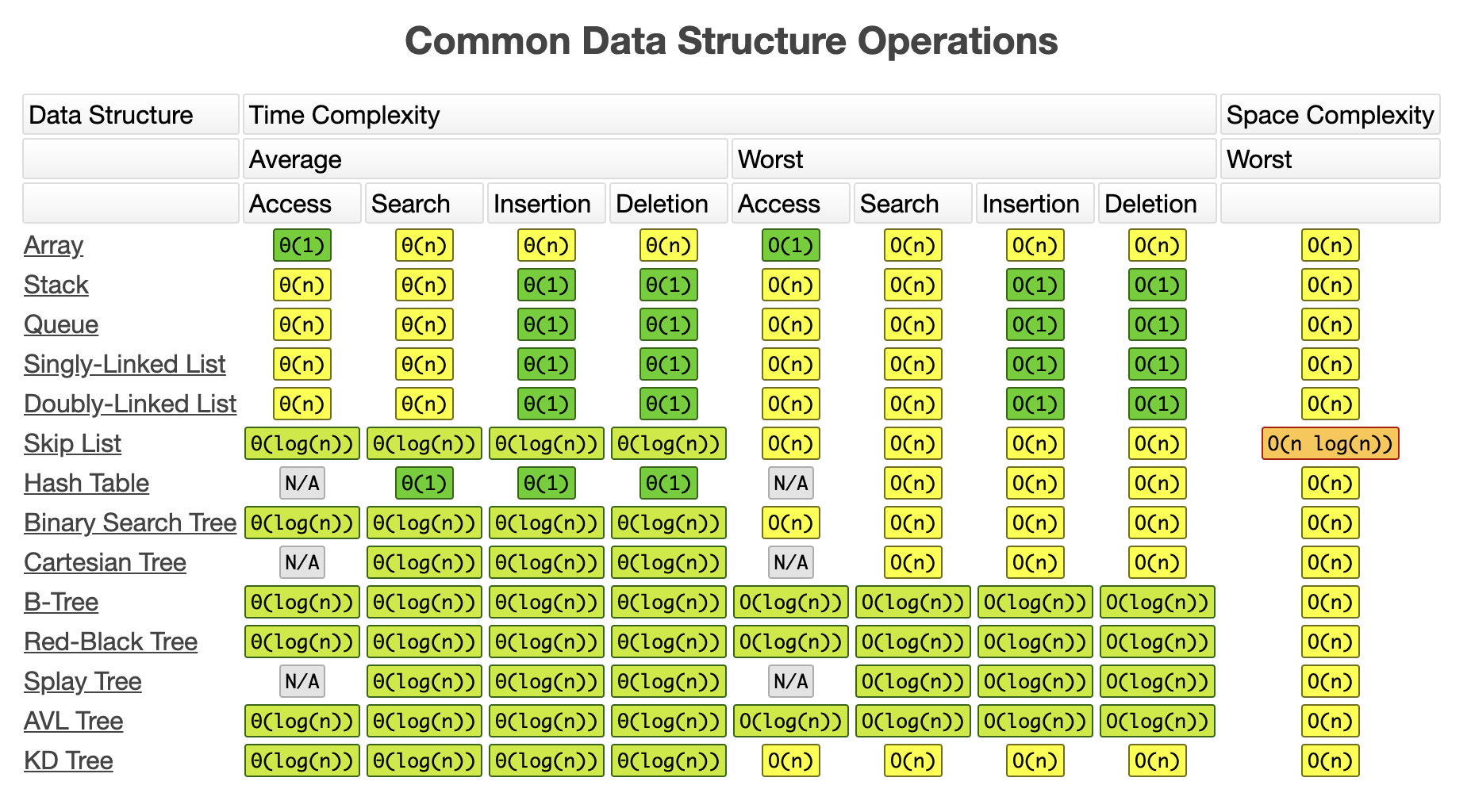
굉장히 수학적인 개념이라 가볍게 넘어가고 싶지만 효율적인 자료구조와 알고리즘을 구현하기 위해 계속해서 공부해야겠다.
