_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.png)
탐욕법(그리디) 알고리즘이란?
탐욕법(이하 '그리디') 알고리즘이란 현재 상황에서 가장 좋은 것(최선의 선택)을 고르는 알고리즘을 말합니다.
그리디 알고리즘은 동적 프로그래밍을 간단한 문제 해결에 사용하면 지나치게 많은 일을 한다는 것을 착안하여 고안되었습니다.
그리디 알고리즘은 현재 상황에서 가장 좋은 결과를 선택해나가는 방식입니다. 하지만 이 가장 좋은 결과는 최종적인 결과 도출에 대한 최적해를 보장해주는 것은 아닙니다!
여기서 가장 좋은 것(최선의 선택) 이란?
그리디 알고리즘이 추구하는 가장 좋은 것에 대해 예시를 들어 알아보겠습니다.
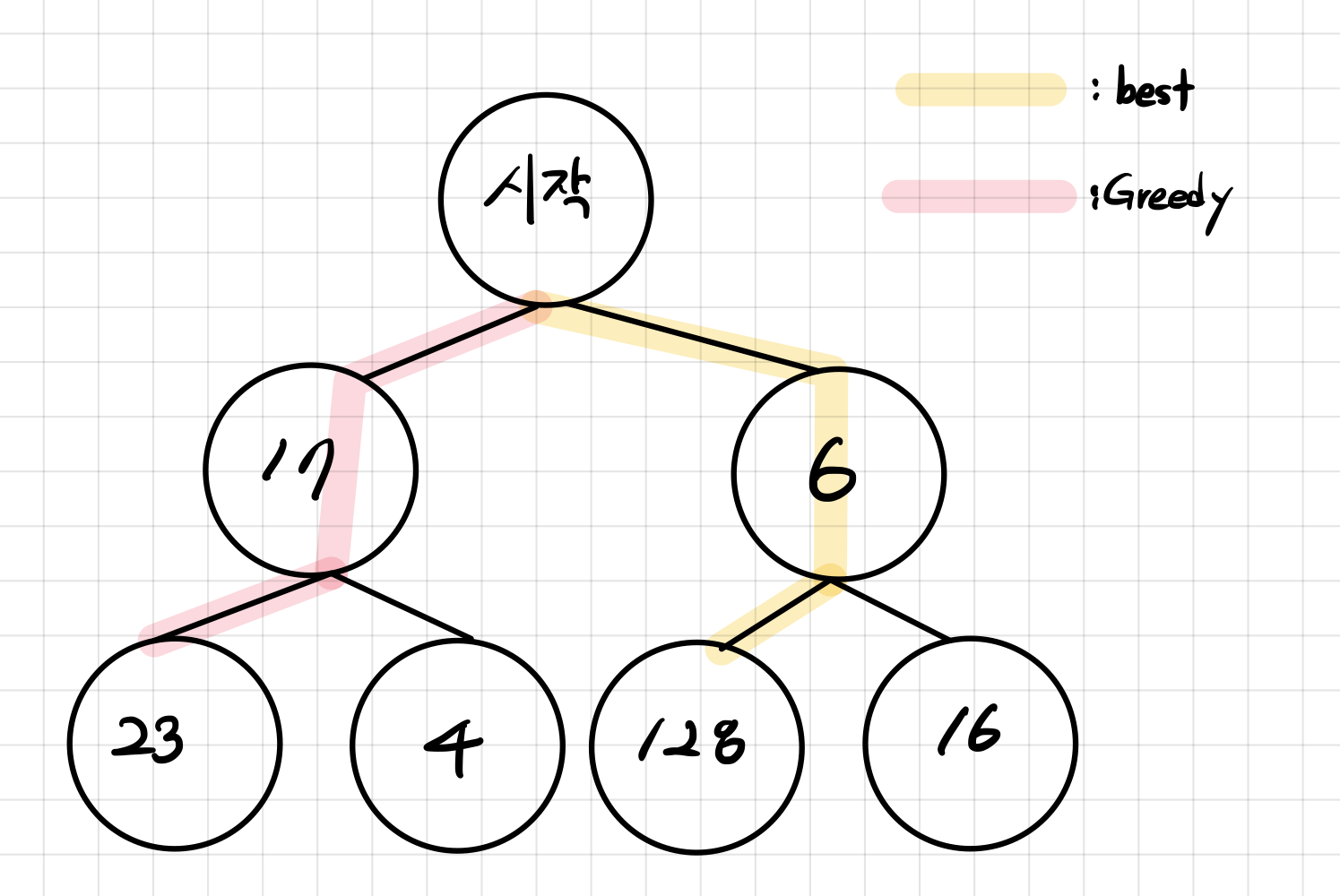
시작 지점에서부터 시작하여 가장 큰 수를 구하는 문제가 있다고 가정해봅시다.
우리는 가장 좋은 결과가 "시작 - 6 - 128"을 거치는 Path가 가장 큰 수를 도출할 수 있다는 것을 알 수 있습니다.
하지만 그리디 알고리즘을 사용한다면 시작 지점부터 가장 큰 수를 얻는 Path인 "17"을 선택하게 됩니다.
결론적으로는 그리디 알고리즘은 "시작 - 17 - 23" Path가 가장 좋은 것이라고 판단합니다.
이처럼 그리디 알고리즘은 현재 상황에서 가장 좋은 결과를 선택하는 방식입니다!
이러한 이유때문에 그리디 알고리즘을 사용하는 문제는 간단한 문제로 나올 가능성이 매우 크다고 할 수 있습니다.
그리디 알고리즘 조건
그리디 알고리즘을 사용하기 위해 필요한 조건은 2가지가 있습니다.
-
탐욕스러운 선택 조건
- 탐욕적인 선택은 항상 안전하다는 것이 보장되어야 합니다. 여기서 "안전하다"라는 것은 이 선택으로 인해 전체 문제의 최적해를 반드시 도출할 수 있어야 한다는 것입니다.위에서는 그리디 알고리즘을 사용해 결과 도출 시 최적해가 무조건 나오지 않는다고 하지 않았나요??
그리디 알고리즘을 사용하면 무조건 최적해가 나오는 것은 아닙니다! 하지만 그리디 알고리즘을 사용해 푸는 문제가 나왔을 때 이 조건이 만족되는가? 를 생각해 충족되면 그리디 알고리즘을 사용하는 것입니다.
즉, 그리디 알고리즘을 사용하면 최적해가 나올 수 있는 문제이여야 합니다. -
최적 부분 구조 조건
- 문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적의 해결 방법이다라는 조건입니다.
이 말은 전체 문제의 안에는 여러 단계가 존재하고, 이 여러 단계 내의 하나 하나의 단계에 대해 최적해가 도출되어야 한다는 것입니다.
그리디 알고리즘에서 고려해야 하는 상황은 값들이 서로 영향을 주면 안된다는 것을 염두에 두어야 합니다. 위에서 사용한 예시를 한번 더 사용해 설명해보겠습니다!
- 우선 그리디 알고리즘이 도출한 최종 Path는 "시작 - 17 - 23" 입니다.
이때 "6" 아래의 "128"이라는 값이 있어서 Path를 변경할 수 없다는 것입니다.
그리디 알고리즘 문제
가장 일반적인 문제의 예는 거스름돈 문제가 있습니다.
거스름돈 문제
당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한개 존재합니다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러주어야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.
이 문제에서 우리가 생각할 수 있는 것은 '가장 큰 단위의 돈부터 생각하자' 입니다. 만약 2240원이라는 돈을 거슬러 줘야 한다고 가정해봅시다.
이 돈을 거슬러 줄 수 있는 방법은 매우 많습니다. 10원만 사용해서 거슬러 줄 수도 있고, 다양한 동전을 사용하여 거슬러 줄 수 있지만, 조건에서는 '최소 개수'를 구하는 문제이므로 가장 큰 단위부터 거슬러주고 나머지를 그 다음 단위의 화폐로 거슬러 주는 것 이라는 해결 방법을 떠올릴 수 있습니다.
def solution(money):
answer = 0
change = [500, 100, 50, 10]
remain = money
for i in change:
answer += remain // i
remain = remain % i
return answer(이 문제는 파이썬을 사용해 풀었습니다.)
그리디 알고리즘을 사용해 답을 찾게 된다면, 그 답이 정당한지 생각해봐야 합니다.
거스름돈 문제는 가지고 있는 동전 중 '큰 단위'의 동전이 항상 '작은 단위'의 배수이므로(500원은 100원 5, 100원은 50원 2, 50원은 10원 * 5) 작은 단위 동전을 조합해 다른 해가 나올 수 없기 때문에 사용할 수 있습니다.
활동 선택 문제
이 문제는 시간표짜기, 회의실 시간 분배 문제와 비슷한 문제 유형에 해당합니다.
활동 선택 문제란, 한 강의실에서 여러개의 수업을 하려고 할 때 한번에 가장 많은 수업을 할 수 있는 경우를 고르는 것입니다. (수업 시작 시간, 수업 종료 시간)
- 조건으로는 시작 시간과 끝나는 시간이 같은 경우, 그것도 하나의 수업으로 쳐줍니다.(3 3, 5 5 등)
- 또 수업이 끝나고 바로 다른 수업을 시작할 수 있습니다. (1 3, 3 5, 5 7)
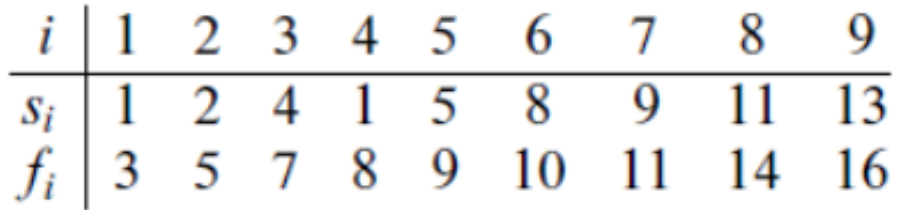

Si는 시작시간, Fi는 종료시간입니다. 수업들은 하나의 강의실에서 진행해야 하므로 2개의 수업이 중복해서 실행될 수 없습니다. 이 때 가장 많은 수업을 할 수 있는 경우를 찾아보세요.
(조합 중 가장 많은 수업을 고르는 것이지, 가장 많은 시간을 할 수 있는 경우를 조합하라는 것이 아닙니다)
-
이제 문제로 돌아와서 타임테이블을 보면 a1이 가장 빨리 끝나므로 선택합니다. 이 때 a2, a4는 시간이 겹치므로 고를 수 없습니다. 즉, 여기서 a2와 a4의 시작 시간(Si)가 a1의 종료 시간(Fi)보다 작으므로 고를 수 없다는 것을 알아야 합니다!
-
그다음 가장 빨리 끝나는 수업은 a3이고, 위와 같은 이유로 a5는 고를 수 없습니다.
-
이를 반복해보면 정답은 a1, a3, a6, a8 또는 a1, a3, a7, a8을 고를 수 있습니다.
-
최적해를 구하기 위해서는 가장 빨리 끝나는 수업을 골라야 합니다. 현재 상태에서 가장 빨리 끝나는 수업이 일찍 끝나게 되면 다음 단계에서 더 많은 활동을 구할 수 있기 때문입니다.
(이 단계를 수행하기 전에 활동에 대한 시간 배열을 Fi 기준으로 오름차순 정렬을 하였습니다.)
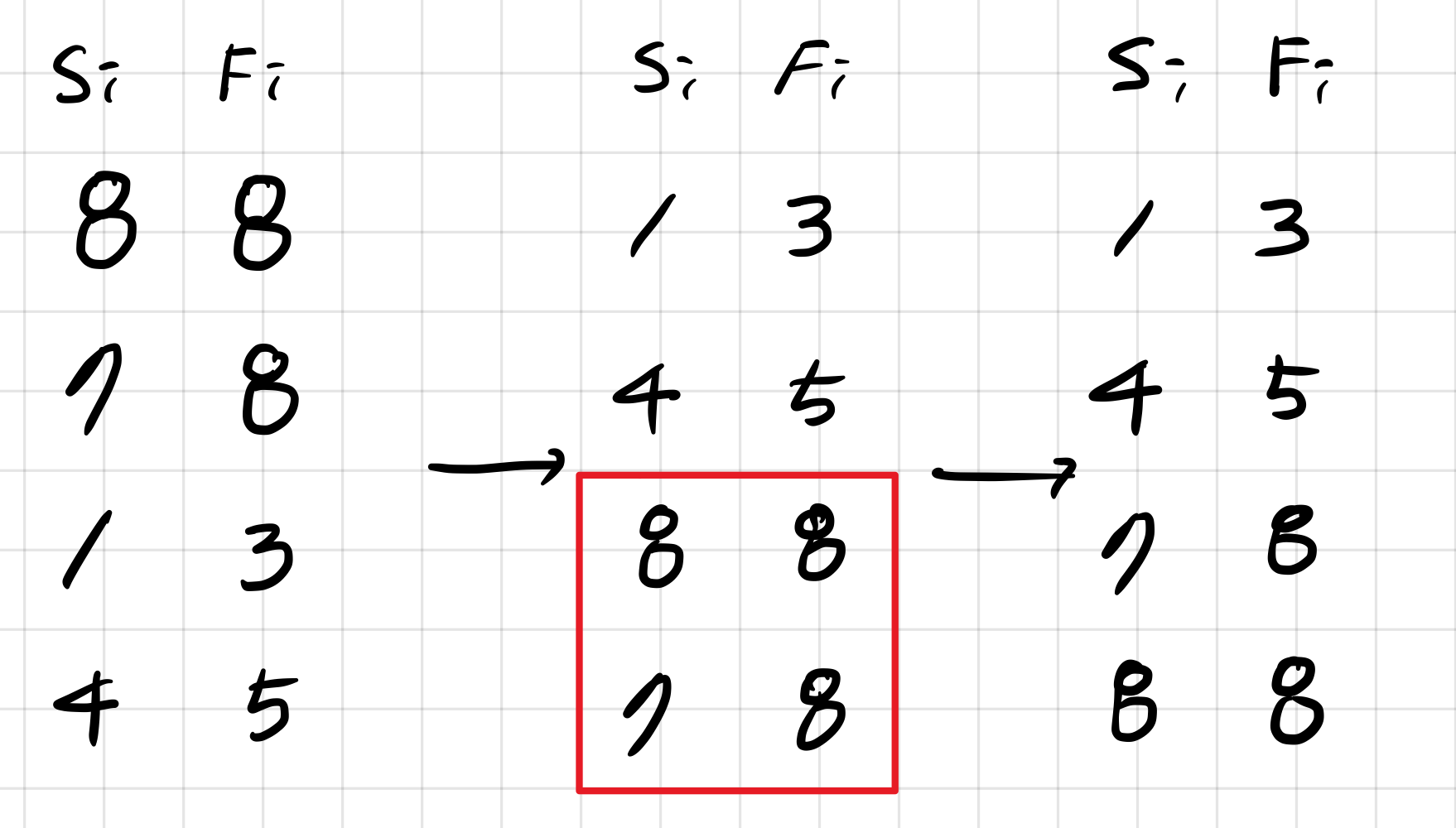
위의 예시는 Fi기준 정렬만 수행한 것입니다.예시에서 Fi 기준으로 오름차순 정렬을 실행하여 그리디 알고리즘을 사용한다면 결과는 (1 3) -> (4 5) -> (8 8)을 도출하게 됩니다. 정작 최적해는 (1 3) -> (4 5) -> (7 8) -> (8 8) 인데 말이죠!!
그래서 이를 방지하기 위해 Fi 기준으로 오름차순 정렬을 한 후 Si로 정렬을 합니다. 파이썬에서는 이러한 정렬을 편리하게 할 수 있는 내부 함수가 있습니다!!
(문제는 https://www.acmicpc.net/problem/1931 을 풀었습니다. 위 설명한 문제와 다르지만 방향은 같으므로 참고해주시길 바랍니다.)
n = int(input())
time_list = []
last_idx = 0
cnt = 0
for i in range(n):
time_list.append(list(map(int, input().split())))
time_list.sort(key=lambda x: (x[1], x[0])) # Fi 기준 정렬 후 Si 기준 정렬
for i in range(len(time_list)):
if time_list[i][0] >= last_idx:
last_idx = time_list[i][1]
cnt += 1
continue
else:
continue
print(cnt)참고 사이트
https://www.zerocho.com/category/Algorithm/post/584ba5c9580277001862f188
https://hevton.tistory.com/364
https://velog.io/@cyranocoding/동적-계획법Dynamic-Programming과-탐욕법Greedy-Algorithm-3yjyoohia5

그리디 알고리즘과 그 예시에 대해서 잘 알 수 있었습니다. 특히 그리디 알고리즘이 만족해야 할 조건을 잘 지키는 것이 굉장히 중요한데, 이런 부분에 대해서 예시를 잘 들어서 이해하기 쉽게 설명해준 것 같습니다. 좋은 포스팅 감사합니다!