오르막 수

오르막 수는 내부 숫자가 오름차순으로 이뤄져야 한다. 여기서 중요한 점은 아래와 같다.

1. 인접한 수가 같아도 오름차순이다.
2. 숫자는 0으로 시작할 수 있다.

그러므로 다음과 같은 수도 된다.
N이 2인 경우 00, 01도 되는 것이다.

해당 문제는 그림을 그리며 오르막 수가 될 수 있는 경우의 수를 나눠봤다.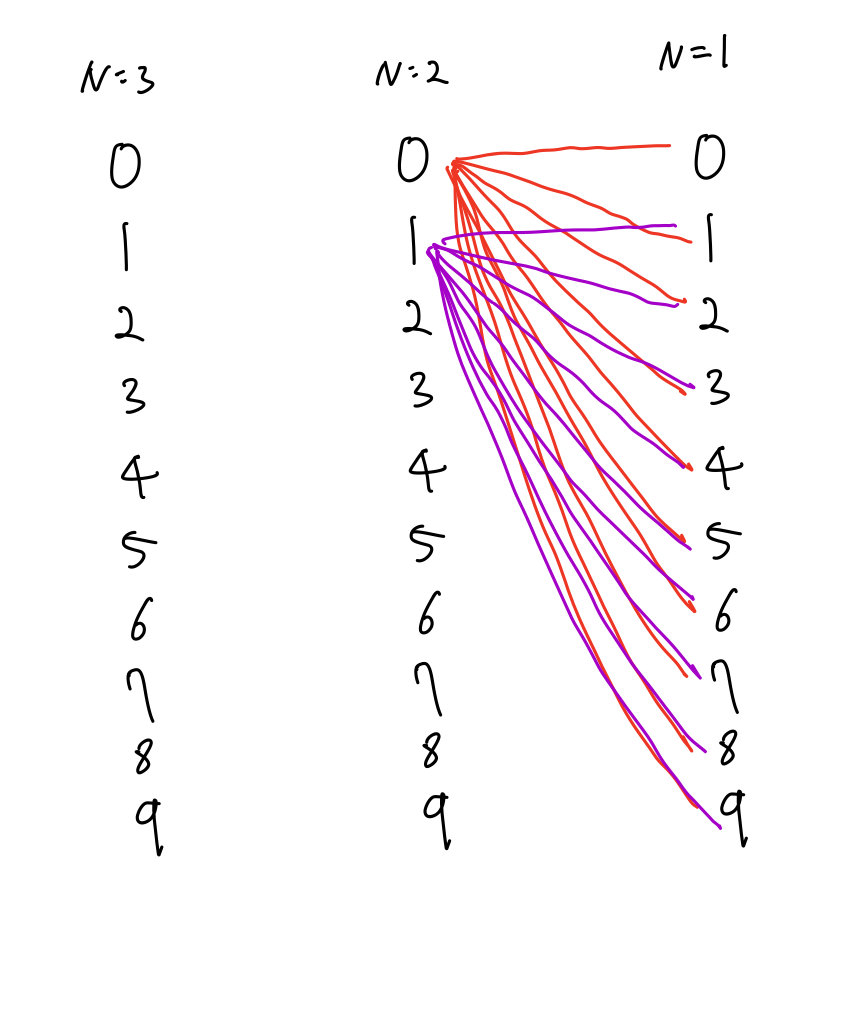

그리고 dp배열은 아래와 같이 정의를 했다.

dp[i][j]는 i자리의 수에 j로 시작하는 오르막 수의 개수

N이 1인 경우는 1자리의 수이다.
위 사진의 첫번째 N이 1이고 0으로 시작하는 경우 오르막 수의 개수는 1개이다.
N이 1인 경우는 모두 1개일 것이다. (이유는 1자리의 수에 0~9로 시작하는 수는 오르막 수의 개수는 1개이기 때문이다.)
그래서 dp[1][0~9]는 모두 1이다.

N이 2인 경우는 2자리의 수이다.
위 사진의 그림이 복잡해질까봐 dp[2][0], dp[2][1]만 표현을 했다.

dp[2][0]은 2자리 숫자에 0으로 시작하는 오르막 수의 개수이다.
이는 0뒤에 dp[1][0~9]를 더한 수와 같다.

dp[2][1]은 2자리 숫자에 1로 시작하는 오르막 수의 개수이다.
이는 1뒤에 dp[1][1~9]를 더한 수와 같다.
dp[1][1]~dp[1][9]를 더한 이유는 오르막 수를 유지하기 위해서이다.

N이 2인 경우만 봐도 N이 3인 경우는 똑같이 동작할 것이라는 것을 느낄 수 있다.
그래서 점화식은 아래와 같이 나타낼 수 있다.

dp[i][j] = dp[i-1][j]) + dp[i-1][j+1] + ... + dp[i-1][9]

그러므로 나는 소스코드를 다음과 같이 설계했다.

import sys

N = int(sys.stdin.readline().strip())
# dp[2][1]은 2자리의 숫자이면서 1로 시작하는 오르막 수의 개수, 첫번째 인덱스는 자리수, 두번째 인덱스는 오르막 수의 첫번째 숫자
dp = [[0] * 10 for _ in range(N + 1)]


for i in range(10):
    dp[1][i] = 1  # 0~9는 1로 초기화

for i in range(2, N + 1):
    for j in range(10):
        dp[i][j] = sum(dp[i-1][j:])  # i번째 자리수의 j로 시작하는 오르막 수는 i-1번째 자리수의 j부터 시작하는 오르막 수들의 총 합

print(sum(dp[N]) % 10007)