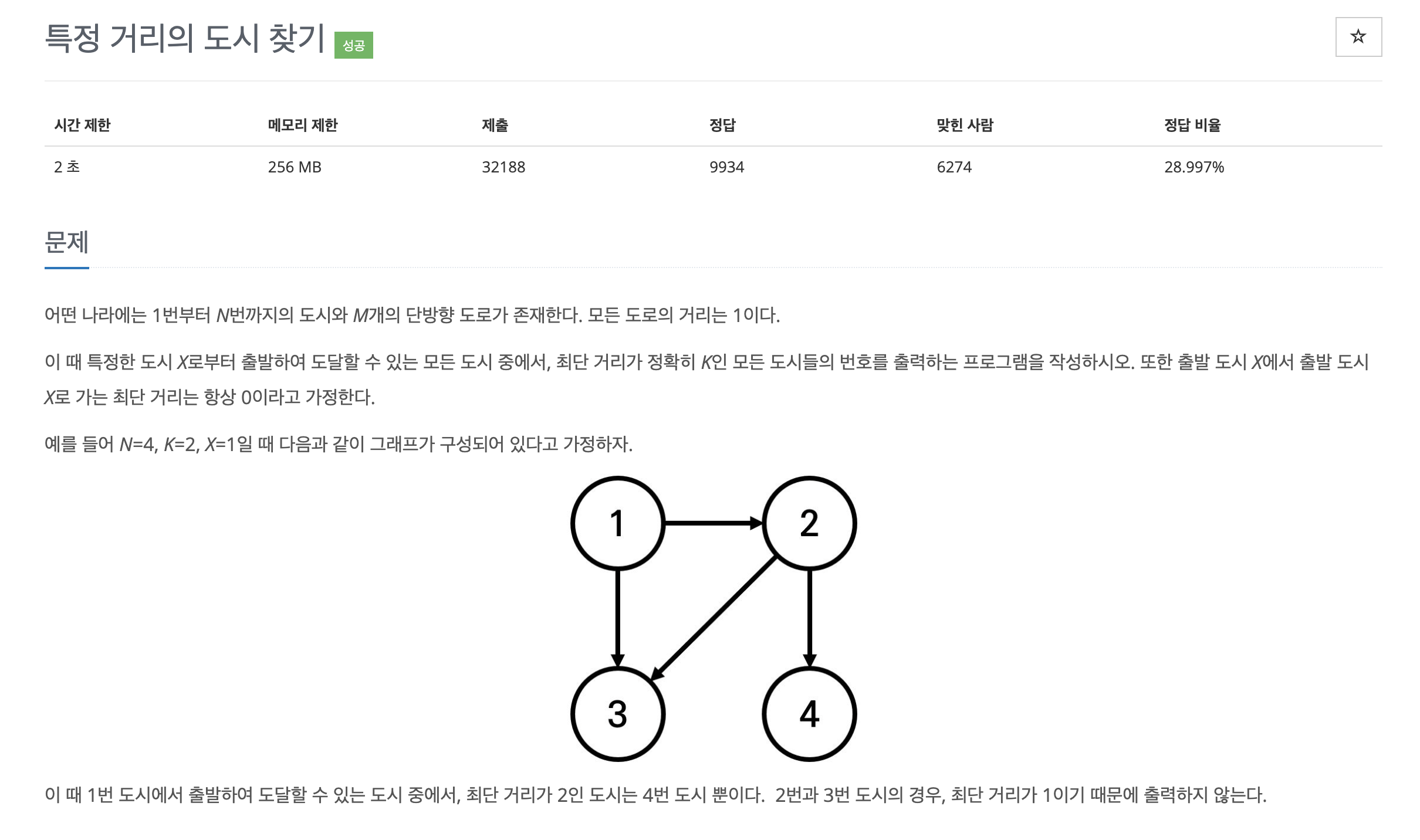
특정 거리의 도시 찾기

N개의 도시들이 있고, M개의 도로 개수가 있고, 출발 도시인 X에서, 최단거리가 K만큼 떨어진 도시를 찾으면 된다. 각 도시들의 거리는 1이다. 문제 조건을 보면 N은 300000개, 도로 개수는 1000000개이다. 시간 복잡도는 O(N+M)으로 동작하기 때문에 시간 초과 없이 해결이 가능하다. 이 문제는 BFS를 이용하여 해결을 할 예정이다. 출발 도시에 이어진 도시들을 queue에 넣고 난 뒤, 하나씩 queue에서 빼면서 최단거리를 저장하면 된다. 이 방법은 queue가 비었을 때까지 진행한다. 그래서 아래와 같은 코드가 나왔다.

 from collections import deque
import sys

n, m, k, x = map(int, sys.stdin.readline().strip().split())
graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b = map(int, sys.stdin.readline().strip().split())
    graph[a].append(b)  # 도로 정보 입력

distance = [-1]*(n+1)  # -1로 초기화
distance[x] = 0  # 출발 위치는 0으로 초기화

def bfs():
    queue = deque([x])  # x 값을 큐에 삽입

    while queue:
        now = queue.popleft()  # 큐에서 나온 데이터는 출발 도시

        for i in graph[now]:  # 출발 도시에서 연결되어있는 도시 찾기
            if distance[i] == -1:  # 방문하지 않은 도시인 경우
                distance[i] = distance[now]+1  # 거리 증가 시켜줌
                queue.append(i)  # 큐에 삽입

bfs()

if k not in distance:  # k만큼 떨어진 도시가 없는 경우
    print(-1)
else:  # k만큼 떨어진 도시가 있는 경우
    for i in range(1, n + 1):
        if distance[i] == k:
            print(i)