플로이드 워셜 알고리즘

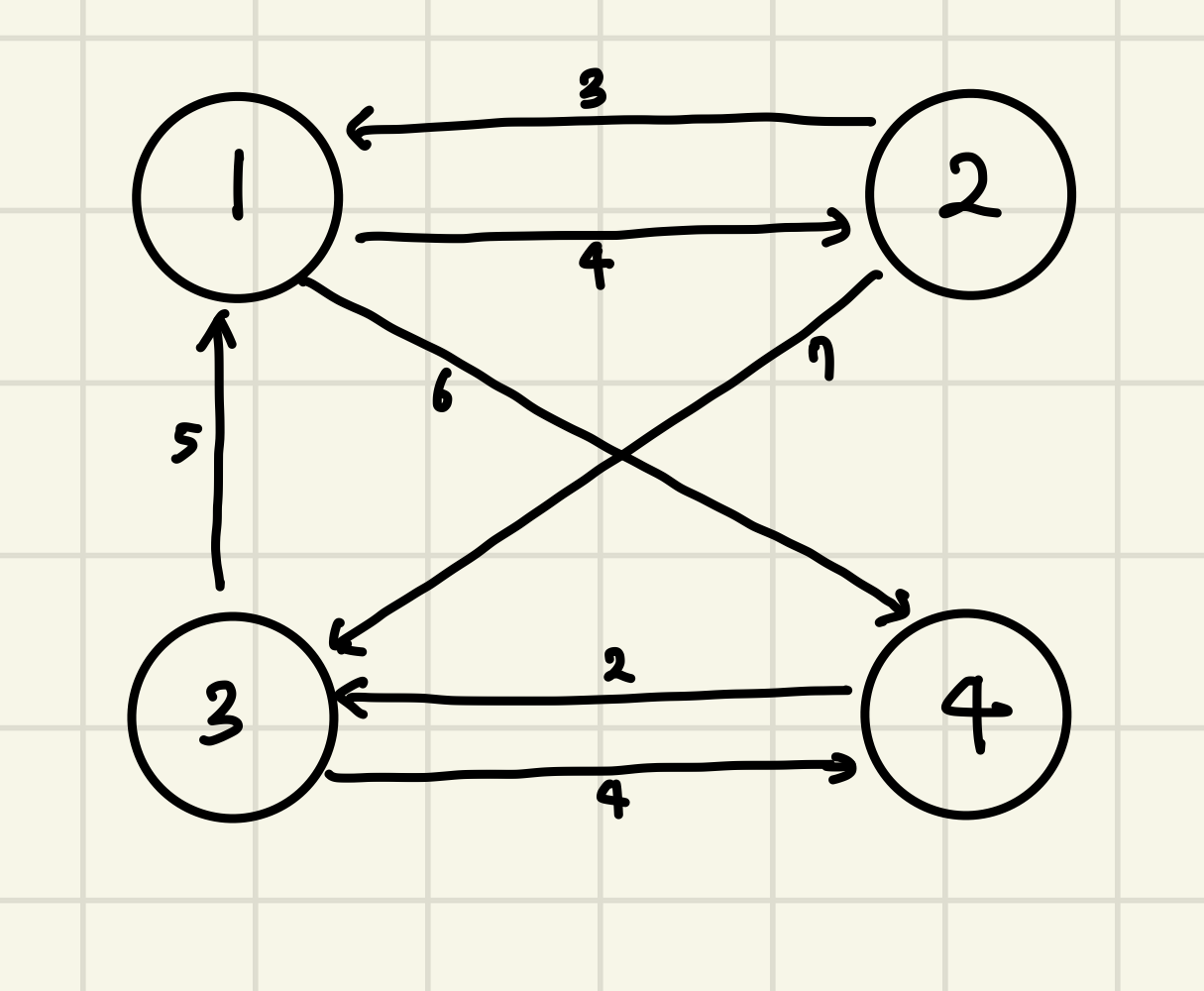
설명

다익스트라 알고리즘은 한 지점에서 다른 특정 지점까지의 최단 경로를 구해야하는 경우였다. 하지만 플로이드 워셜 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우에 사용할 수 있는 알고리즘이다. 다익스트라 알고리즘은 출발 노드가 1개이고 다른 모든 노드들의 거리를 저장하기엔 1차원 리스트를 사용했지만, 플로이드 워셜 알고리즘은 모든 지점에서 다른 지점까지의 최단 경로를 저장하기 때문에 2차원 리스트를 사용해야 한다. 플로이드 워셜 알고리즘은 어디를 거쳐 간다는 것이 가장 중요하다. 즉, 각 단계에서는 해당 노드를 거쳐가는 경우를 고려한다. 다익스트라는 그리디 알고리즘이라고 했지만, 플로이드 워셜 알고리즘은 거쳐가는 것을 고려하여 최단 거리를 출력하기 때문에 다이나믹 프로그래밍과 관련이 있다.

설명 예시

1번 노드에 대해서 확인할 때는 1번 노드를 중간에 거쳐 지나가는 모든 경우르 고려하면 된다. 즉, A -> 1번 노드 -> B로 가는 비용을 확인한 후에 최단 거리를 갱신한다. (A, B는 임의의 노드)

점화식

플로이드 워셜 알고리즘은 다이나믹 프로그래밍이므로 아래와 같은 점화식을 도출할 수 있다.

dp[a][b] = min(dp[a][b], dp[a][k] + dp[k][b])

소스코드

import sys

INF = int(1e9)

n = int(sys.stdin.readline().strip())
m = int(sys.stdin.readline().strip())

graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에게 가는 값은 0으로 초기화
for i in range(1, n + 1):
    for j in range(1, n + 1):
        if i == j:
            graph[i][j] = 0

for _ in range(m):
    # A에서 B로 가는 비용은 C
    a, b, c = map(int, sys.stdin.readline().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for i in range(1, n + 1):
        for j in range(1, n + 1):
            graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])

for i in range(1, n + 1):
    for j in range(1, n + 1):
        if graph[i][j] == INF:
            print("INFINITY", end=' ')
        else:
            print(graph[i][j], end=' ')
    print()

# 예제
# 4
# 7
# 1 2 4
# 1 4 6
# 2 1 3
# 2 3 7
# 3 1 5
# 3 4 4
# 4 3 2