프로그래머스 0단계 최빈값 구하기(for, if 문으로 풀기)

최빈값 구하기 문제는 인풋 배열에서 가장 자주 나오는 값을 구하는 문제입니다.

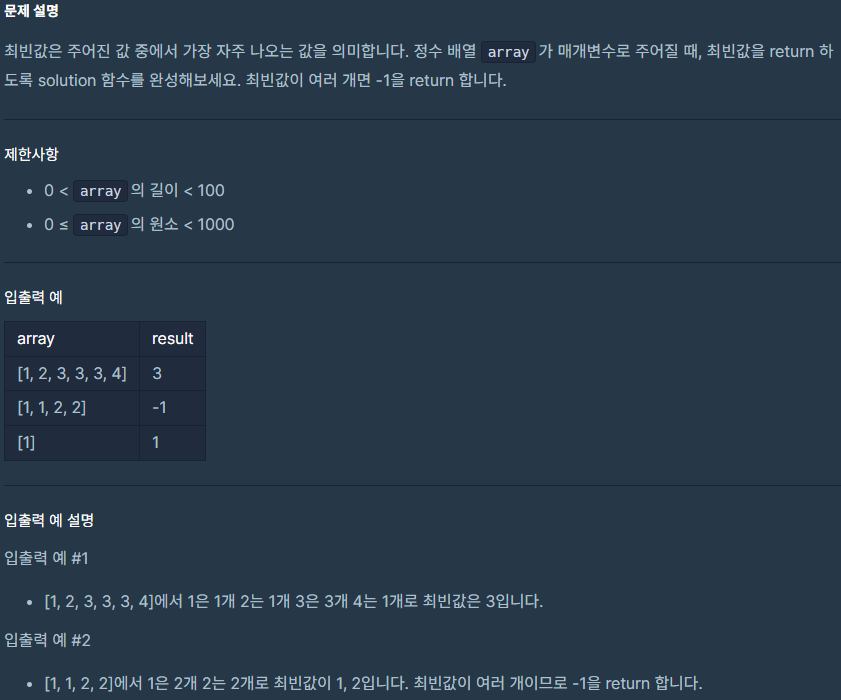
출처: https://school.programmers.co.kr/learn/courses/30/lessons/120812

이 문제는 자바 Collection 중 HashMap을 이용하여 푸는 문제입니다. 하지만, HashMap을 이용한 방법과 for, if 문으로 푸는 방법의 차이를 확인하고 왜 코딩테스트를 풀 때 효율적인 특정 방법을 떠올려서 문제를 풀어야 하는지 확인하고자 합니다.

for, if문으로 풀기 위해 먼저 특정 배열을 생성하려고 합니다. 여러 방법이 있겠지만 저는 최댓값을 구한 후에 그 크기를 갖는 배열을 생성하기 위해 최댓값을 구하는 함수를 생성했습니다.

public int maxNum(int[] arr) {
        int max = 0;
        int n = arr.length;

        for (int i = 0; i < n; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }

        return max;
    }

그 후 입력 배열의 원소를 인덱스로 하여 만들어진 배열의 값을 증가시켰습니다.

int max = maxNum(array);
        
int[] newArr = new int[max + 1];
        
for (int i = 0; i < n; i++) {
    newArr[array[i]]++;
}

밑의 통과한 코드를 보면 풀이를 위해 for문이 4번 사용됩니다. 다른 방법이 있겠지만 for문이 1번 사용되더라도 시간복잡도는 O(n)입니다.

빅 오 표기법에서는 상수는 무시하기 때문에 O(4n) = O(n)이다.

class Solution {
    public int solution(int[] array) {
        int answer = 0;
        int n = array.length;     
        
        if (n == 1) {
            answer = array[0];
        }
        
        int max = maxNum(array);
        
        int[] newArr = new int[max + 1];
        
        for (int i = 0; i < n; i++) {
            newArr[array[i]]++;
        }
        
        answer = maxNum(newArr);
        
        int cnt = 0;
        int temp = 0;
        
        for (int i = 0; i < newArr.length; i++) {
            if (newArr[i] == answer) {
                temp = i;
                cnt++;
            }
        }
        
        if (cnt != 1) {
            return -1;
        } else {
            return temp;
        }
    }
    
    
    public int maxNum(int[] arr) {
        int max = 0;
        int n = arr.length;
        
        for (int i = 0; i < n; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        
        return max;
    }
}

다음 글에서 정리하겠지만 HashMap의 시간복잡도는 O(1)입니다. 이 문제의 제한사항에 입력의 길이가 100보다 작기 때문에 이 풀이는 성능의 이슈없이 통과되었지만 n이 매우 커지면 O(1)과 O(n)의 차이는 매우 극심할 것입니다.