1. Lonely Photo (BOJ 23878번)

USACO 공식 풀이 링크

풀이 시간: 1시간 고민해서 못 풀었다.

$N\le500,000$ 이므로, 최소한 $O(N \log N)$의 최적화는 필요.
구간합 배열 풀이가 떠올랐으나, $O(N^2)$이라 포기.
투 포인터도 이용해보려 하였으나, 현재 외로운 사진이면 늘려도 줄여도 안 외로울 수 있기에 잘 되지 않았음.

---

정해는 $O(N)$ 풀이다.

각 소를 순회하며 Lonely Cow로 지정하고,
Lonely Cow 좌측/우측에 자기와 다른 종의 소가 몇마리까지 연속됐는지를 확인하고,
(좌측과 우측에 걸친 경우 + 좌측과 Lonely Cow까지 + Lonely Cow부터 우측까지) 의 Lonely Photo의 수를 세 주면 된다.

한 마리 셀 때마다 최대 $N$개까지 왼쪽 오른쪽으로 늘릴 수 있는데,
$N$마리 모두를 그렇게 세야 하니 $O(N^2)$ 아닌가? 싶지만,
놀랍게도 실제로 손으로 풀어보면 각 소가 아래 그림처럼 2번까지만 세진다. 고로 $O(N)$.

정답 코드: $O(N)$

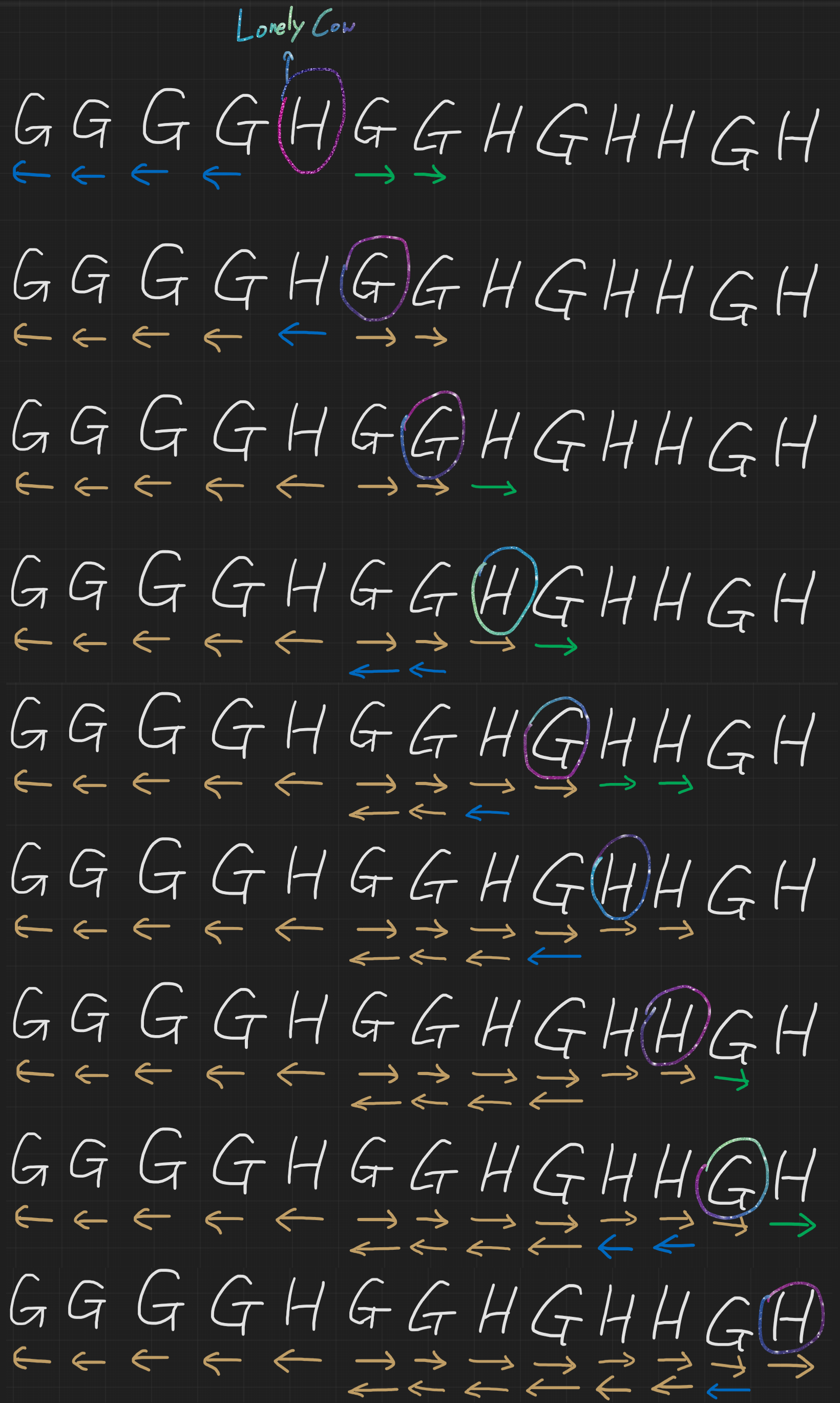
using ll = long long;

int main()
{
    int N;  string str;
    cin >> N >> str;

    ll lonely = 0;
    for (int i = 0; i < N; ++i)
    {
        // 연속된 Lonely Cow와 다른 종류의 소를 좌우로 센다.
        ll lCnt = 0, rCnt = 0;
        for (int k = i - 1; k >= 0 && str[k] != str[i]; --k)
            ++lCnt;
        for (int k = i + 1; k < N && str[k] != str[i]; ++k)
            ++rCnt;
        // 좌측과 우측에 걸친 사진 개수
        lonely += lCnt * rCnt;
        // 좌측과 Lonely Cow까지의 사진 개수
        lonely += max(0LL, lCnt - 1);
        // Lonely Cow와 우측까지의 사진 개수
        lonely += max(0LL, rCnt - 1);
    }
    cout << lonely;
}

2. Air Cownditioning (BOJ 23879번)

USACO 공식 풀이 링크

풀이 시간: 56분 (그렇지만, $O(NT)$ 풀이가 데이터가 약해서 통과된거라, 사실상 틀림.)

내 느린 풀이는 앞에서부터 보면서 증감시켜야 하는 연속된 cluster를 찾은 다음,
해당 cluster의 절댓값의 최솟값만큼 증감시키는 것을 반복하는 그리디 풀이였음.

최대 온도차를 $T$라 하면 $T \le 10,000$ 이고 $N \le 100,000$ 인데
$O(NT)$ 풀이라서 시간 초과돼야 정상이지만, 데이터가 약해서 통과되었다.

---

정해는 $O(N)$ 풀이다.

우선, 온도 차이만이 중요하므로 입력으로 받는 두 배열을 빼서 temper[N] 배열로 저장해놓자.
그리고 이 temper[N] 배열의 모든 원소가 0이 되도록 온도조절기를 돌리면 될 것이다.

이 때, temper의 인접한 원소간의 차이(절댓값)를 저장하는 diff[N+1]을 만들어보면,
$[i,j]$ 구간에 온도조절기를 가동할 때마다 diff[i-1]와 diff[j]만이 1씩 줄어드는 것을 알 수 있다.
(temper[N] 처음과 끝에 dummy 원소 0이 하나씩 더 있다고 가정했다.)

dummy 원소까지 포함해 모든 diff[i]를 0으로 만들었을 때에만 모든 temper[i]도 0이 된다.

매 온도조절기 가동마다 diff의 원소 중 2개가 1씩 줄어드므로, 총 2가 줄어든다.
그러므로, (모든 diff의 원소들의 합) / 2 가 온도조절기 가동 횟수임을 알 수 있다.

정답 코드: $O(N)$

int main()
{
    int N;  cin >> N;
    // 온도 차이를 저장하는 배열
    // (인덱스 0과 N+1은 dummy로, 값은 0)
    vector<int> temper(N + 2, 0);
    for (int i = 1; i <= N; ++i)
        cin >> temper[i];
    for (int i = 1; i <= N; ++i)
    {
        int dt;  cin >> dt;
        temper[i] -= dt;
    }

    // temper의 인접 원소의 차이를 저장하는 배열
    vector<int> diff(N + 1);
    for (int i = 0; i <= N; ++i)
        diff[i] = abs(temper[i + 1] - temper[i]);

    // 모든 diff의 원소의 합 / 2 하면 온도조절기 가동 횟수
    int sum = 0;
    for (int d : diff)
        sum += d;
    cout << sum / 2;
}

3. Walking Home (BOJ 23880번)

USACO 공식 풀이 링크

풀이 시간: 54분 ($O(TN^3)$ 브루트 포스로 풀었는데, USACO 공홈에서는 마지막 테케 시간 초과)

USACO 공식 풀이는 $K\ge1, K\ge2, K\ge3$ 인 각 경우를 나눠서 3중 반복문을 돌렸다. $O(TN^3)$
그런데 이건 $K\ge4, K\ge5, ...$ 인 경우는 계속 추가로 코딩해야 하는 풀이이므로, 내 풀이를 소개하겠다.

내 풀이($O(TN^3)$)를 요약하면, 주변 칸으로 이동할 수 있는지 매번 판단하고,
이동 가능하다면 재귀호출로 한 칸 이동하는 백트래킹 풀이이다.
그렇게 계속 이동하다가 헛간에 무사히 도착하면 경로의 개수를 1 늘리는 식이다.

일단, 이동 범위를 보드판 안쪽으로 제한해보자.
보드판의 크기가 $5 \times 5$ 이라 하면, 오른쪽($R$)으로 $4$번, 아래쪽($D$)으로 $4$번 이동해야 목적지에 도착할 것이다.
예를 들어, $DRRRDDDR$ 식으로 $3$번 방향을 바꾼 경로가 존재할 수 있다.
(물론, 중간에 건초더미를 만나는 경로라면 제외해야 할 것이다.)

이렇게, $D$와 $R$을 적절한 순서로 배치한다고 생각하면,
남은 $D$와 $R$의 수를 매개변수로 하여 재귀함수를 계속 호출하는 풀이를 떠올릴 수 있다.

void backtrack(int remainR, int remainD, ...)

이 풀이에서 어려운 점은 이동 가능한지 판단하기가 다소 복잡하다는 것이다.
예를 들어, 우측($R$)으로 이동 가능한지 판단해보자.

1. remainR > 0 이어야 한다.
2. 이동할 칸에 건초 더미가 없어야 한다.
3. 직전에 이미 우측으로 이동 중이었다면, 방향 전환 횟수를 소모하지 않지만,
   직전에 우측 이동이 아니었다면, 방향 전환 횟수가 남아있어야 한다.

이런 조건을 표현하기 위해서는, 현재 위치(curPos), 직전 이동 방향(prevDir), 남은 방향 전환 횟수(remainTurn)의 3개의 매개변수를 추가해야한다.

struct Pos { int y, x; };
enum class Dir { NONE, RIGHT, DOWN };

char board[50][51];

void backtrack(int remainR, int remainD, Dir prevDir, int remainTurn, Pos curPos)
{
    ...
    // 오른쪽으로 갈 수 있으면 오른쪽으로 진행
    Pos candi{ curPos.y, curPos.x + 1 };
    if (remainR > 0 && board[candi.y][candi.x] != 'H' && (prevDir == Dir::RIGHT || remainTurn > 0))
    {
        // 방향 전환을 했으면 횟수 -1, 아니면 그대로
        const int newRemainTurn = (prevDir != Dir::RIGHT) ? remainTurn - 1 : remainTurn;
        backtrack(remainR - 1, remainD, Dir::RIGHT, newRemainTurn, candi);
    }
    
    // 아래쪽으로 갈 수 있으면 아래쪽으로 진행
    ...
}

아래쪽 이동도 비슷하게 추가하면 된다.

마지막으로, 헛간에 도착하는 경우 answer의 개수를 1 늘려주고 재귀호출을 멈춘다.

int N;
int answer = 0;

void backtrack(int remainR, int remainD, Dir prevDir, int remainTurn, Pos curPos)
{
    // 헛간에 도달했으면 답안으로 처리
    if (curPos.y == N - 1 && curPos.x == N - 1)
    {
        ++answer;
        return;
    }
    ...
}

맨 처음 출발할 때는 prevDir이 없으므로, prevDir = Dir::NONE 으로 세팅하고,
첫 이동도 방향 전환 취급해서, 방향 전환 횟수를 1 추가해서 백트래킹을 시작하면 된다.

// 첫 시작도 방향 전환으로 취급하고 방향 전환 횟수를 K+1 로 취급
backtrack(N - 1, N - 1, Dir::NONE, K + 1, { 0, 0 });

$2N-2$칸을 이동해야 헛간에 도착하는데, 방향 전환을 중간에 최대 $3$번까지 할 수 있다.
출발 방향이 $2$가지고, 각 출발 방향에 대해 언제 방향 전환할지를 선택하는 경우의 수를 따져야 하므로
테케당 총 경우의 수는 $2\sum\limits_{i=1}^{3}{}_{2N-2} C_i=O(N^3)$ 가지이다.
부분 정답 코드: $O(TN^3)$

---

사실 USACO 공식 풀이 제일 아랫줄에 보면 $O(TN^2K)$가 가능하지만 난도상 다루진 않겠다고 짧게 언급한다.

솔브드 난도를 보니 4차원 DP를 어떻게 잘 활용하면 가능한 것 같은데...
급 귀찮아져서 나중에 이 글 수정해서 추가해야겠다.