10. Array Partition I

리트코드

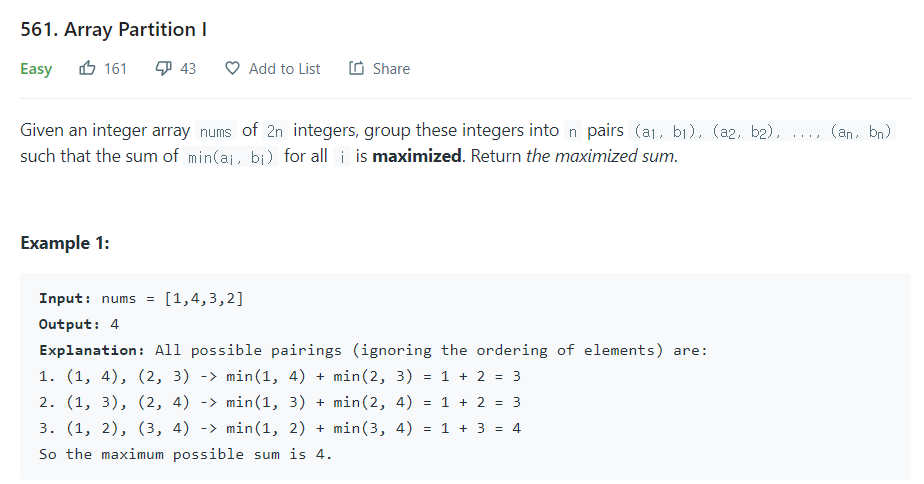
• n개의 페어를 이용한 min(a,b)의 합으로 만들 수 있는 가장 큰 수를 출력하라

1. 오름차순 풀이 (332ms)

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        pair = []
        nums.sort()
        
        for n in nums:
            # 앞에서부터 오름차순으로 페어를 만들어서 합 계산
            pair.append(n)
            if len(pair) == 2:
                sum += min(pair)
                pair = []
                
        return sum

• 페어의 min()을 합산했을 때 최대(Argmax)를 만드는 것은 결국 min()이 되도록 커야 한다는 것이고, 뒤에서부터 내림차순(Descending Order)으로 집어넣으면 항상 최대 min() 페어를 유지할 수 있다.

• 배열 입력 값은 항상 2n개일 것이므로 앞에서부터 오름차순(Ascending Order)으로 집어넣어도 결과는 같을 것이다.

• 정렬된 상태에서 앞에서부터 오름차순으로 인접 요소 페어 (Adjacent Elements Pair) 를 만들면 가장 큰 a1과 a2페어들을 만들 수 있고 이 페어들의 합이 곧 만들 수 잇는 최대 합니 된다.

• 예:

  1. min(1,4) + min(2,3) = 3
  2. min(1,3) + min(2,4) = 3
  3. min(1,2) + min(3,4) = 4

  
  
  

2. 짝수 번째 값 계산 (308ms)

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        nums.sort()
        
        for i, n in enumerate(nums):
            #짝수 번째 값의 합 계산 (인덱스가 짝수)
            if i % 2 == 0:
                sum += n
                
        return sum
         
         

• 이렇게 페어에 대해 일일이 min() 값을 구하지 않아도 짝수 번째 값(0부터 시작하므로)을 더하면 될 것 같다.

• 정렬된 상태에서는 짝수 번째에 항상 작은 값이 위치하기 때문이다.

• 불필요한 리스트 변수를 생략할 수 있기 때문에, 전체 코드 또한 많이 줄어들어 매우 간결하게 구현할 수 있다.

3. 파이썬 다운 방식 (284ms)

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        nums.sort()
        
        for i, n in enumerate(nums):
            #짝수 번째 값의 합 계산 (인덱스가 짝수)
            if i % 2 == 0:
                sum += n
                
        return sum
         

• 슬라이싱 구문을 활용하면 단 할 줄로도 풀이가 가능하다.

• [::2]는 2칸씩 건너 뛰므로 작수 번째를 계산하는 것과 동일하다.