101. 미로 탈출

• 동빈이는 N X M 크기의 직사각형 형태의 미로에 같혀 있다. 미로에는 여러마리의 괴물이 있어 이를 피해 탈출해야 한다.

• 동빈이의 위치는 (1, 1)이고 미로의 출구는 (N, M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있다.

  • 이때 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있다.

• 미로는 반드시 탈출할 수 있는 형태로 제시된다.

• 동빈이가 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하시오.

  • 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산한다.

• 입력조건

  • 첫째 줄에 두 정수 N, M (4 ≤ N, M ≤ 200)이 주어집니다.

    다음 N개의 줄에는 각각 M개의 정수 (0 혹은 1)로 미로의 정보가 주어진다.

    • 각각의 수들은 공백 없이 붙어서 입력으로 제시된다.

    • 또한 시작 칸과 마지막 칸은 항상 1이다.

• 출력조건

  • 첫째 줄에 최소 이동 칸의 개수를 출력하라

1. BFS를 이용한 풀이

import time
from collections import deque

n, m = map(int, input().split())

#2차원 리스트의 맵 정보 입력받기
graph = []
for i in range(n):
  graph.append(list(map(int, input())))

print(graph)


start = time.time()


#이동할 방향 정의 (상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]

def bfs(x, y):
  #큐 구현을 위해 deque 라이브러리 사용
  queue = deque()
  queue.append((x,y))
  #큐가 빌 때까지 반복
  while queue:
    x, y = queue.popleft()
    #현재 위치에서 네 방향으로의 위치 확인
    for i in range(4):
      nx = x + dx[i]
      ny = y + dy[i]

      #미로 찾기 공간을 벗어난 경우 무시
      if nx < 0 or ny < 0 or nx >= n or ny >= m:
        continue

      #벽인 경우 무시
      if graph[nx][ny] == 0:
        continue
      
      #해당 노드를 처음 방문하는 경우에만 최단 거리 기록
      if graph[nx][ny] == 1:
        graph[nx][ny] = graph[x][y] + 1
        queue.append((nx, ny))

  #가장 오른쪽 아래까지의 최단 거리 반환
  return graph[n-1][m-1]

print(bfs(0,0))

 
print(time.time()-start)

• 이 문제는 BFS를 이용했을 때 매우 효과적으로 해결할 수 있다.

  • BFS는 시작 지점에서 가까운 노드부터 차례대로 그래프의 모든 노드를 탐색하기 때문이다.

  • (1, 1) 지점에서부터 BFS를 수행하여 모든 노드의 값을 거리 정보로 넣으면 된다.

• 특정한 노드를 방문하면 그 이전 노드의 거리에 1을 더한 값을 리스트에 넣는다.

• 예를 들어 만약 미로의 크기가 3 X 3인 미로가 있다고 가정하면 다음과 같이 수행된다.

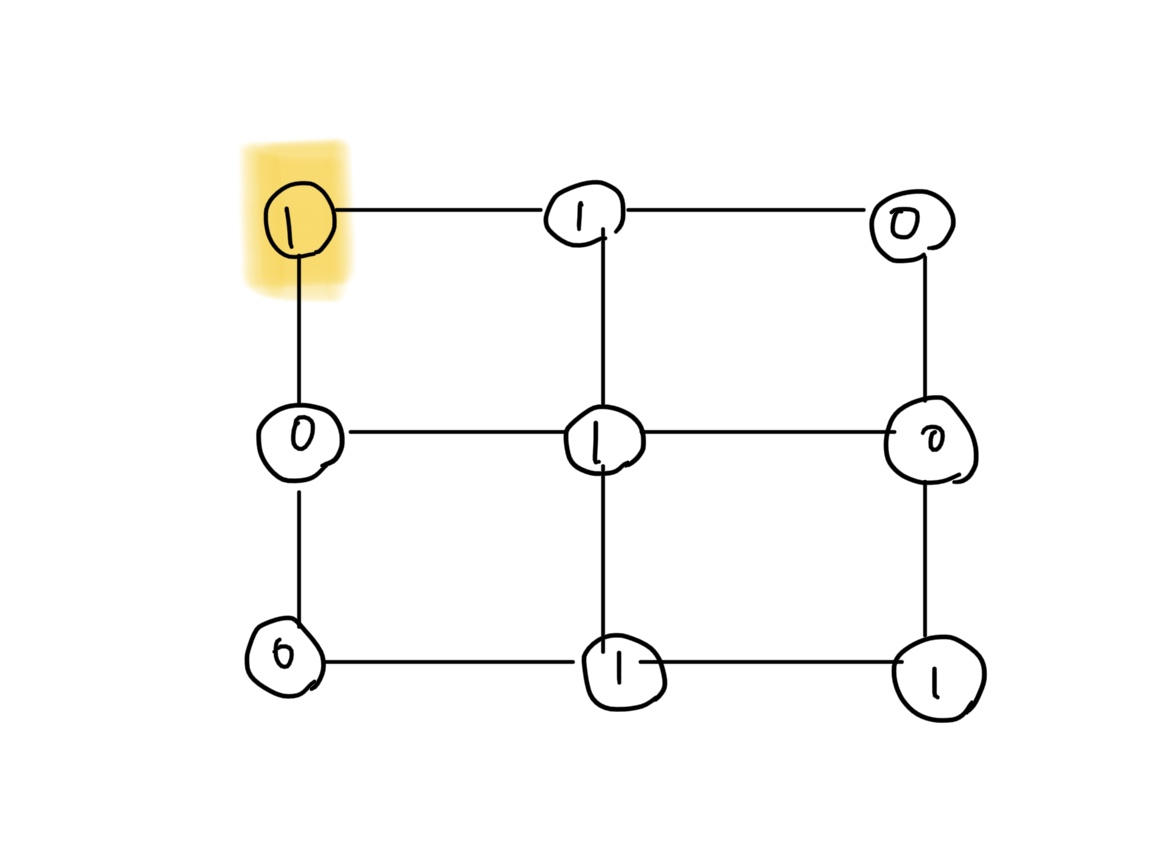
  1. 맨 처음에 (1, 1)의 위치에서 시작하며, (1, 1)의 값은 항상 1이라고 문제에서 언급되어 있다.

  

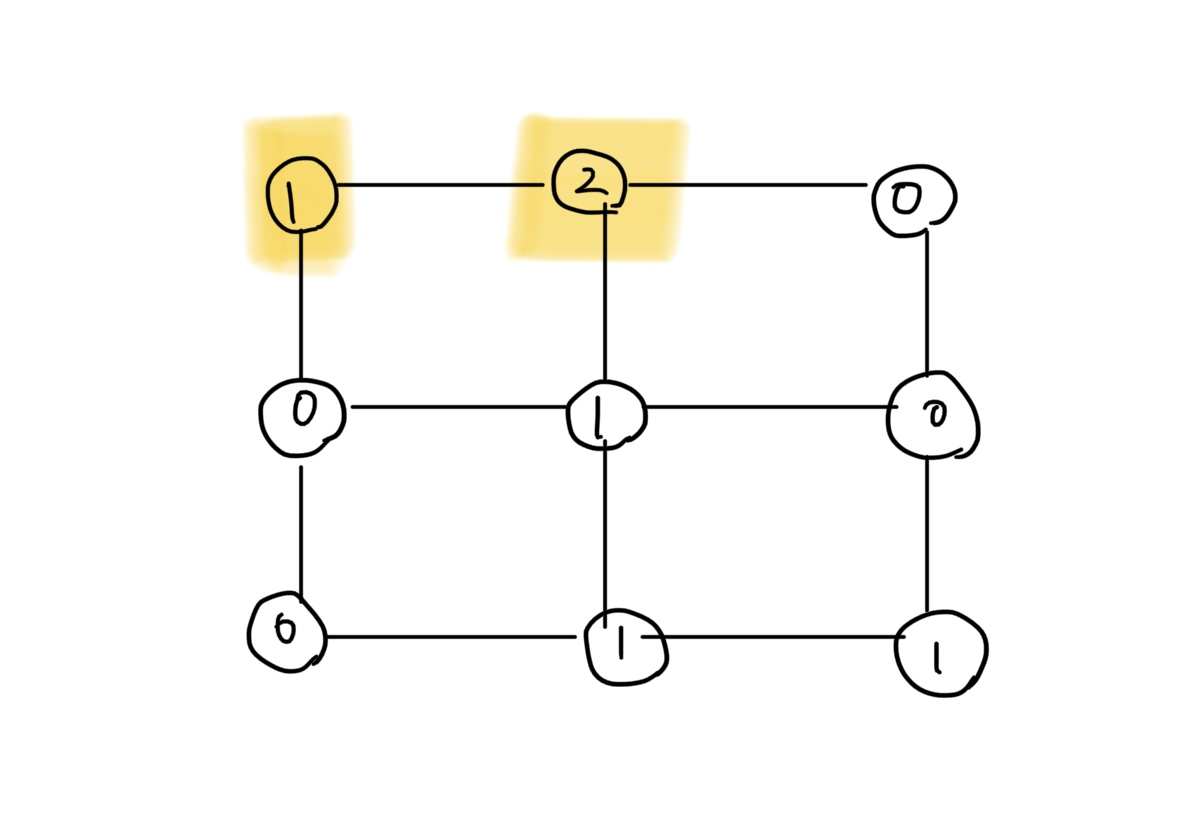
  2. (1, 1) 좌표에서 상, 하, 좌, 우로 탐색을 진행하면 바로 옆 노드인 (1, 2) 위치의 노드를 방문하게되고 새롭게 방문하는 (1, 2) 노드의 값을 2로 바꾸게 된다.

  

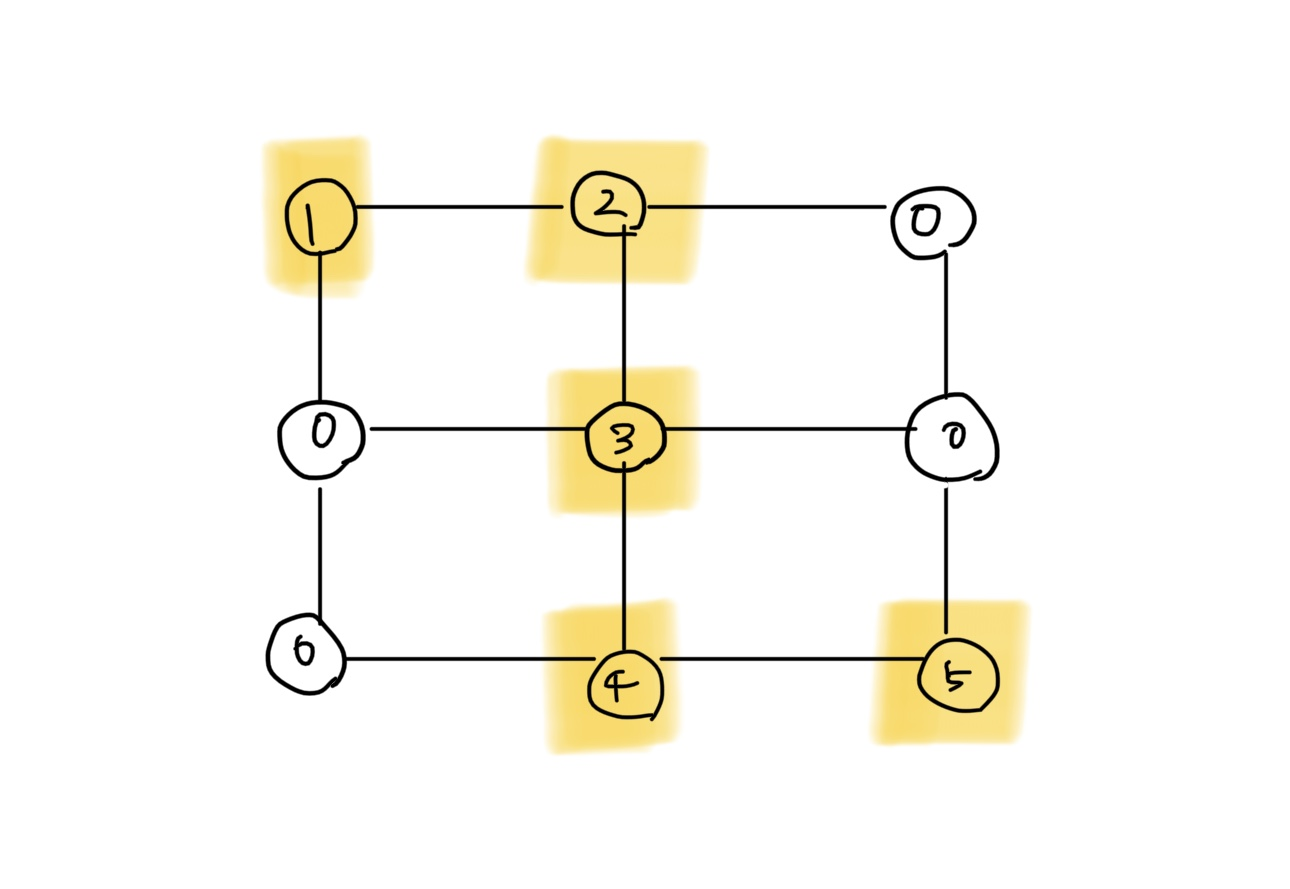
  3. 마찬가리로 BFS를 계속 수행하면 결과적으로 다음과 같이 최단 경로의 값들이 1씩 증가하는 형태로 변경된다.

  

• 소스코드에서 첫번째 시작 위치는 다시 방문할 수 있도록 되어 첫 번째 시작 위치 해당하는 값이 3으로 변경될 여지가 있다.

  • 여기서는 가장 오른쪽 아래 위치로 이동하는 것을 요구하고 있기에 괜찮다.